1.
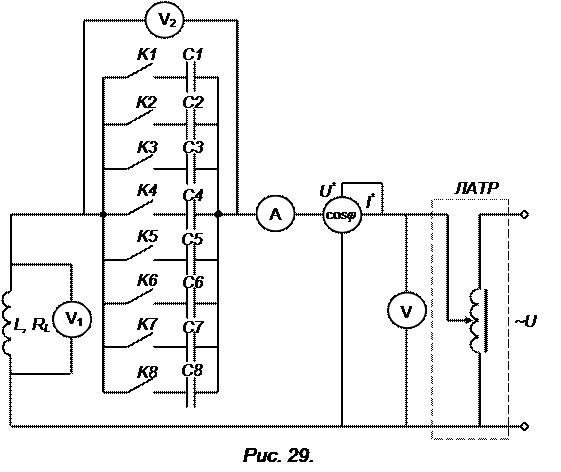 |
Собрать на лабораторном стенде схему исследуемой цепи (рис. 29).
2. Включить в цепь, замкнув на стенде контакт К4, минимальную ёмкость (С = 2 мкФ) батареи конденсаторов.
3. Подать на вход цепи с помощью лабораторного автотрансформатора (ЛАТР а) напряжение U = 40 В.
4. Поддерживая неизменным входное напряжение, увеличивать ёмкость батареи конденсаторов на 2 мкФ до максимального значения (34 мкФ). При этом измеренные в каждом случае значения тока, напряжения и коэффициента мощности занести в таблицу 3.
Таблица 3.
| Номер ступени батареи конденсаторов | Ёмкость батареи конденсаторов, мкФ | I, A | U, В | URL, В | UC, В | cos φ |
5. По данным таблицы 3 построить графики зависимостей
I = f(C), UC = f(C), URL = f(C)
6. По данным эксперимента построить в выбранных масштабах векторные диаграммы для трёх состояний цепи – до резонанса, близкого к резонансу и после резонанса.
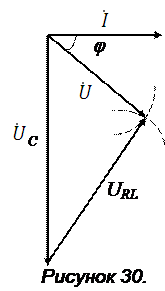 Примечание. Построение векторной диаграммы для неразветвлённой цепи удобнее начинать с вектора тока
Примечание. Построение векторной диаграммы для неразветвлённой цепи удобнее начинать с вектора тока 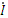 , который одинаков во всех участках. Затем из начала вектора
, который одинаков во всех участках. Затем из начала вектора 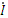 под углом 90° по ходу часовой стрелки откладывают вектор
под углом 90° по ходу часовой стрелки откладывают вектор  (т.к. напряжение на конденсаторе отстаёт от тока на четверть периода:
(т.к. напряжение на конденсаторе отстаёт от тока на четверть периода:  ). Напряжение
). Напряжение 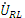 на катушке индуктивности опережает ток на угол
на катушке индуктивности опережает ток на угол  . Но так как величина этого угла в нашем случае не известна, то исходя из того, что согласно второму закону Кирхгофа
. Но так как величина этого угла в нашем случае не известна, то исходя из того, что согласно второму закону Кирхгофа  (т.е. векторы
(т.е. векторы  ,
, 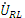 и
и 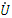 образуют треугольник напряжений), положение векторов
образуют треугольник напряжений), положение векторов 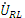 и
и 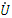 определяют методом засечек (рисунок 30).
определяют методом засечек (рисунок 30).
Очевидно, что до резонанса 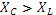 , следовательно,
, следовательно,  и
и  , т.е. напряжение
, т.е. напряжение 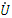 на входе цепи отстаёт от тока
на входе цепи отстаёт от тока 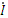 . В резонансе
. В резонансе  ,
,  и
и  , т.е. напряжение
, т.е. напряжение 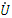 и ток
и ток 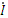 на входе цепи синфазны. После резонанса
на входе цепи синфазны. После резонанса 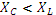 ,
,  ,
,  и напряжение
и напряжение 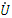 опережает ток
опережает ток 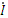 .
.
Содержание отчёта.
1. Схема исследуемой электрической цепи (рисунок 29).
2. Таблица измеренных величин (таблица 3).
3. Графики зависимостей I = f(C), UC = f(C), URL = f(C).
4. Векторные диаграммы для трёх состояний цепи – до резонанса, близкого к резонансу и после резонанса.
Контрольные вопросы.
1. Дайте определение электрического резонанса.
2. В каких цепях можно наблюдать резонанс напряжений и каково условие его возникновения?
3. Как практически можно добиться резонанса напряжений?
4. Назовите основные признаки резонанса напряжений.
5. Поясните, почему при резонансе напряжений ток в цепи принимает максимальное значение?
6. Почему состояние резонанса напряжений является опасным, и какие его особенности используются в технике?
Литература [1, 4] 

|
|
|


|





|

|
|
|






|
ЛАБОРАТОРНАЯ РАБОТА №1.3.
Тема: Резонанс в разветвлённой цепи переменного тока.
Цель: Экспериментальное исследование разветвлённой цепи переменного тока с параллельным соединением индуктивного и ёмкостного элементов и практическое достижение в ней резонанса токов.
Основные сведения.
Резонанс в разветвлённой цепи переменного тока с параллельным соединением индуктивного и ёмкостного элементовназывают резонансом токов.
 Рассмотрим разветвлённую цепь переменного тока с двумя параллельными ветвями (рисунок 31), содержащими элементы с параметрами R1,L,R2,C и полными сопротивлениями
Рассмотрим разветвлённую цепь переменного тока с двумя параллельными ветвями (рисунок 31), содержащими элементы с параметрами R1,L,R2,C и полными сопротивлениями  ,
,  соответственно, где
соответственно, где  – реактивное сопротивление катушки индуктивности,
– реактивное сопротивление катушки индуктивности,  – реактивное сопротивление конденсатора, а f – частота питающего напряжения. В рассматриваемой цепи напряжения на первой и второй ветвях одинаковы и равны напряжению
– реактивное сопротивление конденсатора, а f – частота питающего напряжения. В рассматриваемой цепи напряжения на первой и второй ветвях одинаковы и равны напряжению 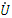 на входных зажимах. Согласно первому закону Кирхгофа ток
на входных зажимах. Согласно первому закону Кирхгофа ток 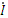 в неразветвлённой части цепи равен
в неразветвлённой части цепи равен  , где
, где  – ток в первой ветви,
– ток в первой ветви,  – ток во второй ветви,
– ток во второй ветви,  – полнаяпроводимость первой ветви,
– полнаяпроводимость первой ветви,  – активнаяпроводимость первой ветви,
– активнаяпроводимость первой ветви,  – реактивнаяпроводимость первой ветви,
– реактивнаяпроводимость первой ветви, 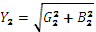 – полнаяпроводимость второй ветви,
– полнаяпроводимость второй ветви,  – активнаяпроводимость второй ветви,
– активнаяпроводимость второй ветви,  – реактивнаяпроводимость второй ветви. Токи в цепи имеют по две составляющих – активную и реактивную. Ток, текущий в первой ветви,
– реактивнаяпроводимость второй ветви. Токи в цепи имеют по две составляющих – активную и реактивную. Ток, текущий в первой ветви,  , где
, где  – активная составляющая тока, совпадающая по фазе с напряжением,
– активная составляющая тока, совпадающая по фазе с напряжением,  – реактивная (индуктивная) составляющая, отстающая от напряжения на четверть периода (т.е. на угол
– реактивная (индуктивная) составляющая, отстающая от напряжения на четверть периода (т.е. на угол  ). Ток, протекающий во второй ветви,
). Ток, протекающий во второй ветви,  , где
, где  – активная составляющая тока, совпадающая по фазе с напряжением,
– активная составляющая тока, совпадающая по фазе с напряжением,  – реактивная (ёмкостная) составляющая, опережающая напряжение на четверть периода. Качественная векторная диаграмма рассматриваемой цепи показана на рисунке 32. Из диаграммы видно, что ток
– реактивная (ёмкостная) составляющая, опережающая напряжение на четверть периода. Качественная векторная диаграмма рассматриваемой цепи показана на рисунке 32. Из диаграммы видно, что ток  в неразветвлённой части цепи опережает напряжение на угол
в неразветвлённой части цепи опережает напряжение на угол  , что свидетельствует о преобладании ёмкостной нагрузки, т.е.
, что свидетельствует о преобладании ёмкостной нагрузки, т.е. 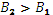 . Очевидно, что при
. Очевидно, что при  , ток
, ток  будет отставать от напряжения на угол
будет отставать от напряжения на угол  . При равенстве индуктивной и ёмкостной проводимостей ветвей (
. При равенстве индуктивной и ёмкостной проводимостей ветвей (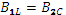 ) ток и напряжение на входе цепи будут совпадать по фазе (
) ток и напряжение на входе цепи будут совпадать по фазе ( ), что соответствует резонансному состоянию цепи. Таким образом, равенство индуктивной и ёмкостной проводимостей ветвей
), что соответствует резонансному состоянию цепи. Таким образом, равенство индуктивной и ёмкостной проводимостей ветвей 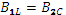 – является условием возникновения резонанса токов.
– является условием возникновения резонанса токов.
 Из условия резонанса токов следует, что добиться его можно изменением параметров элементов (R1,L,R2,C) или изменением частоты f питающего напряжения.
Из условия резонанса токов следует, что добиться его можно изменением параметров элементов (R1,L,R2,C) или изменением частоты f питающего напряжения.
Режиму резонанса токов характерны следующие признаки:
· Так как,, общее сопротивление цепи активное, то полная проводимость рассматриваемой цепи имеет минимальное значение, а сопротивление – максимальное.
· Ток в неразветвлённой части цепи становится минимальным.
· Поскольку, реактивные составляющие токов ветвей равны и противоположны, т.е. 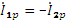 , то реактивная составляющая тока на входе цепи
, то реактивная составляющая тока на входе цепи  .
.
· Так как,  и
и  , то очевидно равны реактивные мощности
, то очевидно равны реактивные мощности  . Это означает, что в нашем случае, как и при резонансе напряжений, между катушкой индуктивности и конденсатором происходит обмен энергией, в котором источник питания не участвует. Энергия источника расходуется на восполнение потерь в активных сопротивлениях цепи.
. Это означает, что в нашем случае, как и при резонансе напряжений, между катушкой индуктивности и конденсатором происходит обмен энергией, в котором источник питания не участвует. Энергия источника расходуется на восполнение потерь в активных сопротивлениях цепи.
Таким образом, можно отметить, что резонанс токов в отличие от резонанса напряжений – явление безопасное для электроэнергетических установок. Большие токи в ветвях при резонансе токов возникают лишь в случае больших реактивных проводимостей (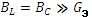 ) ветвей, т.е. при больших ёмкостях конденсаторов и малых индуктивностях катушек. С точки зрения передачи электроэнергии режим близкий к резонансу токов является благоприятным, так как при нём снижаются тепловые потери, повышаются коэффициент мощности и к.п.д. электроустановок.
) ветвей, т.е. при больших ёмкостях конденсаторов и малых индуктивностях катушек. С точки зрения передачи электроэнергии режим близкий к резонансу токов является благоприятным, так как при нём снижаются тепловые потери, повышаются коэффициент мощности и к.п.д. электроустановок.

Последовательность выполнения работы.
1. Собрать на лабораторном стенде схему исследуемой цепи (рисунок 33).
2. Включить в цепь минимальную ёмкость (С = 1 мкФ) батареи конденсаторов, замкнув на стенде контакт К4.
3. Подать на вход цепи с помощью лабораторного автотрансформатора (ЛАТР а) напряжение U = 150 В.
4. Поддерживая неизменным входное напряжение, увеличивать ёмкость батареи конденсаторов на 1 мкФ до максимального значения (34 мкФ). При этом измеренные в каждом случае значения напряжения, тока и коэффициента мощности, занести в таблицу 4.
Таблица 4.
| Номер ступени батареи конденсаторов | Ёмкость батареи конденсаторов, мкФ | U, В | I, A | IRL, A | IC, A | cos φ |
5. По данным таблицы 3 построить графики зависимостей
I = f(C), cos φ = f(C).
6. Построить по данным эксперимента в масштабах векторные диаграммы для трёх состояний цепи – до резонанса, близкого к резонансу и после резонанса.
 Примечание. Построение векторной диаграммы для разветвлённой цепи удобнее начинать с вектора напряжения
Примечание. Построение векторной диаграммы для разветвлённой цепи удобнее начинать с вектора напряжения 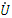 , которое одинаково на всех участках. Затем из начала вектора
, которое одинаково на всех участках. Затем из начала вектора 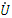 под углом 90° против хода часовой стрелки откладывают вектор
под углом 90° против хода часовой стрелки откладывают вектор  (ток в ёмкости опережает напряжение на четверть периода:
(ток в ёмкости опережает напряжение на четверть периода:  ). Ток
). Ток  в катушке индуктивности отстаёт от напряжения на угол
в катушке индуктивности отстаёт от напряжения на угол  . Но так как величина этого угла в нашем случае не известна, то исходя из того, что согласно первому закону Кирхгофа
. Но так как величина этого угла в нашем случае не известна, то исходя из того, что согласно первому закону Кирхгофа  (т.е. векторы
(т.е. векторы  ,
,  и
и 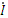 образуют треугольник токов), положение векторов
образуют треугольник токов), положение векторов  и
и 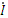 определяют методом засечек (рисунок 34).
определяют методом засечек (рисунок 34).
Очевидно, что до резонанса  , следовательно,
, следовательно,  и
и  , т.е. напряжение
, т.е. напряжение 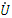 на входе цепи опережает ток
на входе цепи опережает ток 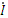 . В резонансе
. В резонансе  ,
, 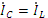 и
и  , т.е. напряжение
, т.е. напряжение 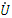 и ток
и ток 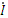 на входе цепи синфазны. После резонанса
на входе цепи синфазны. После резонанса  ,
,  , а
, а  и напряжение
и напряжение 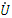 отстаёт от тока
отстаёт от тока 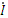 .
.
Содержание отчёта.
1. Схема исследуемой электрической цепи (рисунок 33).
2. Таблица измеренных величин (таблица 4).
3. Графики зависимостей I = f(C), cos φ = f(C).
4. Векторные диаграммы для трёх состояний цепи – до резонанса, близкого к резонансу и после резонанса.
Контрольные вопросы.
1. В каких цепях можно наблюдать резонанс токов и каково условие его возникновения?
2. Как практически можно добиться резонанса токов?
3. Назовите основные признаки резонанса токов.
4. Поясните, почему при резонансе токов ток в неразветвлённой части цепи принимает минимальное значение?
5. Какой характер нагрузки соответствует случаям:  ,
,  ,
, 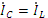 .
.
6. Каким образом практически можно увеличить коэффициент мощности электроустановки?
Литература [1, 4]
 | |||||
 | |||||
 |
ЛАБОРАТОРНАЯ РАБОТА №1.4.
Тема: Трёхфазные цепи с соединением электропотребителей по схеме “звезда”.
Цель: Экспериментальное исследование трёхфазной цепи переменного тока с электроприёмниками соединёнными по схеме “звезда”.
Основные сведения.
В технике, кроме однофазных электрических цепей, широкое применение находят многофазные цепи. Под симметричной многофазной электрической цепью понимают совокупность электрических цепей, в которых действуют несколько э.д.с. с одинаковыми частотами и амплитудами, сдвинутыми по фазе относительно друг друга на определенные равные углы.
Практическое применение нашли симметричные двенадцати- и шестифазные системы – в выпрямителях (угол сдвига фаз между э.д.с. у них составляет соответственно 30° и 60°), двухфазные – в автоматике (угол сдвига фаз между э.д.с. 90°). Однако преимущественное распространение получила трёхфазная система (угол сдвига фаз между э.д.с. 120°), которая повсеместно применяется в промышленности, сельском хозяйстве, при производстве и передаче электрической энергии.
Трёхфазная цепь состоит из трёх основных элементов: трёхфазного генератора, в котором механическая энергия преобразуется в электрическую с трёхфазной системой э.д.с.; линии передачи со всем необходимым оборудованием; приёмников (потребителей), которые могут быть как трёхфазными (например, трёхфазные асинхронные двигатели), так и однофазными (например, лампы накаливания). В период зарождения трёхфазных систем имелись попытки использовать несвязанную систему, в которой фазы обмотки генератора не были электрически соединены между собой, и каждая фаза соединялась со своим приёмником двумя проводами. Такие системы не получили применения вследствие их неэкономичности: для соединения генератора с приёмником требовалось шесть проводов. Более совершенными и экономичными являются связанные цепи, в которых фазы обмотки электрически соединены между собой. Наиболее распространёнными являются соединения "звезда" и "треугольник".
Трёхфазные связанные цепи в зависимости от способа соединения фаз трёхфазных источников питания и трёхфазных потребителей электроэнергии могут быть трёхпроводными или четырёхпроводными.
Трёхпроводная трёхфазная цепь получается при соединении источника с приёмником тремя проводами, при этом способы соединения фаз источников и фаз потребителей в них могут быть различными.
Рассмотрим трёхпроводную цепь при соединении “звездой” как фазных обмоток источника, так и фаз приёмников (рисунок 35).
В такой цепи концы фаз источника соединяют в одну общую точку N, называемую нейтральной точкой. Аналогично концы фаз приёмников также соединяют в одну точку n.
 |
Провода A − a, B − b и C − c, соединяющие начала фаз источника и приёмника, называются линейными.
Обычно фазные э.д.с. трёхфазного источника имеют одинаковые амплитуды (EmA = EmB = EmC = Em) и сдвинуты по фазе относительно друг друга на один и тот же угол 120°. Если э.д.с. одной фазы (например, фазы A) принять за исходную и считать её начальную фазу равной нулю, то выражения комплексных значений фазных э.д.с. можно записать в виде:



Такая система э.д.с. называется симметричной.
Полные фазные сопротивления приёмников:
 a =
a =  ;
;  b =
b = 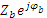 ;
;  c =
c = 
Приёмники, имеющие равные по модулю (Za = Zb = Zc = Zф) и по характеру (φa = φb = φc = φф) сопротивления, создают так называемую симметричную нагрузку.
В трёхфазных цепях различают фазные и линейные напряжения. Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (UA, UB, UC - у источника; Ua, Ub, Uc - у приёмника). Если пренебречь потерями энергии в фазных обмотках источника, то можно считать, что фазные напряжения источника (согласно второму закону Кирхгофа) равны соответствующим фазным э.д.с., т.е. 
Линейное напряжение (UЛ) – напряжение между линейными проводами (UAB, UBC, UCA) или между одноимёнными выводами разных фаз источника (нагрузки).
В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений (рис.35) уравнения по второму закону Кирхгофа, связывающие линейные и фазные напряжения источника имеют вид:  AB =
AB =  A −
A −  B ;
B ;  BC =
BC =  B −
B −  C ;
C ;  CA =
CA =  C −
C −  A . Аналогично для нагрузки –
A . Аналогично для нагрузки –  AB =
AB =  a −
a −  b ;
b ;  BC =
BC =  b −
b −  c ;
c ;  CA =
CA =  c −
c −  a .
a .
 Согласно этим выражениям построена топографическая диаграмма (рисунок 36), из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична, т.е.
Согласно этим выражениям построена топографическая диаграмма (рисунок 36), из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична, т.е.  AB ,
AB ,  BC ,
BC ,  CA равны по величине и сдвинуты по фазе относительно друг друга на 120°, и опережают соответственно векторы фазных напряжений (
CA равны по величине и сдвинуты по фазе относительно друг друга на 120°, и опережают соответственно векторы фазных напряжений ( A ,
A ,  B ,
B ,  C ) на угол 30°. Действующие значения линейных напряжений можно определить графически по векторной диаграмме или по формуле: UЛ=2UФ cos 30°=
C ) на угол 30°. Действующие значения линейных напряжений можно определить графически по векторной диаграмме или по формуле: UЛ=2UФ cos 30°=  UФ, которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений (например –
UФ, которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений (например –  A ,
A ,  B и
B и  АВ ).
АВ ).
По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи:
· Фазные (IФ) – это токи в фазах генератора и приёмников.
· Линейные (IЛ) – токи в линейных проводах.
Из схемы на рисунке 35 видно, что при соединении “звездой” фазные и линейные токи равны IФ = IЛ.
Фазные (они же линейные) токи рассчитываются по закону Ома:
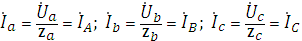 ,
,
и при этом согласно первому закону Кирхгофа  .
.
При симметричной нагрузке, если пренебречь сопротивлением проводов, действующие значения фазных напряжений приёмника и источника, можно считать одинаковыми и равными по модулю (UA = Ua, UB = Ub, UC = Uc). Очевидно, при этом будут равны и модули токов, поэтому для определения токов достаточно выполнить расчёт в одной фазе.
При несимметричной нагрузке между нейтральными точками n приёмникаи N источникаэлектроэнергии возникает напряжение смещения нейтрали UnN, приводящее к перекосу фазных напряжений на приёмниках, как это видно на топографической диаграмме (рисунок 37).
 Анализируя диаграмму (рисунок 37), не сложно увидеть, что изменение (уменьшение) тока
Анализируя диаграмму (рисунок 37), не сложно увидеть, что изменение (уменьшение) тока  , вызванное изменением (увеличением) сопротивления фазы а нагрузки, вызвало такое изменение токов двух других фаз, при котором алгебраическая сумма токов остаётся равной нулю. Причём, если сопротивления фаз b и c остаются неизменными, то изменение токов в них вызовет изменение (уменьшение) приложенных к ним напряжений
, вызванное изменением (увеличением) сопротивления фазы а нагрузки, вызвало такое изменение токов двух других фаз, при котором алгебраическая сумма токов остаётся равной нулю. Причём, если сопротивления фаз b и c остаются неизменными, то изменение токов в них вызовет изменение (уменьшение) приложенных к ним напряжений  a ,
a ,  b ,
b ,  c . На диаграмме (рисунок 37) точка n сместилась относительно точки N, а “звезда” фазных напряжений (
c . На диаграмме (рисунок 37) точка n сместилась относительно точки N, а “звезда” фазных напряжений ( a ,
a ,  b ,
b ,  c ) нагрузки оказалась перекошенной и смещенной относительно “звезды” фазных напряжений (
c ) нагрузки оказалась перекошенной и смещенной относительно “звезды” фазных напряжений ( A ,
A ,  B ,
B ,  C ) источника. То есть перераспределение фазных напряжений нагрузки при неизменных напряжениях источника привело к появлению напряжения UnN между нулевыми точками приёмников и источника.
C ) источника. То есть перераспределение фазных напряжений нагрузки при неизменных напряжениях источника привело к появлению напряжения UnN между нулевыми точками приёмников и источника.
Поскольку схема (рисунок 35) представляет собой цепь с двумя узлами, то напряжение смещения нейтрали можно определить по формуле межузлового напряжения:

где:  a =
a =  / Z a;
/ Z a;  b = 1/ Z b;
b = 1/ Z b;  c = 1/ Z c – комплексы полных проводимостей фаз нагрузки.
c = 1/ Z c – комплексы полных проводимостей фаз нагрузки.
Очевидно, что теперь напряжения на фазах приёмника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что
 a =
a =  A -
A -  nN ;
nN ;  =
=  B -
B -  nN ;
nN ;  c =
c =  C -
C -  nN .
nN .
В режиме несимметричной нагрузки приходится рассчитывать токи в каждой из фаз, при этом согласно первому закону Кирхгофа:
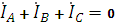
Таким образом, нарушение симметрии нагрузки в трёхпроводной цепи приводит к нарушению симметрии напряжений на приёмниках. Одни приёмники оказываются под пониженным напряжением и не развивают номинальной мощности, другие – под повышенным напряжением, что может вызвать их повреждение. Поэтому трёхпроводные цепи используют относительно редко и только при симметричной трёхфазной нагрузке (например, трёхфазные электродвигатели, электропечи, трансформаторы и др.).
 |
Четырёхпроводная трёхфазная цепь получается при соединении “звездой” как фазных обмоток источника, так и фаз приёмников, при этом нейтральные точки источника N и приёмника n соединяют проводом N – n называемым нейтральным (рисунок 38), уравнивающим потенциалы точек N и n.
 В этом случае напряжение смещения нейтрали UnN = 0 и перекоса фазных напряжений на нагрузке не наблюдается, т.е. UA = Ua, UB = Ub, UC = Uc.
В этом случае напряжение смещения нейтрали UnN = 0 и перекоса фазных напряжений на нагрузке не наблюдается, т.е. UA = Ua, UB = Ub, UC = Uc.
При этом токи рассчитываются, как и ранее по закону Ома.
Топографическая диаграмма токов и напряжений для такой цепи с несимметричной нагрузкой ( a ≠
a ≠  b ≠
b ≠  c ) представлена на рисунке 39.
c ) представлена на рисунке 39.
Векторы токов на диаграмме строят относительно векторов соответствующих фазных напряжений. Углы сдвига фаз между токами и напряжениями на приёмниках определяются по формуле:  . Из диаграммы видно, что вектор тока
. Из диаграммы видно, что вектор тока  сонаправлен с вектором напряжения
сонаправлен с вектором напряжения 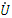 a , т.е. нагрузка фазы а имеет активный характер (
a , т.е. нагрузка фазы а имеет активный характер ( ). Вектор тока
). Вектор тока  опережает вектор напряжения
опережает вектор напряжения  , т.е. нагрузка фазы b активно-ёмкостного характера (
, т.е. нагрузка фазы b активно-ёмкостного характера ( ), а в фазе c, т.к. вектор тока
), а в фазе c, т.к. вектор тока  отстаёт от вектора напряжения
отстаёт от вектора напряжения  , – приёмник с активно-индуктивным сопротивлением (
, – приёмник с активно-индуктивным сопротивлением (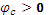 ):.
):.
Ток, протекающий в нейтральном проводе I0, определяетсяпо первому закону Кирхгофа для нейтральной точки источника или приёмника:  .
.
При симметричной нагрузке ( a =
a =  b =
b =  c ) фазные (они же линейные) токи будут равны по модулю и сдвинуты относительно фазных напряжений на один и тот же угол, т.е. векторы токов на диаграмме образуют симметричную трёхлучевую звезду. Очевидно, что в этом случае ток в нейтральном проводе отсутствует:
c ) фазные (они же линейные) токи будут равны по модулю и сдвинуты относительно фазных напряжений на один и тот же угол, т.е. векторы токов на диаграмме образуют симметричную трёхлучевую звезду. Очевидно, что в этом случае ток в нейтральном проводе отсутствует:  , поэтому необходимость в этом проводе отпадает. Однако во многих случаях (например, для осветительной нагрузки) нейтральный провод необходим, поскольку нет оснований рассчитывать на полную симметрию такого потребителя. В нейтральном проводе четырёхпроводной осветительной магистрали запрещена установка выключателей или защитных аппаратов (например, предохранителей). Поскольку при отключении нейтрального провода при не одинаковой загрузке (что часто бывает при отключении или выходе из строя одного из потребителей) возникнет перекос фазных напряжений на работающих приёмниках, который может привести к аварийной ситуации.
, поэтому необходимость в этом проводе отпадает. Однако во многих случаях (например, для осветительной нагрузки) нейтральный провод необходим, поскольку нет оснований рассчитывать на полную симметрию такого потребителя. В нейтральном проводе четырёхпроводной осветительной магистрали запрещена установка выключателей или защитных аппаратов (например, предохранителей). Поскольку при отключении нейтрального провода при не одинаковой загрузке (что часто бывает при отключении или выходе из строя одного из потребителей) возникнет перекос фазных напряжений на работающих приёмниках, который может привести к аварийной ситуации.



