Темы для изучения
Закон сохранения энергии. Закон сохранения энергии механических систем. Открытые и замкнутые системы. Маятник Обербека, энергия поступательного движения тела, энергия вращательного движения тела, потенциальная энергия, работа сил трения, момент инерции, угловая скорость, угловое ускорение, мгновенная скорость, момент инерции.
Принцип
Крестовина, которая может вращаться вокруг своей оси, движется с постоянным угловым ускорением под действием внешней силы. Определяется зависимость потенциальной энергии системы, энергии поступательного и вращательного движения компонентов системы, от времени.
Рисунок 1. Маятник Обербека. Экспериментальная установка. для изучения закона сохранения энергии.
Цель работы:
Проверить выполнение закона сохранения механической энергии. Оценить величину сил трения.
Приборы и оборудование: маятник Обербека, набор грузов, штангенциркуль, секундомер.
Обозначения
I – момент инерции, 
e – угловое ускорение, 
М – вращающий момент, 
h0 – высота падения груза, м (отсчитывается от положения минимума)
h1 – высота подъёма груза, м (отсчитывается от положения минимума)
t0 – время падения груза, с
t1 – время подъёма груза, с
m – масса падающего груза, кг
v – линейная скорость падающего груза, 
w – угловая скорость крестовины, 
а0 – линейное ускорение падающего груза, 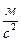
 – сила трения, возникающая при вращении крестовины, Н
– сила трения, возникающая при вращении крестовины, Н
Т – сила натяжения нити, Н
r – радиус шкива, м
R – расстояние от оси вращения до центра масс груза, закреплённого на крестовине
m2 – масса груза закреплённого на крестовине, кг
l – длина стержня крестовины, м
m3 – масса стержня крестовины, кг
Краткая теория
Закон сохранения энергии: энергия не возникает из ничего и не исчезает бесследно, а переходит из одного вида в другой.
 – потенциальная энергия колеса Максвелла, поднятого на высоту h0 от нулевого уровня (1)
– потенциальная энергия колеса Максвелла, поднятого на высоту h0 от нулевого уровня (1)
 – кинетическая энергия поступательного движения (2)
– кинетическая энергия поступательного движения (2)
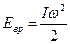 – кинетическая энергия вращательного движения (3)
– кинетическая энергия вращательного движения (3)
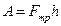 – работа сил трения на пути h (4)
– работа сил трения на пути h (4)
 – закон сохранения энергии на пути вниз (5)
– закон сохранения энергии на пути вниз (5)
 – закон сохранения энергии на пути вверх (6)
– закон сохранения энергии на пути вверх (6)
Вычитая из выражения (5) выражение (6) и преобразовав, получаем:
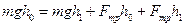 (7)
(7)
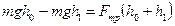 (8)
(8)
 (9)
(9)
Формула (9) является рабочей для расчёта силы трения.
Докажем, что движение груза вниз в маятнике Обербека является равноускоренным.
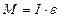 – основной закон динамики вращательного движения (10)
– основной закон динамики вращательного движения (10)
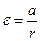 – взаимосвязь линейного и углового ускорения (11)
– взаимосвязь линейного и углового ускорения (11)
 – второй закон Ньютона для маятника Обербека (12)
– второй закон Ньютона для маятника Обербека (12)
 – линейное ускорение груза в маятнике Обербека (13)
– линейное ускорение груза в маятнике Обербека (13)
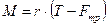 – вращающий момент маятника Обербека (14)
– вращающий момент маятника Обербека (14)
В основной закон динамики вращательного движения (выражение 10) подставляем вращающий момент (14) и угловое ускорение (11)
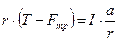 (15)
(15)
Из второго закона Ньютона (выражение 12) находим натяжение нити
 (16)
(16)
Подставляем натяжение нити (16) в выражение (15)
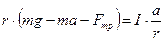 (17)
(17)
Преобразовав (17), получаем выражение (20) для линейного ускорения
 (18)
(18)
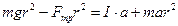 (19)
(19)
 (20)
(20)
Из выражения (20) можно сделать вывод, что в принятом нами приближении (постоянная сила трения) движение груза в маятнике Обербека является равноускоренным. Похожее выражение можно получить и для подъёма колеса. Это означает, что законы кинематики равноускоренного движения применимы к маятнику Обербека.
Тогда для движения груза вниз
 (21)
(21)
 (22)
(22)
 (23)
(23)
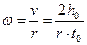 (24)
(24)
 (25)
(25)
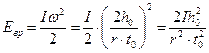 (26)
(26)
Сложив (25) и (26), получаем выражение (28) - закона сохранения энергии в нашем случае, в справедливости которого нужно убедиться в результате выполнения данной лабораторной работы
 (27)
(27)
 (28)
(28)
Формула (28) является рабочей.
Моменты инерции тел различной формы
Момент инерции крестовины рассчитывается по формуле
 (29)
(29)
где
 – момент инерции оси и дисков
– момент инерции оси и дисков
 момент инерции груза на стержне крестовины
момент инерции груза на стержне крестовины
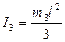 момент инерции стержня. Ось вращения перпендикулярна к стержню и проходит через его конец.
момент инерции стержня. Ось вращения перпендикулярна к стержню и проходит через его конец.
Ход работы
1. Измерьте диаметр малого шкива  с помощью штангенциркуля и рассчитайте его радиус.
с помощью штангенциркуля и рассчитайте его радиус.
2. Закрепите на концах стержней цилиндрические грузы так, чтобы маятник находился в состоянии безразличного равновесия.
3. Намотайте нить на шкив малого диаметра. Подвесьте груз и измерьте высоту падения h0. Результат занесите в таблицу.
4. Аккуратно, без толчка, отпустите крестовину, запустив при этом секундомер. Крестовина начнет раскручиваться и груз опустится, достигнет точки минимума и по инерции поднимется на какую-то высоту вверх. Зафиксируйте время t0 опускания груза до точки минимума, и время t1 последующегоподъёма вверх (до верхней точки), и саму высоту подъёма h1. Для этого рукой затормозите крестовину в верхней точке подъёма и одновременно остановите секундомер. Весь этот пункт выполните три раза, результаты занесите в таблицу.
5. Вращая крестовину, поднимите груз в верхнее положение на высоту, равную средней высоте свободного подъёма в предыдущем опыте. Повторите действия, обозначенные в пункте 4. Результаты занесите в таблицу.
6. Выполняйте пункт 5 до тех пор, пока высота подъема колеса не уменьшится примерно в два раза по сравнению с первым опытом
Обработка результатов
1. Для качественной оценки результатов эксперимента, постройте график зависимости высоты подъёма колеса от времени. Примерный вид графика, при безошибочно выполненном эксперименте, показан на рисунке 2. По горизонтальной оси отложено суммарное время движения груза.
2. Используя формулу (9) рассчитайте значения силы трения для каждого цикла. Найдите среднее значение и среднеквадратичную ошибку.
3. Вычислите значение правой части рабочей формулы (28) для всех значений h0, t0,.Это значение в среднем должно совпасть с величиной силы тяжести mg. Если это так, вы доказали справедливость закона сохранения механической энергии с использованием маятника Обербека.
4. Оформите отчет о выполненной лабораторной работе согласно требованиям.
Таблица 1.
| Номер п/п | Высота падения h0, м | Время падения t0, с | Высота подъёма h1, м | Время подъёма t1, с | Среднее значение | ||
| t0, с | h1,м | t1, с | |||||