УЧЕБНО – МЕТОДИЧЕСКОЕ ПОСОБИЕ
к выполнению курсового проекта по курсу
«Диагностика и надежность АС»
для студентов специализации
«Автоматизация производственных процессов»
Уфа 2003
РАСЧЕТ НАДЕЖНОСТИ ИНФОРМАЦИОННОЙ СИСТЕМЫ
Задание1/
По структурной схеме надежности информационной системы и заданным значениям интенсивности отказов ее элементов:
1) построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0,1 – 0,2;
2) определить время наработки системы соответствующее заданному γ (гамма-процентному ресурсу системы);
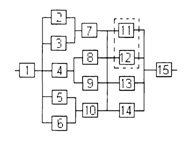
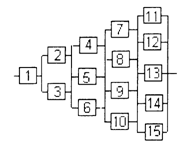
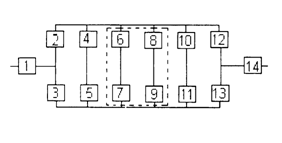
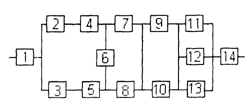
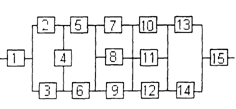
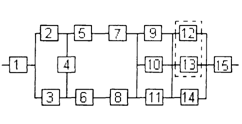
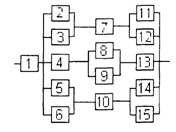
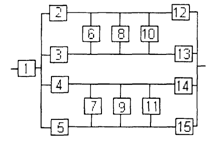
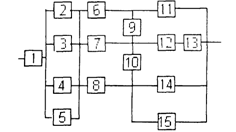
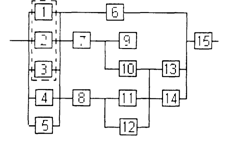
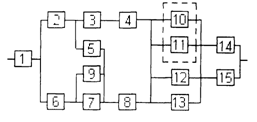
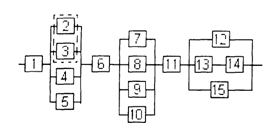
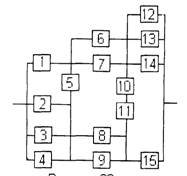
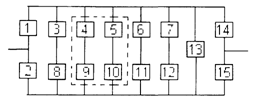
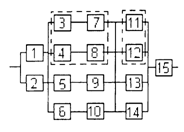
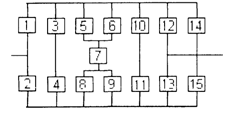
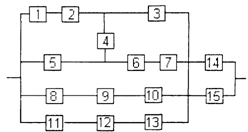
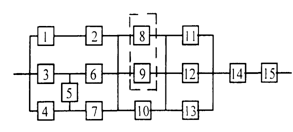
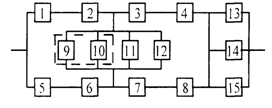
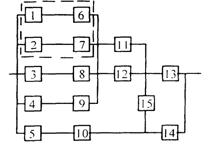
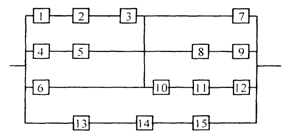
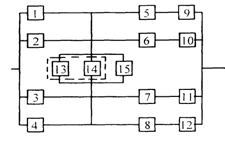
3) обеспечить при заданном γ (гамма-процентном ресурсе) увеличение времени наработки системы не менее чем в 1,5 раза за счет структурного резервирования элементов системы. Варианты структурных схем и значения интенсивностей отказов приведены на рис. 7 и в табл. 2, соответственно.
Пример расчета
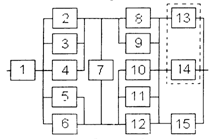
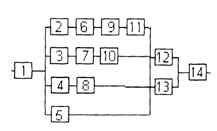
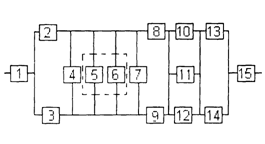
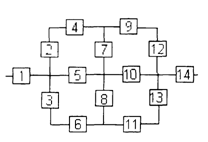
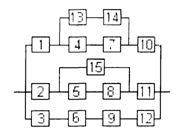
Структурная схема надежности приведена на рис. 1.
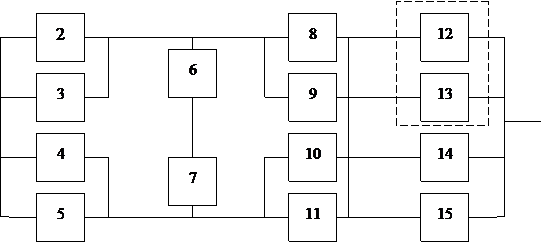 |
Рис. 1.
Рис. 1
Значения интенсивности отказов элементов составляют:
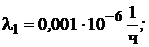
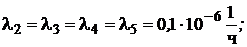
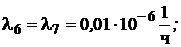
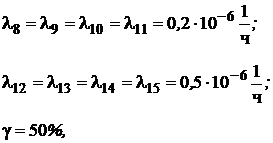
где γ – (гамма-процентный ресурс системы) – вероятность безотказной работы системы, выраженный в процентах, по истечении определенного времени непрерывной работы (наработки) системы.
Все элементы системы работают в режиме нормальной эксплуатации. Резервирование отдельных элементов или групп элементов должно осуществляться идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными. На схемах обведенные пунктиром m элементов являются функционально необходимыми.
Расчет
1. В исходной схеме элементы 2 и 3 образуют параллельное соединение. Заменяем их квазиэлементом А. Учитывая, что p2 = p3, получим:
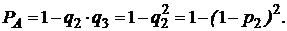 (1)
(1)
2. Элементы 4 и 5 также образуют параллельное соединение, заменив которое элементом В и учитывая, что p4 = p5, получим:
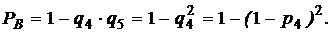 (2)
(2)
3. Элементы 6 и 7 в исходной схеме соединены последовательно. Заменяем их элементом С, для которого при p6 = p7:
 (3)
(3)
4. Элементы 8 и 9 образуют параллельное соединение. Заменяем их элементом D, для которого при p 8 = p 9, получим:
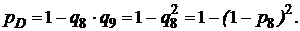 (4)
(4)
5. Элементы 10 и 11 образуют параллельное соединение. Заменяем их элементом Е, причем, так как p 10 = p 11 = p 8, то
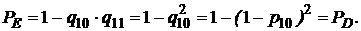 (5)
(5)
6. Элементы 12, 13, 14 и 15 образуют соединение «2 из 4», которое заменяем элементом F. Так как p 12 = p 13 = p 14 = p 15, то для определения вероятности безотказной работы элемента F можно воспользоваться выражением, в основе которого лежит формула биноминального распределения (биноминальному распределению подчиняется дискретная случайная величина k – число появлений некоторого события в серии из n опытов, если в отдельном опыте вероятность появления события составляет p).
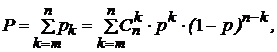
где  – биноминальный коэффициент, называемый «числом сочетаний по k из n » (т. е. сколькими разными способами можно реализовать ситуацию k из n).
– биноминальный коэффициент, называемый «числом сочетаний по k из n » (т. е. сколькими разными способами можно реализовать ситуацию k из n).
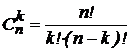 .
.
Поскольку для отказа системы «m из n » достаточно, чтобы количество исправных элементов было меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0, 1, …, (m – 1):

Аналогичным образом можно найти вероятность безотказной работы как сумму для k = m, m + 1, …, n:
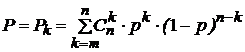 .
.
В данном конкретном случае, при n = 4 и m = 2, вероятность безотказной работы элемента F определится выражением:
|

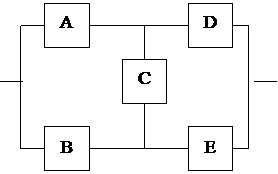
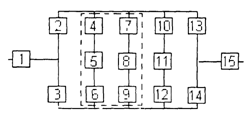
7. Преобразованная схема изображена на рис. 2.
 | |||
 | |||
Рис. 2
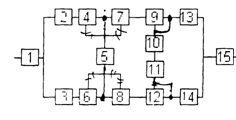
8. Элементы А, В, С, D и Е (рис. 2) образуют мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом минимальных путей. Логическая схема мостиковой системы по методу минимальных путей приведена на рис. 3
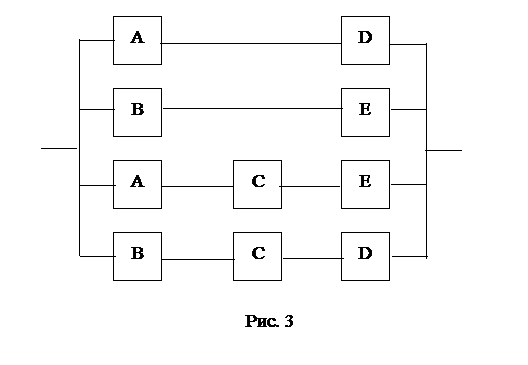 |
Система, изображенная на рис. 3 работоспособна до тех пор, пока работоспособны элементы А и D или – B и E, или – A, C и E, или – B, C и D. Таким образом, вероятность работы квазиэлемента G можно определить по формуле:
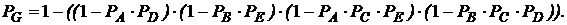 (7)
(7)
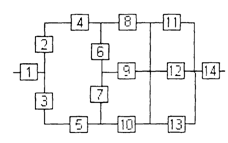
9. После преобразования схема примет вид, изображенный на рис. 4.
 |
Рис. 4
10. В преобразованной схеме (рис. 4) элементы 1, G, и F образуют последовательное соединение. Тогда вероятность безотказной работы всей системы определяется выражением:
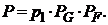 (8)
(8)
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 1) подчиняются экспоненциальному закону:
 (9)
(9)
12. Результаты расчетов вероятностей безотказной работы элементов 1 – 15 исходной схемы по формуле (9) для наработки до 3·106 часов представлены в табл. 1.
Таблица 1
| Наработка, t – 1 000 000 ч | |||||||||
| Элемент | 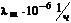
| 0,5 | 1,5 | 2,5 | 1,9 | 2,85 | |||
| 0,001 | 0,9990 | 0,9985 | 0,9985 | 0,9980 | 0,9975 | 0,9970 | 0,9981 | 0,9972 | |
| 2 – 5 | 0,1 | 0,9512 | 0,9048 | 0,8607 | 0,8187 | 0,7788 | 0,7408 | 0,8270 | 0,7520 |
| 6,7 | 0,01 | 0,9950 | 0,9900 | 0,9851 | 0,9802 | 0,9753 | 0,9704 | 0,9812 | 0,9719 |
| 8 – 11 | 0,2 | 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | 0,6839 | 0,5655 |
| 12 – 15 | 0,5 | 0,7788 | 0,6065 | 0,4724 | 0,3679 | 0,2865 | 0,2231 | 0,3867 | 0,2405 |
| A, B | - | 0,9976 | 0,9909 | 0,9806 | 0,9671 | 0,9511 | 0,9328 | 0,9701 | 0,9385 |
| C | - | 0,9900 | 0,9802 | 0,9704 | 0,9608 | 0,9512 | 0,9418 | 0,9627 | 0,9446 |
| D, E | - | 0,9909 | 0,9671 | 0,9328 | 0,8913 | 0,8452 | 0,7964 | 0,9001 | 0,8112 |
| F | - | 0,9639 | 0,8282 | 0,6449 | 0,4687 | 0,3246 | 0,2173 | 0,5018 | 0,2458 |
| G | - | 1,0000 | 1,0000 | 0,9999 | 0,9994 | 0,9979 | 0,9940 | 0,9996 | 0,9955 |
| P | - | 0,9629 | 0,8270 | 0,6439 | 0,4675 | 0,3231 | 0,2153 | 0,5006 | 0,2440 |
| F' | - | 0,9993 | 0,9828 | 0,9173 | 0,7954 | 0,6413 | 0,4859 | 0,8234 | 0,5311 |
| P' | - | 0,9983 | 0,9813 | 0,9158 | 0,7934 | 0,6383 | 0,4815 | 0,8215 | 0,5272 |
13. Результаты расчетов вероятностей безотказной работы квазиэлементов А, В, С, D, Е, F и G по формулам (1) – (7) и также представлены в табл. 1.
14. На рис. 5 представлен график зависимости вероятности безотказной работы системы Р от времени (наработки) t.

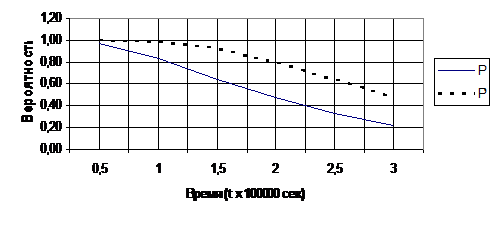
Рис. 5
15. По графику (рис. 5, кривая Р) находим для γ = 50% (Р = 0.5) γ-процентную наработку системы t = 1,9·106 ч.
16. Проверочный расчет при t = 1,9·106 ч показывает (табл. 1), что
P γ = 0,5006 ~ 0,5.
17. По условиям задания находим время, превышающее в 1,5 раза время, соответствующее вероятности безотказной работы, равное 0,5 (P γ = 0,5):
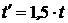 . (10)
. (10)
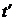 = 1,5·1,9·106 = 2,85·106 ч.
= 1,5·1,9·106 = 2,85·106 ч.
18. Расчет показывает (табл. 1), что при 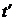 = 2,85·106 ч для элементов преобразованной схемы (рис. 4) p1 (
= 2,85·106 ч для элементов преобразованной схемы (рис. 4) p1 ( 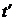 ) = 0,9972, pG (
) = 0,9972, pG ( 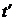 ) = 0,9955 и pF (
) = 0,9955 и pF ( 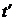 ) = 0,2458. Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F (система «2 из 4»
) = 0,2458. Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F (система «2 из 4»
в исходной схеме (рис. 1)), и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.
19. Для того чтобы при 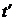 = 2.85 × 106 ч система в целом имела вероятность безотказной работы P’ = 0,5, надо найти необходимую вероятность безотказной работы элемента F. Так как
= 2.85 × 106 ч система в целом имела вероятность безотказной работы P’ = 0,5, надо найти необходимую вероятность безотказной работы элемента F. Так как

где 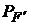 – необходимая вероятность безотказной работы элемента F, то
– необходимая вероятность безотказной работы элемента F, то
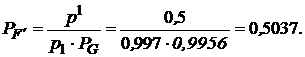 (11)
(11)
20. Для элемента F системы «2 из 4» резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов достаточно сложно, так как число элементов должно быть целым и функция 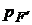 = f(n) дискретна.
= f(n) дискретна.
21. Для повышения надежности системы «2 из 4» добавляем к ней элементы, идентичные по надежности исходным элементам 12 – 15, до тех пор, пока вероятность безотказной работы квазиэлемента F не достигнет заданного значения:
- добавляем элемент 16, получаем систему «2 из 5»:
|
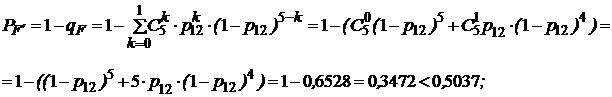
- добавляем элемент 17, получаем систему «2 из 6»:
|
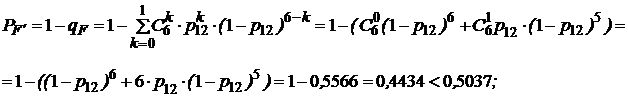
- добавляем элемент 18, получаем систему «2 из 7»:
|
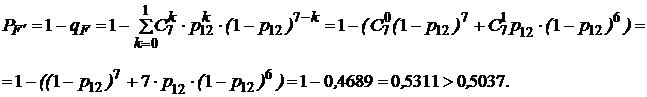
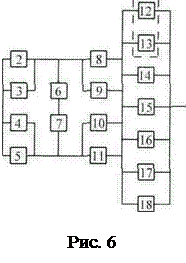 22. Таким образом, для повышения надежности до требуемого уровня, необходимо в исходной схеме (рис. 1) систему «2 из 4» достроить элементами 16, 17 и 18 до системы «2 из 7» (рис. 6).
22. Таким образом, для повышения надежности до требуемого уровня, необходимо в исходной схеме (рис. 1) систему «2 из 4» достроить элементами 16, 17 и 18 до системы «2 из 7» (рис. 6).
23. Результаты расчетов вероятностей безотказной работы квазиэлемента «F» («2 из 7») и системы в целом Р’ представлены в табл. 1.
24. Расчеты показывают, что при t’ = 2,85×106 ч, Р’ = 0,5272 > 0,5, что соответствует условию задания.
ВЫВОД
1. По данным расчета вероятности безотказной работы системы от времени построен график P(t).
2. По графику найдено время, соответствующее 50% g-процентному ресурсу системы (t = 1,9 × 106 ч).
3. Для увеличения наработки системы в 1,5 раза при 50% g -процентном ресурсе системы предложено нагруженное резервирование основных элементов 12, 13, 14 и 15 идентичными по надежности резервными элементами 16, 17 и 18.
4. Рассчитана вероятность безотказной работы системы с повышенной надежностью от времени, построен график P’(t) системы с повышенной надежностью, на графике (рис. 7) показано время (t’ = 2,85 × 106 ч) соответствующее 50% g -процентному ресурсу.

|

|
|

|


|
|
|
|
|
|
|
|

|
|

|
|
|


|
|

|
Таблица 2
Численные значения параметров к заданию
| № вар. | γ% | 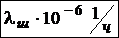 Интенсивности отказов элементов, х10-6 1/ч Интенсивности отказов элементов, х10-6 1/ч
| ||||||||||||||
| 0.1 | 1.0 | 0.5 | 1.0 | 0.1 | ||||||||||||
| 0.2 | 0.5 | 1.0 | 0.1 | |||||||||||||
| 0.1 | 1.0 | 2.0 | 1.0 | 5.0 | 0.2 | |||||||||||
| 0.05 | 1.0 | 0.5 | 0.2 | 0.02 | ||||||||||||
| 0.01 | 0.05 | 0.1 | 0.5 | 1.0 | ||||||||||||
| 0.01 | 0.05 | 1.0 | 0.05 | 0.1 | - | |||||||||||
| 0.05 | 0.5 | 0.05 | 0.005 | 0.1 | 0.2 | 0.1 | - | |||||||||
| 0.1 | 0.5 0.2 | 0.01 | 0.5 | 0.1 | - | |||||||||||
| 0.03 | 0.5 0.2 | 1.0 | 0.03 | 0.1 | - | |||||||||||
| 0.1 | 0.5 | 1.0 | 0.5 | 1.0 | 0.1 | - | ||||||||||
| 0.05 | 0.2 | 0.5 | 0.2 | 0.1 | ||||||||||||
| 0.02 | 0.1 | 1.0 | 2.0 | 0.1 | 0.05 | |||||||||||
| 0.01 | 0.2 | 0.1 | 1.0 | 0.5 | 0.1 | - | ||||||||||
| 0.01 | 0.1 | 10.0 | 0.2 | 10.0 | 0.5 | 0,3 | ||||||||||
| 0.01 | 1.0 | 5.0 | 0.2 | 5.0 | 0.1 | - | ||||||||||
| 0.1 | 1.0 | 2.0 | 1.0 | 5.0 | 3.0 | 1.0 | 0.05 | |||||||||
| 0.1 | 5.0 | 1.0 | 5.0 | 10.0 | 5.0 | 1.0 | 0.2 | |||||||||
| 0.01 | 1.0 | 0.1 | - | |||||||||||||
| 0.1 | 5.0 | 0.5 | 5.0 | 1.0 | 3.0 | 1.0 | 5.0 | 0.5 | 5.0 | |||||||
| 0.1 | 10.0 | 20.0 | 10.0 | |||||||||||||
| 0.1 | 1.0 | 0.5 | 2.0 | 0.5 | 0.2 | 1.0 | ||||||||||
| 1.0 | 0.2 | 0.5 | 1.0 | 0.5 | 1.0 | 1.0 | 0.1 |
Продолжение табл. 2
| 0.5 | 0.2 | 1.0 | 0.5 | 1.0 | 0.5 | 1.0 | 0.2 | 0.5 | 1.0 | 0.2 | ||||||
| 1.0 | 2.0 | 4.0 | 2.0 | 4.0 | 5.0 | 1.0 | ||||||||||
| 0.5 | 10.0 | 0.5 | 5.0 | 0.8 | 5.0 | 1.0 | 5.0 | |||||||||
| 1.0 | 2.0 | 3.0 | 5.0 | 2.0 | 5.0 | 1.0 | ||||||||||
| 5.0 | 10.0 | 15.0 | 10.0 | 10.0 | 15.0 | 10.0 | ||||||||||
| 1.0 | 2.0 | 5.0 | 2.0 | 1.0 | ||||||||||||
| 5.0 | 50.0 | 30.0 | 1.0 | |||||||||||||
| 2.0 | 1.0 | 2.0 | 1.0 | 5.0 | 2.0 | 5.0 | 2.0 | 1.0 | 2.0 | 1.0 | 2.0 | 1.0 | ||||
| 2.0 | 1.0 | 2.0 | 1.0 | 5.0 | 2.0 | 5.0 | 2.0 | 1.0 | 2.0 | 1.0 | 2.0 | 1.0 | ||||
| 5.0 | 2.0 | 5.0 | 1.0 | 2.0 | 3.0 | 1.0 | ||||||||||
| 1.0 | 2.0 | 3.0 | 4.0 | 2.0 | 3.0 | 5.5 | 0.2 | 0.5 | ||||||||
| 6.0 | 3.0 | 6.0 | 3.0 | 6.0 | 20.0 | 10.0 | ||||||||||
| 1.0 | 2.0 | 1.0 | 2.0 | 1.0 | 5.0 | |||||||||||
| 2.0 | 1.0 | 0.6 | ||||||||||||||
| 10.0 | 30.0 | 5.0 | 2.0 | |||||||||||||
| 3.0 | 2.0 | 1.0 | 2.0 | 3.0 | 2.0 | |||||||||||
| 8.0 | 3.0 | 5.0 | 2.0 | |||||||||||||
| 2.0 | 5.0 | 8.0 | 2.0 | 5.0 | 8.0 | |||||||||||
| № вар. | ||||||||||||||||
Задание 2
Расчет показателей надежности систем автоматизации (СА) с восстановлением (метод Колмогорова).
2.1. Исходные данные выбираются из таблицы 3.
2.2. Структурная схема состояний системы.
2.3.Система уравнений Колмогорова и ее решение для установившегося режима.
2.4. Определение коэффициентов готовности и простоя системы. Интенсивность отказа основного и резервных элементов принят равным 0,1, а интенсивность восстановления 0,5
Курсовой проект должен содержат следующие данные.
3.1. Титульный лист.
3.2. Содержание.
3.3 Изложение всех пунктов задания.
3.4. Выводы в конце каждого раздела.
3.5. Список использованных источников.
Полезные рекомендации
При выполнении задания 2 можно воспользоваться книгой под редакцией Дружинина Г.В. Теория надежности радиоэлектронных систем. – М.: Энергия, 1976., где приведено множество примеров.
| Номер варианта | Число резервных элементов | Число ремонтных бригад |
(0-пассив. 1-актив.) | ||
| 1(13) | 0(1) | ||||