Тема 11. Арифметические и алгебраические основы выполнения вычислительных операций
Арифметические основы выполнения вычислительных операций
Прямой, обратный и дополнительный коды

1)Прямое кодирование

Прямой код используется для хранения информации, а также в устройствах ввода/вывода.

2) Обратный и дополнительный коды



если Х = +0,1011, то Хдоп = 0.1011
если Х = -0,1011, то Хдоп = 1.0100
Хдоп = Хобр + 2-n, где 2-n - младший разряд
Хобр = Хдоп - 2-n
Дополнительный код применяется в арифметико-логических устройствах, обратный код - при вводе/выводе.
При выполнении арифметических операций для чисел | X | > 1/2 может возникнуть переполнение разрядной сетки. В таком случае используются модифицированные дополнительный и обратный коды.
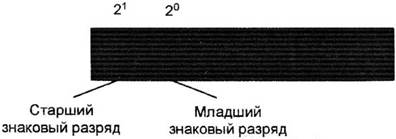

При выполнении арифметических операций в основном должен использоваться дополнительный код (операции с отрицательными числами), поэтому нужно осуществлять операцию преобразования в дополнительный (модифицированный) код.
Умножение в вычислительных машинах
Алгоритм умножения (основной) состоит в том, что производится операция суммирования множимого с частичным произведением в сумматоре и сдвигом множителя в ту или иную сторону. Эта операция повторяется n раз, где n - число разрядов множителя.
Четыре различных алгоритма умножения
1) Алгоритм умножения начиная с младших разрядов множителя при неподвижном множимом (для чисел с фиксированной запятой).

1-ый вариант - младшие разряды результата записываются в освободившиеся старшие разряды множителя.
2-ой вариант - младшие разряды результата записываются в расширенную часть сумматора частичных произведений.
2) Алгоритм умножения начиная с младших разрядов множителя при неподвижном сумматоре частичных произведений (для чисел с фиксированной запятой).

3) Алгоритм умножения начиная со старших разрядов множителя при неподвижном множимом.

4) Алгоритм умножения начиная со старших разрядов множителя при неподвижном сумматоре частичных произведений.

Основные алгоритмы деления в вычислительных машинах
Деление выполняется путем вычитания делителя из делимого, а затем из получающихся частичных остатков. Применяется операция сдвига. Предполагается, что мы работаем с числами с фиксированной запятой и делимое больше делителя Если в результате вычитания делителя из делимого оказывается, что полученный остаток больше единицы, то в соответствующий разряд частного записываем нуль, если же меньше единицы, то - единицу.
В операциях вычитания используется дополнительный код. Вычитание заменяется сложением. Тогда частичный остаток может получиться положительным или отрицательным.
Два алгоритма деления:
1) деление с восстановлением частичного остатка
2) деление без восстановления частичного остатка
Первый из этих алгоритмов используется редко.

Заносим в сумматор делимое, а в регистр делителя - делитель. Преобразуем делитель в дополнительный код. Производим сложение делимого с делителем в дополнительном коде.
1) 2а-b Остаток восстанавливаем
а - остаток
b - делитель
2) а-b Остаток не восстанавливаем
2(а-b)
2(a-b)+b
2a-b
Не используется такт восстановления на каждом разряде.
Пример:
С восстановлением

1 такт. Сдвиг делимого влево на один разряд + дополнительный код делителя:

2 такт. Восстановление остатка (к остатку прибавляем делитель):

3 такт. Сдвиг восстановленного остатка влево на 1 разряд + дополнительный код делителя:

Без восстановления

1 такт. Сдвиг делимого влево на один разряд + дополнительный код делителя:

2 такт. Сдвиг остатка на 1 разряд влево + делитель:

3 такт. Сдвиг остатка влево на 1 разряд + дополнительный код делителя:
