Тема 2. Логические основы теории автоматов
Логической функцией Y называется функция, которая принимает двоичные значения на множестве двоичных аргументов.
y=f(x1, x2,..., xn)- логическая функция
- количество различных функций
n=1, К=4 у1 = 0 у2 = 1 у3 = x у4 = x
n=1, К=16 …
Алгебра логики оперирует базовыми функциями.
Существует так называемая система прямой логики, где основными являются три функции:
1. y1 = х1 • х2 - конъюнкция (логическое умножение);
2. у2 = xl V x2 - дизъюнкция (логическое сложение);
_
3. у2 = х - инверсия (логическое отрицание).
С помощью этих функций можно выразить любую сколь угодно сложную функцию.
Логические элементы первых вычислительных машин реализовывались с помощью системы прямой логики.
Недостатки: физическая реализация требует три логических элемента.
Конъюнктор
Дизъюнктор
Инвертор
С появлением интегральных микросхем логические элементы стали иметь более сложный характер.
Система инверсной логики
отрицание конъюнкции
отрицание дизъюнкции
В этой системе используются два логических элемента: И-НЕ, ИЛИ-НЕ
Достоинства:
1. Всего два элемента.
2. Отрицание стоит на выходе, что усиливает сигнал на выходе. Это позволяет подключать к данному элементу большое количество других элементов (по сравнению с прямой логикой).
Способы задания логических функций.
1. Табличный способ
Таблица, с помощью которой задается логическая функция, называется таблицей истинности.
2. Аналитический способ
Совершенная дизъюнктивная нормальная форма (СДНФ)
где х - логическая переменная, а - степень аргумента
|
|
Совершенная - это форма, при которой в каждую конъюнкцию входят все n переменных.
Пример
СДНФ:
ДНФ:
Правила перехода от табличной формы к СДНФ
1. В таблице истинности выбираем те наборы, где функция равна 1;
2. Для этих наборов записываем конъюнкцию;
3. Если переменная равна 0, то она в эту конъюнкцию входит с отрицанием, если равна 1 - то в прямом значении.
Совершенная конъюнктивная нормальная форма (СКНФ)
где х - логическая переменная, а - степень аргумента
Правила перехода от табличной формы к СКНФ
1. В таблице выбираем наборы, где функция равна нулю;
2. Для каждого набора записывается дизъюнкция переменных;
3. Если переменная равна 1, то она записывается с отрицанием, если переменная равна нулю - в прямом значении.
Пример
Непрерывная логика.
1. Логическое умножение
x1, x2- непрерывные входные сигналы
у - непрерывный выходной сигнал
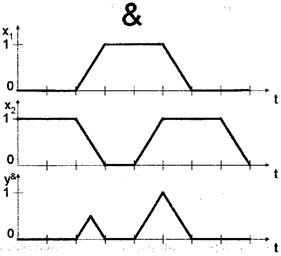
Из двух величин, поступающих на вход элемента, на выходе появляется минимальная.
2. Логическое сложение
x1, х2 - непрерывные входные сигналы у - непрерывный выходной сигнал
Из двух величин, поступающих на вход элемента, на выходе появляется максимальная.
Непрерывная логика используется в дискретных автоматах для анализа переходных процессов, которые происходят при наложении фронтов.
Минимизация логических функций. Метод диаграмм Вейча.
1. Переменная хi является несущественной переменной, если при изменении ее значения на противоположное функция остается прежней:
|
|
_
2. Склеивание: xi V xi = 1.
1). Для двух переменных
Склеиваются те клетки, которые имеют рядом стоящие единицы.
Диаграмма Вейча Результат склеивания
2). Для трех переменных
Если в диаграмме Вейча рядом стоит четыре единицы, то такое склеивание приводит к зависимости от одной переменной.
3). Для четырех переменных
Если рядом стоят восемь единиц, то функция зависит от одной переменной, четыре - от двух, две - от трех.
Диаграммы Вейча удобно использовать для не полностью определенных функций.
Пример
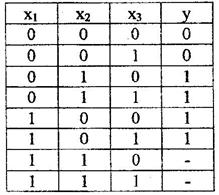
Вместо неопределенных значений функции поставим, где это удобно, единицы для того, чтобы склеить их как можно больше. Получим конечную функцию: 
Примечание: в реальных схемах не полностью заданные функции получаются тогда, когда некоторые комбинации двоичных входов являются запрещенными, либо они не могут быть поданы на вход схемы в силу особенностей работы логического элемента.