Надежность систем с последовательным соединением элементов

Надежность. Проектирование

Введение

В общем случае изделие состоит из отдельных систем, отличающихся функционально, то есть по решающим задачам. Для оценки надежности изделия требуется оценка надежности отдельных систем. Анализ работоспособности отдельных систем, не зависимо от функционального многообразия, показывает, что возможно подразделение на два основных класса:

1)системы с последовательным соединением элементов,

2)системы с параллельным соединением элементов.

Система с последовательным соединением элементов изображается графически в виде последовательной цепочки элементов.

Отказ любого элемента приводит к обрыву последовательной цепочки, т.к. вход и выход имеют одно единственное соединение.

Поэтому система с последовательным соединением элементов отказывает при условии отказа только одного из составных элементов.

Таким образом, функционал отказавшего элемента не возмещается другими элементами.

Система с параллельным соединением элементов изображается графически в виде параллельной цепочки элементов.

Отказ любого элемента не приводит к обрыву параллельной цепочки, т.к. вход и выход имеют множественное соединение.

Поэтому система с параллельным соединением элементов отказывает при условии отказа только всех из составных элементов.

Таким образом, функционал отказавшего элемента возмещается другими элементами.

Надежность систем с последовательным соединением элементов

Согласно определению, надежность системы с последовательным соединением элементов характеризуется вероятностью функционирования только всех из составных элементов:

Н=P{ρ₁(t)>0…ρ_n(t)>0; 0<t<T}

где ρ_i(t) – функции работоспособности элементов, Т – время функционирования системы.

Предположим, что функции работоспособности элементов системы являются случайными величинами. Тогда надежность системы может быть выражена через многомерный дифференциальный закон распределения случайных величин ρ₁, ρ₂…ρ_n:

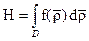где D – область интегрирования, определяемая системой неравенств ρ_i>0, i=1,2…n.

Для практических расчетов определим приближенные оценки надежности. Рас­смотрим вывод на примере системы из двух элементов.

Надежность данной системы представляется в виде:

H=P{ρ₁>0, ρ₂>0}

Тогда по теореме умножения вероятностей:

H=P{ρ₁>0}P{ρ₂>0|ρ₁>0}

Для случая независимых элементов:

H=P{ρ₁>0}P{ρ₂>0}=h₁,h₂

где h_i=P{ρ_i>0} – надежность элементов.

Для случая зависимых элементов:

H=P{ρ₂>0|ρ₁>0}

Рассмотрим линейную зависимость элементов:

ρ₂=aρ₁+b

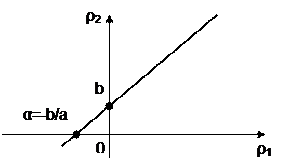Как видно из графика, при ρ₁>0 (функционирование первого элемента) получаются значения ρ₂>0 (функционирование второго элемента). Таким образом, условная вероятность P{ρ₂>0|ρ₁>0} равна единице, как вероятность достоверного события.

Тогда:

H=P{ρ₁>0}=h₁

Как видно из графика, при ρ₁<0 (отказ пер­вого элемента) на участке α<ρ₁<0 получаются значения ρ₂>0 (функционирование второго элемента).

Следовательно, второй элемент имеет более высокую надежность.

Тогда:

H=min{h₁,h₂}

По итогу двух рассмотренных случаев:

(h₁,h₂)≤H≤min{h₁,h₂}

В общем для системы с произ­вольным числом элементов:

где h_i – надежность элементов.

Равенство справа выполняется для случая линейной зависимости элементов (коэффициент корреляции r=1), равенство слева выполняется для случая независимости элементов (коэффициент корреляции r=0). При промежуточных значениях коэффициента корреляции надежность стоит внутри диапазона.

Оценим характер измене­ния надежности в зависимости от коэффициента корреляции на при­мере. Рассмотрим систему из двух равно-надежных элемен­тов h₁=h₂=h₀, Пусть функции работоспособности элементов подчине­ны нормальному закону распределения.

График изменения надежности системы зависимых элементов в зависимости от коэффициента корреляции для различных значений надежности элемента представлен на рис.

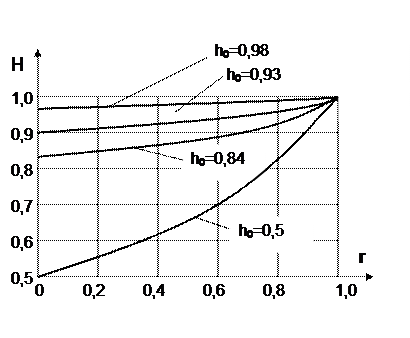
Как видно из графика, для случая зависимых элементов с увеличением коэффициента корреляции надежность системы повышается и при r=1 достигает максимального значения, равного надежности одного элемента.

График изменения надежности системы независимых элементов в зависимости от числа элементов представлен рис.

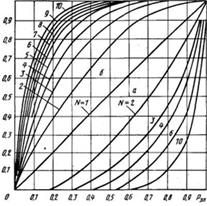
Как видно из графика, для случая независимых элементов при последовательном соединении (а) с увеличением числа элементов надежность системы понижается.

Как видно из графика, для случая независимых элементов при параллельном соединении (б) с увеличением числа элементов надежность системы повышается.