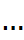Основные Правила Комбинаторики
1.1 Правила Сложения
Определение: Пусть есть множество объектов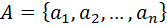 
и
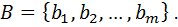Количество способов выбрать один объект из 
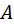или один объект из 
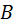равно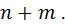 
Пример: Пусть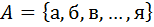 
и пусть 
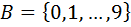. Тогда
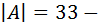(количество элементов в множестве 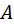, то есть мощность множества 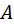). Поэтому 
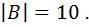И из правила сложения следует, что количество способов выбрать либо одну букву, либо одну цифру равна
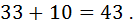
Правила Умножения
Определение: Пусть есть множество объектов 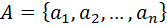и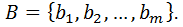 
Количество способов, выбрать сперва ровно один объект из 
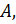а вслед за ним ровно один объект из 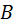равно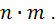 
Следствие. Пусть есть множество объектов 
и пусть
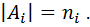Тогда число способов извлеч сперва один объект из множества 
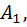поставить вслед за ним один объект из множество 
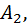расположить за ним ещё один объект из множество 
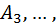и всю эту цыпочку последовательно извлекаемых объектов завершить ровно одним объектом из 
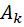равно 
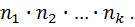
Пример: Рассмотрим автомобильные номера вида K125MX и найдем их количество. Пусть у нас будет такая(типа) схема:
K 1 2 5 M X
 | |||
 | |||
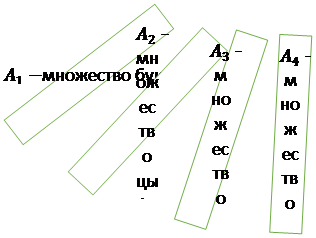Пусть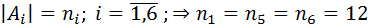 
(12 букв таджикского алфавита имеют аналоги в латыне); И ещё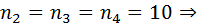 
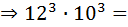количество номеров вида K125MX;
Задача: Есть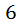 
человек среди которых 
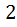девушки. Эти 
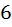человек пришли в большой театр и хотят рассесться в ложи. И всего в ложи 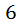мест. Сколько существует различных способов рассадить товарищей по вот этим шести местам в ложи, если девушки не должны сидеть с краю?
Решение: Мы знаем, что есть 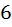лож:; Давайте рассадим людей сначала на краях ложи. На краях ложи могут только сидиться мальчики. По правилу умножения края ложи можно рассадить мальчиками 
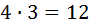способами. Края ложе как бы уже занято, поэтому теперь рассадим людей в оставщихся 
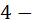местах. В этих оставщихся местах можно рассадить две остальных мальчиков и две наших девушек, то есть четырех человек. Значит по правилу умножения количество таких рассадок равно 
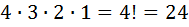способов. А количество способов всех рассадок, то есть рассадок по всем шести ложам равен 
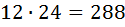способов – по правилу умножения, так как внутренные и крайные рассадки были сделаны последовательно, то есть один вслед за другим. Ответ: 
.
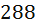Задача: Есть пароль компьютера. И этот пароль состоит из цифр и маленьких букв латинского алфавита.
a) Сколько существует таких паролей длины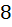 
?
b) Сколько таких паролей длины 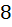, если в каждом из них обязательно присутствует хотя бы одна цифра?
c) Сколько таких паролей длины 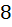, если в них есть совпадающие символы?
Решение:
a) Понятно, что цифр на свете имеется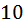 
штук, и понятно, что маленькие буквы латинского алфавита 
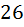штук. Значит итого 
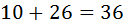символов, каждый из которых мы вольны поставить на любую позицию нашего будущего пароля. Ну на первую позицию пароля мы можем поставить любую из 
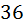символов. Соответственно мы на вторую позицию можем спокойно поставить любое из 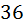символов, и естественно поскольку мы это сделаем вслед за тем, как что то выбирали для первой позиций, то мы пользуемся правилом умножения 
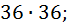На третью позицию у нас снова есть 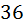возможности того, что поставить, поскольку это сделается вслед за 
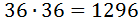возможности которые уже перечислены (в первых двух позициях), то надо снова эти умножить 
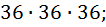Ну итак далее, …, умножаем и умножаем по куду не исчерпаются все наши позиции, каковых в нашей задачи 
штук. То есть на каждую позицию можно поставить символы любим из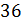 
способов, и мы получаем 
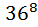способов. Ответ: 
;
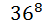b) Давайте найдём число паролей без цифр. Значит если мы не используем цифры, то это просто означает, что на каждую позицию имеется ни 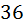символов, а только 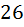. Ну естественно количество паролей без цифр равно 
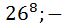это ровно по тому же принципу по которому 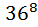было в пункте a); Ну так мы нашли число паролей без цифр. А число всех паролей-это 
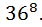Следовательно число паролей которые содержат хотя бы одну цифру – это разность общего числа паролей и числа паролей которые цифру не содержат, то есть
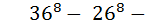наше искомое число. Ответ: 
;
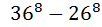c) Сначала найдем количество тех паролей, в которых все символы различны. Мы можем на первую позицию этого пароля поставить любой из 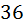символа, то есть на первую позицию у нас есть 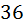возможности. А на вторую позицию (когда уже выбран какой то символ для первый) у нас остаётся только 
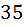возможности, потому что мы считаем такие пароли у которых символы не совпадают, то есть на вторую позицию мы обязаны выбрать какую то новый символ. Ну и дальше рассуждая точно также на третью позицию у нас остаётся 
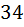возможностей, потому что мы уже выбрали два разных символа на первые две позиции нашего пароля. И так на четвертую позицию остаётся 
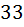возможности; на пятую 
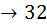; на шестую 
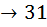; на седьмую 
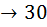; и на восьмую 
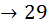; Ну по правилу умножения количество паролей у которых символы не совпадают равен 
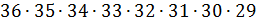; И если от общего числа паролей отнять число паролей в которых нет совпадающих символов, мы найдём количество паролей в которых есть совпадающие символы, то есть это количество равно
;
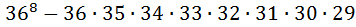Ответ: .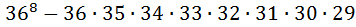
Принцып Дирихле
Определение: Есть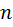 
ящиков и 
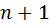кроликов. Как не рассаживай кроликов по ящикам, найдется ящик в котором хотя бы 
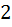кроликов.
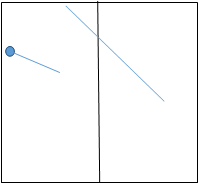
Пример: У нас есть квадрат со стороной 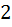, и в этом квадрате берём 
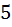точек. Как бы 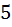точек ни были расположены внутри квадрата со стороной 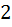, найдутся два из них на расстоянии 
.
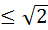Решение: Давайте перерисуем квадрат со стороной 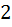, и разобъём его на 
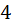клеточки (ящиков) со стороной 
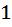. Тогда получиться, что как ни бросай 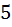точек (кроликов) по клеточкам (ящикам), объязятельно найдется хотя бы одна клеточка в которую попадает не меньше 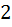точек (кроликов). А если 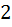точки попадали внутрь одной клетки, то конечно расстояние между ними не превосходит длины диагонали этой клетки, потому что диагональ-это самое большое расстояние внутри клетки. Ну а длина диагонали по теореме Пифагора 
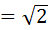. То есть получается, что те две точки которые мы нашли в нашей клеточки (в нашем ящике) – они удалены друг от друга на расстоянии не превосходящее 
.
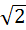2
 |
2
Задача: Есть монеты стоимостью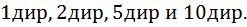 
Какое минимальное количество таких монет необходимо и достаточно взять, чтобы с гарантией среди вот этих взятых монет нашлось 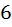монет одного достоинство?
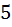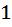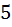Решение: Действително мы можем взять монет достоинством дир, монет достоинством 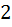дир, 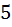монет достоинством 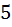дир, и, 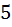монет достоинством 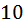дир. При этом в сумме получается, 
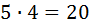монет, и среди них нет шестёрки одинаковых. Но нам необходимо и достаточно взять так чтобы с гарантией среди взятых монет нашлось 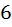монет одного достоинство. Это означает, что либо монет с достоинством 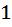дир не меньше шести, либо монет с достоинством 
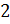дир не меньше шести, либо монет с достоинством 
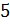дир не меньше шести, и либо монет с достоинством 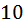дир не меньше шести, то есть какая то шестёрка уже точно найдётся. Следовательно, если уже какая то шестёрка есть, значит нам необходимо и достаточно взять 
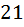монет, чтобы среди них нашлось 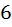монет одного достоинство.
Ответ: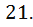 
Задача: Есть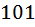 
пуговица одного из 
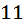цветов. Докажите, что либо найдется 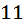пуговиц одного цвета, либо найдётся 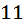пуговиц все цвета которых разные.
Решение: Давайте действуем методом от противного. Предположим неверно ни первое утверждение, ни второе утверждение, то есть предположим, что нет 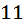пуговиц одного цвета, и нет 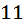пуговиц разного цвета. Давайте прежде всего привяжемся ко второму предположению. То есть что значит, что нет 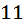пуговиц разного цвета? –Это в на самом деле означает, что среди наших 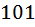пуговиц все 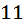цветов не задействованы. Следовательно из этой предположений выходит, что задействованы не более чем 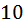цветов. Теперь давайте посмотрим на первое предположение, то есть, нет 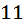пуговиц одного цвета. Это означает, что пуговиц каждого конкретного цвета не больше 
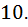И используя выводы которые мы нашли в наших двух предположениях следуем так: Задействовано не больше чем 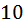цветов, т.е, есть(имеем) сколькото пуговиц первого цвета, есть сколькото пуговиц второго цвета,..., и так далее,...,номер 
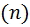последнего цвета не превосходит десяти, то есть сколько то пуговиц какого то цвета и вот
номер 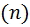этого какого то цвета не превосходит десяти. Ну мы говорим, что есть сколько то пуговиц первого цвета, есть сколько то пуговиц второго цвета, …, сколько то пуговиц последнего цвета номер 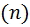которого не превосходит десяти, а мы ещё знаем, что пуговиц каждого цвета не больше десяти. Давайте приведём рисунок и в этом рисунке номера цвета пуговиц–это числа от 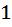до 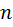. А каждый пуговиц не больше десяти:
1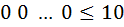 
(Пуговиц первого цвета, их не больше )
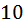2 (Пуговиц второго цвета, их не больше )
(Пуговиц последнего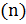 
цвета, их не больше 
)
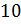И так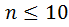 
(номер последнего цвета), то получается, что суммарная количество пуговиц в нашем распоряжении 
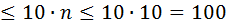, то есть не больше чем 
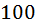–это противоречие, ведь мы знаем, что у нас 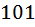пуговица. Значит наши предположении были неправильными. ЧТД.
Задания
Вопрос 1
Автомобильные номера штата Калифорнии состоят из одной цифры, не равной 0, трёх больших букв латинского алфавита и ещё трёх цифр (например,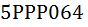 
). Сколько всего имеется номеров такого типа?
Вопрос 2
Путешественнику нужно добраться из города 
в город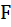 
двигаясь каждый раз вправо или вверх по стрелкам (см. карту). Сколькими способами это можно сделать?
Вопрос 3
В мешке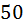 
шаров, отличающихся только цветом: 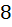красных, 
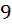синих, 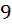желтых, остальные – поровну черные и белые. Какое наименьшее число шаров надо вынуть из мешка, не видя их, чтобы среди них гарантированно было не менее 
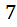шаров одного цвета?
Вопрос 4
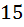футбольных команд (в каждой по 
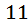человек) летят из Москвы в Душанбе на соревнования. Какое минимальное количество мест может быть в самолете, чтобы гарантированно нашлась команда, долетевшая в полном составе?
Вопрос 5
Сколько чисел от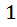 
до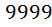 
(включая 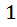и 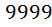) не имеют в своей десятичной записи одинаковых подряд идущих цифр? (к примеру, не подходят 
).
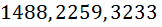Вопрос 6
У вас есть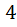 
ящика и 
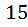кроликов. Какие утверждения являются верным?
а)При любой рассадке кроликов по ящикам найдётся ящик, в котором будет сидеть по крайней мере 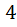кролика.
б)При любой рассадке кроликов по ящикам найдётся ящик, в котором будет сидеть по крайней мере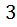 
кролика.
в)При любой рассадке кроликов по ящикам найдётся ящик, в котором будет сидеть по крайней мере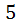 
кроликов.
г)При любой рассадке кроликов по ящикам найдётся ящик, в котором будет сидеть по крайней мере 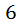кроликов.
Вопрос 7
Имеется 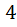банки желтой краски, 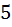банок синей краски и 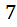банок красной краски, все банки разного размера. Какие утверждения являются верным?
а)Банку краски можно выбрать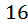 
способами.
б)По одной банке каждой краски (
желтую, синюю, красную) можно выбрать 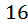способами.
в)По одной банке каждой краски (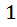 желтую, 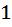синюю, 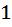красную) можно выбрать 
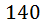способами.
г)Банку краски можно выбрать 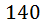способами.
Ответы:
Основные Комбинаторные Величины
|
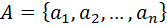Пусть дан множество .Давайте представим себе, что каждый из этих элементов нарисовано на некоторой карточке:
Тепер рассмотрим два видов коробок. Первого коробка назовем “обычная коробка”, и второго коробка назовем “божественная коробка”. Для каждых из этих коробок рассмотрим по два разных вариантов. Давайте первые два варианта рассмотрим для обычной коробки, а остальные два варианта рассмотрим для божественной коробки. Давайте начнем для обычной коробки первые два варианта:
Обычная Коробка
Вариант: Зачерпываем в пригоршни -элементов из обычной коробки.
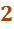Вариант: Последователно извлекаем элементы из обычной коробки, и получаем на выходе определенную кучку из 
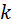-элементов. И нам очень важен порядок извлекаемых объектов.
Мы рассмотрели все варианты обычной коробки. Надо добавить, что когда мы рассмотрели вариантов обычной коробки, у нас количество элементов было -штук. Свойство божественной коробки отличается от свойство обычной коробки. Разница в том, что в божественной коробки не содержится -элементов, а содержится бесчисленное множество элементов, и все виды элементы божественной коробки совпадают с элементами обычной коробки. Божественная коробка содержит бесчисленное множество карточек. Т. е есть бесчисленное множество карточек на которых нарисовано элемент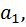 
есть бесчисленное множество карточек на которых нарисовано элемент 
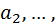есть бесчисленное множество карточек на которых нарисовано элемент 
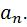То есть у нас есть -бесчисленных множеств, и все они запихнуты в эту божественную коробку. Давайте начнем рассмотреть два варианта божественной коробки.
Божественная Коробка
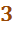Вариант: Зачерпываем в пригоршни -элементов из божественной коробки.
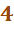Вариант: Последователно извлекаем элементы из божественной коробки, и получаем на выходе определенную кучку из 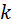-элементов. И нам очень важен порядок извлекаемых объектов.
И так мы рассмотрели всех вариантов. Теперь каждому варианту даем определенное название.
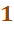Вариант: -сочетания без повторений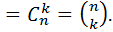 
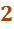Вариант: -размещения без повторений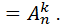 
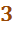Вариант: -сочетания с повторениями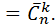 
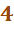Вариант: 
-размещения с повторениями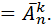 
Теорема: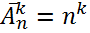 
.
Доказательство: 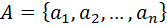. На первую позицию в будущем 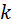-размещении с повторениями, мы можем выбрать любой из этих
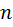-объектов. На вторую позицию в -размещении мы тоже можем выбрать любой из наших 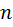-объектов. …. На 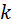-ю позицию мы тоже можем выбрать любой из наших 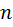-объектов. Но понятное дело, что количество таких размещений с повторениями и будем вычислять как:
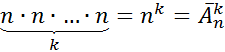. ЧТД.
Теорема: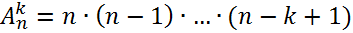 
.
Доказательство: На первую позицию в 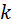-размещений без повторений мы можем выбрать любой из 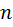-объектов. На вторую позицию в -размещений без повторений мы можем выбрать любой из оставщихся 
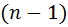-объектов..... На 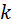-ю позицию в 
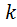-размещений без повторений мы можем выбрать любой из оставщихся 
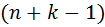-объектов. По правилу умножения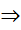 
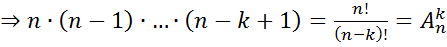. ЧТД.
Следствие: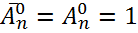 
.
Доказательство: Ну почему это так? – Это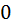 
-размещений 
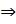мы нечего не размещаем 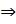мы просто нечего незделаем. Но сколькими способами можно выташить так сказать пустое множество объектов? - И понятное дело, что можно сделать 
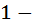способом. И даже, если в формулах поставить будет тоже верно, то есть 
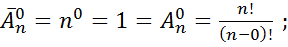ЧТД.
Следствие: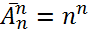 
;
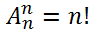( Число перестановок ).
Доказательство: Что значит выбрать -объектов из множество мощности 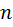?. Что значит выбрать с учетом последовательности, с учетом порядка? Ну нашы формулы нам дают следующее:
;
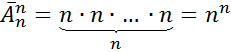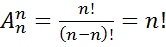(число различных всевозможных перестановок). ЧТД.
Задача: На пиратском корабле есть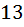 
человек экипажа. Сколько существует различных способов выбрать из этих 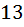человек капитана и боцмана ему в помощнике?
Решение: Давайте обозначим людей как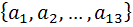 
. Из этого множество из 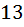объектов нам нужно выбрать два объекта без повторений. И здесь при выборе объектов речь идёт о размещении, так как нам важен порядок следований объектов внутри нашей пары которую мы выбираем. То есть это должны быть два разных объекта, и порядок их нам важен, потому, что важно какие именно должности эти два товарищи будут иметь – кто из них капитан, а кто из них боцман. Поэтому это в чистом виде два размещения без повторений из 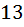объектов, то есть 
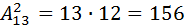различных способов составить из 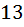член экипажа пару капитана и боцмана.
Ответ: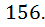 
Задача: Имеется игрушечный поезд. Он состоит из 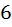вагонов. А в наборе к этому игрушечному поезду имеется 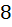типов вагонов (плацкартные, купейные, ресторан, …).
а) Сколько всего существует способов составить поезд, если все вагоны в этом поезде были разными?
б) Сколько есть способов составить поезд, если все вагоны в этом поезде были различными и в этом поезде обязательно есть вагон ресторан?
Решение:
а)Мы должны составить поезд из 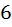вагонов. И здесь у нас речь идёт о выборе. Ну понятное дело, мы выбираем из множество который состоит из 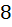элементов(вагонов) 
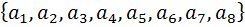. И надо выбрать их ровно 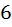штук из этой множестве который состоит из 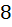элементов, и все вагоны должны быть разными. Значить наш выбор – это размещение без повторение, то есть 
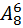способов.
б) Выбираем позицию для вагонов ресторан. Это естественно делается шестью способами. После чего у нас остается 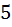позиций. И из 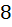типов вагонов который у нас были в нашем распоряжении, остаётся только семь типов вагонов которыми можно пользоваться. Следовательно количество способов который нам нужен, равен 
;
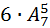Ответ: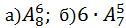 
.
Задача: Маша и Петя подумали некий язык, в котором символы,,.
а) Сколько существует различных слов из пяти букв?
б) Сколько можно составить слов, у которых длина не больше пяти?
в) Сколько можно составить слов из не более пяти букв, если первая буква – эта обязательно?
Решение:
а) Понятно, что речь идет о повторении. То есть три объекта, и из них мы выбираем какие то угодно 5, при этом возможно повтор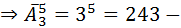 
различных слов из пяти букв которое можно составить на языке Маши и Пети;
б) Мы уже знаем сколько есть слов каждый из которых состоит из ровно пяти букв – эта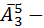 
слов; Дальше мы можем совершенно аналогично посчитать количество слов в каждом из которых ровно четыре буквы – эта 
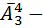слов. Дальше мы посмотрим на слова которые содержат всего три буквы – эта 
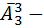слов; Посмотрим две буквы – эта 
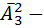слов. И наконец одна буква– эта 
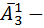слов. Значить количество слов длина которых не более пяти букв, равен 
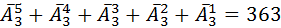слов.
в) Давайте рассмотрим сначала сколько можно составить слов длины пять (в нашем случае). Ну мы знаем, что первая буква – эта, значить надо заполнить оставшихся четыре позиции в этом пятибуквенном слове.; Это можно сделать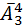 
способами. Дальше найдем количество слов длины четыре – эта аналогичным образом будет 
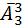слов. Дальше найдем количество слов длины три – эта сделается 
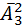способами. Дальше количество слов длины два – эта 
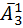способов. И наконец количество слов длины один – эта делается 
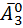способами. 
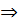Итого мы получим 
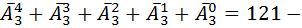количество слов которые не более пяти букв имеют в своем записи, и первая буква которых. 
Задача: Есть три студента –Марям, Салва и Хатиджа. Они собираются на свадьбу. Им необходимо нарядится. И у них есть в распоряжении некоторые количество разных нарядов – 4рубашки, 3джинсы, и 8пар обуви. Сколькими способами они могут распределить между собой эти самые наряды, так чтобы по-разному нарядиться для свадьбы?
Решение: Давайте сначала рассмотрим рубашки, и обозначим их как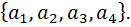 
Из этих четырех объектов надо выбрать три распределяя по разным студентам. Ну естественно – три размещения без повторений, потому что порядок исключительно важен и рубашки все разные. То есть количество способов раздачи рубашек – эта 
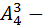способов. И тоже самое касается ситуации с раздачи джинсы – 
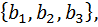то есть 
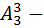способов. И тоже самое с ситуации которое касается пар обуви – 
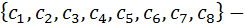это сделается 
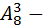способами. Итого по правилу умножения получается, что количество способов распределения между студентами эти самые наряды, так чтобы по-разному нарядиться для свадьбы равен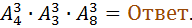 
Теорема: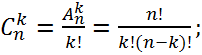 
Доказательство: Пусь у нас есть множество состоящий из 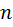-объектов 
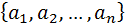. Из этого множество мы извлекаем всевозможные -сочетаний без повторений. Берём какой ни будь -сочетаний без повторений. Нарисуем его как прямоугольник, и рядом пищем элементы этой сочетаний, а внутри пищем номер данной сочетаний:
{ 
}
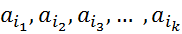(множество элементов этой конкретной сочетаний)
Потом ещё какую ни будь другую -сочетаний возмëм:
{ 
}
{ 
}
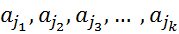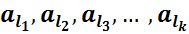Последний прямоугольник (наш 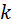-сочетаний без повторений) имеет номер 
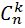, так как все эти прямоугольники показывают количеству всех конкретных 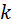-сочетаний без повторений. И номер всех сочетаний –это и есть количество всех возможных 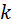-сочетаний, то есть равен номеру последней прямоугольника. Теперь элемент каждого прямоугольника переставляем. И это у каждого прямоугольника 
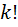–различных размещений отвечающих данному сочетанию. А сколько всего размещений? – Очевидно, что всего 
размещений. То есть получается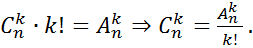 
ЧТД.
Теорема: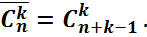 
Доказательство: Пусть у нас есть какой-то набор объектов {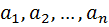 
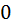}. Из этих объектов мы составляем всевозможные -сочетания с повторениями. Каждому из этих -сочетаний с повторениями мы сопоставляем паспорт с номером и 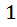, другими словами мы закодируем наш паспорт. Мы просто рисуем в начале столько единиц, сколько раз в данном конкретном -сочетании встречается элемент 
: 
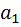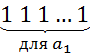
И не рисуем единицы вовсе, если 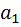в данном конкретном -сочетаний (которое мы пытаемся закодировать) просто не встречается. Дальше рисуем перегородку в виде 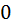отделяющего встречаемого элемента