МИНЕСТЕРСТВО СЕЛЬСКОГО
ХОЗЯЙСВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ
ОБЩЕОБРОЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
Кафедра высшего математики и физики
Реферат 1
Тема:Поток вектора напряженности электрического поля.Теорема Гаусса и ее применение к расчету электрических полей. Дифференциальная формулировка теоремы Гаусса
Выполнил
Анисимов Д.Ю.
Проверил
доц к.ф.-
м.н. Иванов В.П.
Москва 2017
Поток вектора напряженности
Определим поток вектора 
через произвольную поверхность dS, 
- нормаль к поверхности.α - угол между нормалью и силовой линией вектора . Можно ввести вектор площади 
. ПОТОКОМ ВЕКТОРА называется скалярная величина ФЕ равная скалярному произведению вектора напряженности на вектор площади 
Для однородного поля
Для неоднородного поля
где 
- проекция на , 
- проекция на .
В случае криволинейной поверхности S ее нужно разбить на элементарные поверхности dS, рассчитать поток 
через элементарную поверхность, а общий поток будет равен сумме или в пределе интегралу от элементарных потоков
где 
- интеграл по замкнутой поверхности S (например, по сфере, цилиндру, кубу и т.д.)
Поток вектора 
является алгебраической величиной: зависит не только от конфигурации поля , но и от выбора направления . Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т.е. нормаль, направленная наружу области, охватываемой поверхностью.
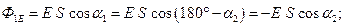
Для однородного поля поток через замкнутую поверхность равен нуля. В случае неоднородного поля
.
Теорема Гаусса и ее применение к расчету напряженности электростатического поля
I. Рассмотрим электростатическое поле, создаваемое единичным положительным зарядом. Заключим его в сферу радиуса R. Определим поток напряженности 
через сферическую поверхность радиуса R.
Разобьем поверхность S сферы на элементарные площадки dS. Нормаль к площадке dS направлена по линии радиуса сфера и совпадает с направлением вектора : 
параллельна поэтому
Тогда поток вектора через поверхность S будет равен сумме потоков через элементарные площадки dS и устремляя dS к 0 можно записать, что
Учитывая, что напряженность поля точечного заряда равна
получим
Этот результат можно обобщить на случай любой поверхности.
Учитывая принцип суперпозиции можно полученный результат применить к любому количеству зарядов, находящихся внутри поверхности.
ТЕОРЕМА ГАУССА:
Поток вектора напряженности через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0 (ε0 - электрическая постоянная)
II. Применение теоремы Гаусса.
1. Напряженность поля, создаваемая бесконечно протяженной однородно заряженной плоскоти с поверхностной плотностью заряда σ.
ПОВЕРХНОСТНАЯ ПЛОТНОСТЬ ЗАРЯДА показывает, какой заряд приходится на единицу площади 
Пинии напряженности перпендикулярны рассматриваемой поверхности и направлены от нее в обе стороны. Построим цилиндр с основанием S, образующая которого параллельна линиям напряженности .
Так как образующая цилиндра параллельна 
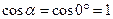, то поток через основание S равен
Поток через боковую поверхность цилиндра равен нулю, т.к. перпендикулярна S cosα= cos90° = 0, следовательно,
2. Напряженность поля, создаваемая двумя параллельными бесконечно протяженными пластинами с поверхностной плотностью зарядов +σ и -σ. Найден поле Е, используя принцип
суперпозиции полей. В области между плоскостями
Слева и справа от плоскостей поля вычитаются, т.к. линии напряженности направлены навстречу друг другу 
.
3. Напряженность ноля, создаваемая бесконечно протяжённой нитью с линейной плотностью заряда τ.
Линейная плотность заряда показывает, какой заряд приходится на единицу длина проводника.
Требуется определить напряженность ноля на некотором расстоянии r от нити. Для этого построим цилиндр радиуса r и высотой h, по оси которого проходит нить.
Поток через основания рассматриваемого цилиндра равен нулю, т.к. 
перпендикулярна вектору 
, следовательно, поток будет определяться только потоком через боковую поверхность цилиндра
4. Напряженность поля, создаваемого сферической поверхностью с поверхностной плотностью заряда σ.
На сфере радиуса R распределен заряд q. Поверхностная плотность заряда
Линии напряженности направлены радиально, отходя от поверхности сфера под прямым углом. Окружаем данную сферу сферой радиуса r и определяем поток напряженности через cферическую поверхность радиуса r.
При r > R весь заряд q попадает внутрь сфера r. Тогда по теореме Гаусса
, т.к. Е n = E.
При r < R внутри поверхности радиуса r зарядов нет и поэтому Е=0. На этом основано экранирование - защита от внешних электрических полей.
5. Напряженность поля объемно заряженного шара с объемной плотностью заряда ρ.
Объемная плотность заряда показывает, какой заряд приходится на единицу объема
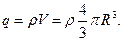
а) При r > R по пункту 4 находим
б) При r < R
