Введение
Функциональный анализ — раздел математики, в котором изучаются бесконечномерные пространства и их отображения.
Понятие нормированного пространства – одно из самых основных понятий функционального анализа. Теория нормированных пространств была построена, главным образом, С. Банахом в 20-х годах 20 века. Функциональный анализ за последние два десятилетия настолько разросся, настолько широко и глубоко проник почти во все области математики, что сейчас даже трудно определить самый предмет этой дисциплины. Однако в функциональном анализе есть несколько больших «традиционных» направлений, которые и поныне в значительной степени определяют его лицо. К их числу принадлежит дифференцирование линейных нормированных пространств.
Основные понятия
Определение 1. Непустое множество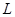 
называется линейным пространством, если оно удовлетворяет следующим условиям:
Й. Для любых двух элементов 
однозначно определен элемент 
, называемый их суммой, причем
1. 
(коммутативность)
2. 
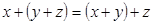(ассоциативность)
В 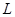существует такой элемент 0, что 
для всех 
4. Для каждого существует такой элемент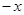 
, что 
.
II. Для любого числа 
и любого элемента определен элемент 
, причем
5. 
6. 
III. Операции сложения и умножения связаны между собой дистрибутивными законами:
7. 
8. 
Определение 2. Линейное пространство 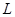называется нормированным, если на нем задана неотрицательная функция 
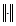, называемая нормой, удовлетворяющая условиям:
для любого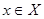 
и любого числа ;
для любых 
(неравенство треугольника).
Определение 3. Оператором называется отображение
,
где 
- это линейные пространства.
Определение 4. Оператор 
называется линейным, если для любых элементов 
и любых чисел 
R выполняется равенство:
Определение 5. Пусть - линейные нормированные пространства,
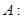
– линейный оператор,
Линейный оператор непрерывен в точке 
, если из того, что
следует, что 
.
Определение 6. Линейный оператор 
непрерывен, если он непрерывен в каждой точке 
.
Определение 7. Линейный оператор называется ограниченным, если
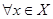
Утверждение. Для линейного нормированного пространства непрерывность линейного оператора равносильна его ограниченности.
Определение8. Наименьшая из констант M таких, что 
, называется нормой оператора А и обозначается 
.
В частности, выполняется
Справедливо следующее утверждение: для любого ограниченного линейного оператора
Сильный дифференциал (дифференциал Фреше)
Пусть X и У — два нормированных пространства и F — отображение, действующее из X в Y и определенное на некотором открытом подмножестве О пространства X. Мы назовем это отображение дифференцируемым в данной точке 
, если существует такой ограниченный линейный оператор Lx 
ж (X, Y), что для любого е> 0 можно найти д > 0, при котором из неравенства ||h||< д следует неравенство
|| F(x + h)-F(x)-Lxh ||<е||h|| (1)
То же самое сокращенно записывают так:
А(ч + р)-А(ч)-Дчр = щ(р)ю(2)
Из (I) следует, что дифференцируемое в точке х отображение непрерывно в этой точке. Выражение Lxh (представляющее собой, очевидно, при каждом h 
X элемент пространства У) называется сильным дифференциалом (или дифференциалом Фреше) отображения F в точке х. Сам линейный оператор Lx называется производной, точнее, сильной производной отображения F в точке х. Мы будем обозначать эту производную символом F'(x).
Если отображение F дифференцируемо в точке, то соответствующая производная определяется единственным образом. В самом деле, равенство
||L1h — L2h|| = o(h) для операторов
Li 
ж (X, У), i = 1, 2,
возможно, лишь если L1= L2.
Установим теперь некоторые элементарные факты, непоcредственно вытекающие из определения производной.
Если F(x) = y0 = const, то F'(x) = О (т. е. F'(х)
в этом случае есть нулевой оператор).
Производная непрерывного линейного отображения L есть само это отображение:
L '(x)=L(3)
Действительно, по определению имеем
L(x + h)-L(x) = L(h).
3. (Производная сложной функции). Пусть X, У, Z — три нормированных пространства, U(x0)—окрестность точки х0 Х, F — отображение этой окрестности в У, у0 = F(x0), V(yo) — окрестность точки у0 У и G — отображение этой окрестности в Z. Тогда, если отображение F дифференцируемо в точке хо, a G дифференцируемо в точке уо, то отображение Н = GF (которое определено в некоторой окрестности точки х0) дифференцируемо в точке хо и
H' (x0)=G' (y0)F' (x0) (4)
Действительно, в силу сделанных предположений
А(ч0 +о) = А(ч0) + Аэ (ч0) о +о1 (о) и
G (уо + з) = G (уо) + G' (уо) з + о2 (з).
Но F'(x0) и G'(yo) — ограниченные линейные операторы. Поэтому
H (х0 + о) = G (уо + F' (x0) о + о1 о) = G (уо) + G' (у0) (F' (х0) о + +о1 о)) +
+о2 (F' (x0) о + о1 (о)) = G (у0) + G' (уо) F' (х0) о + о3 (о).
Если F, G и Н — числовые функции, то формула (4) превращается в известное правило дифференцирования сложной функции.
4. Пусть F и G — два непрерывных отображения, действующих из X в Y. Если F и G дифференцируемы в точке х0, то и отображения F + G и aF (а — число) тоже дифференцируемы в этой точке, причем
(F + G)'(х0) = F'(х0) + G'(х0) (5)
(aF)'(x0) = aF'(x0).(6)
Действительно, из определения суммы операторов и произведения оператора на число сразу получаем, что
(F+G)(x0 + h) = F(x0 + h) + G(x0 + h) = F (х0) + G (х0) + F' (х0) h +
+G' (х0) h + o1 (h) и
aF (x0 + h) = aF (x0) + aF' (x0) h + o2 (h),
откуда следуют равенства (5) и (6).