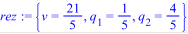Теория игр представляет собой комплекс математических моделей и логико – математический аппарат для анализа и разработки стратегий и принятия оптимальных решений в условиях конфликта интересов и неопределенности поведения. Изучение и использование инструментария теории игр становится неотъемлемой частью современного образования, поскольку теоретико – игровые подходы стали одним из основных инструментов экономического анализа. Теория игр, с одной стороны, сыграла ключевую роль в становлении современной теории оптимизации, а с другой – предлагает пути и методы решения сложных стратегических задач в самых различных областях.
Основными видами игр являются матричные, т.е. конечные парные игры с нулевой суммой.
Существуют различные методы решения матричных игр. Если игра имеет размерность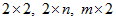 
, то для решения таких игр можно использовать графический метод. Известны приближенные методы решения матричных игр, – например, метод Брауна. Многие матричные игры сводятся к задачам линейного программирования, когда по заданной платежной матрице составляется пара взаимодвойственных задач, решение которых позволяет найти оптимальные стратегии и цену игры.
Основные разделы теории игр входят теперь в программы обязательных и специальных дисциплин («Исследование операций», «Методы оптимизации» и др.) для студентов различных направлений. При изучении раздела «Теория игр» могут быть использованы различные математические пакеты, такие как Maple, Рассмотрим применение математического пакета Maple при решении матричных игр. Это самый первый пакет символьной математики. В настоящее время он является лидером среди универсальных систем символьных вычислений и пользуется особой популярностью в научной среде и предоставляет возможности для математических исследований любого уровня.
Приведем некоторые примеры. В большинстве случаях, чтобы найти оптимальные стратегии в матричных играх приходится решать громоздкие задачи линейного программирования. В системе Maple имеется библиотека «simplex», предназначенная для решения задач линейного программирования с использованием симплекс-метода. Основные функции библиотеки – «maximize», «minimize» позволяют найти экстремумы линейной целевой функции при заданных ограничениях на изменение переменных. При этом студенты имеют возможность интерактивно изменять параметры модели и анализировать полученные решения.
Чтобы визуализировать решение, необходимо подключить графический пакет «plots». Команды этого пакета могут быть использованы студентами при изучении графического метода решения матричных игр. Тему «Игры с седловой точкой» можно визуализировать, используя команду «matrixplot». С помощью этой команды студенты могут построить 3D-график платежной матрицы игры и определить на нем седловую точку.
Рутинные вычисления среднего выигрыша при применении игроками смешанных стратегий, нахождение решений, возникающих в теоретико-игровых моделях линейных систем, и многие другие задачи можно выполнить при помощи команд пакета «linalg» (линейная алгебра).
Используя встроенный язык программирования [3], студенты могут писать собственные библиотеки процедур и функций и использовать их при изучении теоретико-игровых моделей.
Рассмотрим конкретные задачи.
Пример 1. « Предприятие выпускает три вида продукции (А, Б и В), получая при этом прибыль, зависящую от спроса. Спрос в свою очередь может принимать одно из четырех состояний (I, II, III, IV). В следующей матрице элементы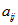 
характеризуют прибыль, которую получит предприятие при выпуске i -й продукции и k -м состоянии спроса. Определить оптимальные пропорции выпускаемой продукции, считая состояние спроса полностью неопределенным, гарантируя при этом среднюю величину прибыли при любом состоянии спроса» [4].
| I | II | III | IV |
| А | ||||
| Б | ||||
| В |
Решение: Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий.
Пусть пропорции выпускаемой продукции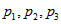 
, 
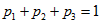. Введем переменные 
, 
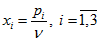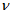‒ гарантированная прибыль.
Для определения оптимальных пропорций выпускаемой продукции составляем следующую задачу линейного программирования:
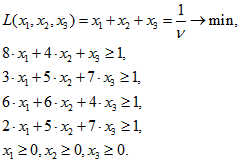
Решение данной задачи симплекс методом процесс трудоемкий, поэтому покажем, как данную задачу можно решить, используя математический пакет Maple.
1. Подключаем пакет simplex:
> with(simplex):
2. Задаем целевую функцию:
> z:=x[1]+x[2]+x[3];
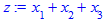
3. Задаем систему ограничений:
> C:=[8*x[1]+4*x[2]+x[3]>=1,3*x[1]+5*x[2]+7*x[3]>=1, 6*x[1]+6*x[2]+4*x[3]>=1, 2*x[1]+5*x[2]+7*x[3]>= 1];
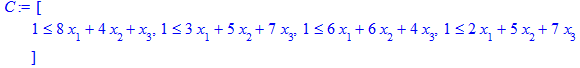
4. Находим минимальное значение:
> X:=minimize(z,C,NONNEGATIVE); evalf(X,5); z[min]:=subs(X,z);
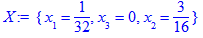
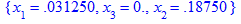
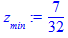
5. Вычисляем цену игры по формуле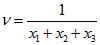 
:
> V:=1/(x[1]+x[2]+x[3]): v:=subs(X,V): v:=v=evalf(v,5);
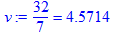
6.Вычисляем пропорции выпускаемой продукции по формулам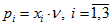 
:
> p[1]:=v*subs(X,x[1]);
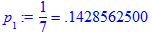
> p[2]:=v*subs(X,x[2]);
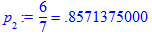
> p[3]:=v*subs(X,x[3]);
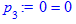
Пример 2. Найти (графически) решение и цену игры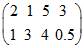 
.
Решение: Необходимо определить оптимальные стратегии
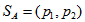и 
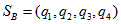. Пусть 
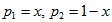частоты применения первым игроком (с горизонтальными стратегиями), соответственно, первой и второй стратегий. Тогда его выигрыш, в зависимости от «чистых» стратегий, применяемых вторым игроком, соответственно составляет:
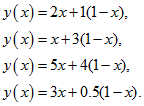
1.Проведем геометрические построения:
> with(plots):inequal({x>=0, x<=1, y<=2*x+(1-x), y<=x+3*(1-x), y<=5*x+4*(1-x), y<=3*x+0.5*(1-x)}, x=0..1,y=0..5);
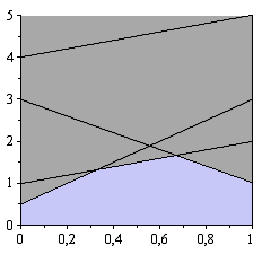
Рис. 1
Ординаты точек ломаной, разделяющей черную и серую области, — минимальный выигрыш первого игрока, в зависимости от применяемой им стратегии. Минимальный выигрыш максимален для точки пересечения первой и второй прямых.
2. Для первого игрока решаем систему уравнений:
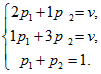
> rez:=solve({v=2*p[1]+p[2],v=p[1]+3*p[2], p[1]+p[2]=1}, {v,p[1],p[2]});
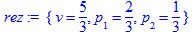
3. Для второго игрока решаем систему уравнений:
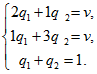
> rez:=solve({v=2*q[1]+q[2], v=q[1]+3*q[2], q[1]+q[2]=1, q[3]=0, q[4]=0}, {v,q[1],q[2],q[3],q[4]});
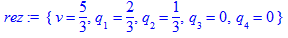
Пример 3. Найти (графически) решение и цену игры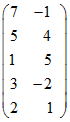 
.
Решение: Необходимо определить оптимальные
стратеги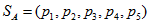и 
и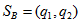 
. Пусть 
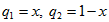частоты применения вторым игроком (с вертикальными стратегиями), соответственно, первой и второй стратегий. Тогда его выигрыш, в зависимости от «чистых» стратегий, применяемых первым игроком, соответственно составляет:
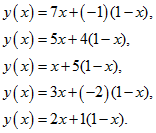
1.Проведем геометрические построения:
>with(plots): inequal({x>=0, y>=7*x+(1-x), y>=5*x+4*(1-x), y>=x+5*(1-x), y>=3*x-2*(1-x), y>=2*x+(1-x),x<=1}, x=0..1, y=-2..7);
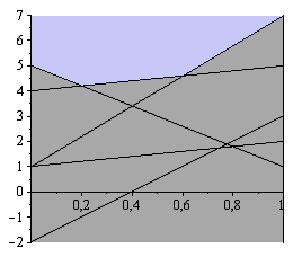
Рис.2.
Ищем минимальную точку на максимальной ломаной. Минимакс равен ординате точки пересечения второй и третьей прямых.
2. Для первого игрока решаем систему уравнений:
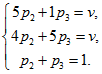
>rez:=solve({v=5*p[2]+p[3], v=4*p[2]+5*p[3], p[1]=0, p[4]=0, p[5]=0, p[2]+p[3]=1}, {v,p[1],p[2],p[3],p[4],p[5]});
3.Для второго игрока решаем систему:
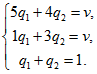
>rez:=solve({v=5*q[1]+4*q[2], v=q[1]+5*q[2], q[1]+q[2]=1}, {v,q[1],q[2]});
