Алгебра логики (законы логики)

Подобно тому, как в алгебре изучают общие свойства числовых выражений, так и в математической логике изучают общие свойства выражений, составленных из высказываний с помощью логических операций. Этот раздел математической логики называют алгеброй логики.

В обычной алгебре числа заменяют буквами и когда формулируют какой-либо закон, например a(b+c)=ab+ac, то подразумевают, что он выполняется на некотором множестве числовые значений тех переменных, которые в него входят. В алгебре логики тоже используют буквы не только для обозначения конкретных высказываний, но и для обозначения логических переменных. Только эти переменные могут принимать лишь два значения И и Л (истина и ложь). Логические выражения, полученные из этих переменных с помощью логических операций, также могут принимать лишь два значения И и Л. Пользуясь таблицами истинности операций, можно составить таблицы истинности и различных выражений. При этом законы логики (так же, как и законы алгебры) позволяют упрощать многие выкладки и рассуждения.

Мы не будем изучать эти законы и даже формулировать их (подумайте, сколько времени Вы изучаете обычную алгебру?). Мы только рассмотрим некоторые примеры и решим задачи.

Пример1. Составить таблицу истинности выражения .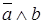

Решение. Выпишем в таблице все возможные сочетания значений а и b и воспользуемся таблицами истинности отрицания и конъюнкции. Получим

а	b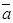
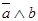
и	и	л	л
и	л	л	л
л	и	и	и
л	л	и	л

Пример 2. Составить таблицу истинности выражений .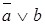

Решение. Так же, как и в примере 1, выпишем в таблице все возможные значения а и b и используем таблицы истинности логических операций отрицания и дизъюнкции. Будем иметь

а	b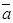
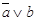
и	и	л	и
и	л	л	л
л	и	и	и
л	л	и	и

Может случиться, что для двух внешне различных логических выражений таблицы истинности одинаковы. Такие логические выражения принято называть равносильными и писать а↔b.

Если сравнить только что полученную таблицу истинности 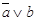с таблицей истинности а→b, то мы увидим, что они одинаковые. Значит, 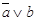↔ а→b. (В обычной алгебре такие выражения называют равными),

С помощью таблицы истинности легко проверить и такую равносильность: 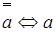(закон двойного отрицания)/ В самом деле, таблица истинности имеет вид:

а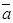
И	Л	И
Л	И	Л

Пример 3. Доказать, что .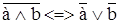

Решение. Составим таблицы истинности для выражений, стоящих в левой и правой частях первой формулы (их удобна совместить). Получим

a	b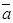
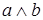
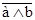
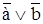
И	И	Л	Л	И	Л	Л
И	Л	Л	И	Л	И	И
Л	И	И	Л	Л	И	И
Л	Л	И	И	Л	И	И

Сравнивая два последних столбца, мы видим, что они одинаковые. Значит, утверждение доказано.

Задача. На вопрос, кто из трех учащихся изучал логику, был получен правильный ответ- если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй. Кто из учащихся изучал логику?

Решение. Обозначим через а,b,с высказывания, состоящие соответственно в том, что первый, второй, третий учащиеся изучали логику. Запишем условие задачи с помощью а,b,с и логических операций. Получим выражение

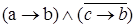
Известно, что это высказывание истинно. Если бы мы знали алгебру логики, то занялись упрощением этого выражения. Составить таблицу истинности полученного выражения. Она имеет вид:

а	b	с
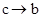
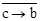
И	И	И	И	И	Л	Л
И	И	Л	И	И	Л	Л
И	Л	И	Л	Л	И	Л
И	Л	Л	Л	И	Л	Л
Л	И	И	И	И	П	Л
Л	И	Л	И	И	Л	Л
Л	Л	И	И	Л	И	И
Л	Л	Л	И	И	Л	Л

Только в предпоследней строке получившееся выражение принимает значение И, а все остальные значения Л. При этом высказывания а и b -ложны, а с - истинно. Значит, логику изучал только третий учащийся.