АЛГОРИТМЫ ФИЛЬТРАЦИИ СИГНАЛОВ В АСУТП

ЛАБОРАТОРНАЯ РАБОТА № 5.1

Цель. Ознакомление с наиболее распространенными в АСУТП алгоритмами фильтрации измеряемых случайных сигналов, проведение сравнительного анализа их точности и особенностей реализации в ЦВМ.

Задание. 1) составить и отладить подпрограммы фильтрации для ЦВМ по методам скользящего среднего, экспоненциального сглаживания и статистической фильтрации по одной точке замера, 2) для заданных характеристик случайных сигналов рассчитать оптимальные параметры фильтров, 3) смоделировать систему фильтрации на ЦВМ и вычислить погрешность фильтрацию по каждому из рассмотренных методов, 4) провести сравнительный анализ эффективности рассмотренных алгоритмов.

Основные положения. 1 Постановка задачи оптимальной фильтрации. Сигналы от измерительных устройств часто содержат случайную погрешность – помеху. Задача фильтрации состоит в том, чтобы в той или иной степени отделить полезную составляющую сигнала от помехи. Как правило, и полезный сигнал, и помеха предполагаются стационарными случайных процессами для которых известны их статистические характеристики: математическое ожидание, дисперсия, корреляционная функция, спектральная плотность. Зная эти характеристики нужно найти фильтр в классе линейных динамических систем или в более узком классе линейных систем с заданной структурой так, чтобы сигнал на выходе фильтра возможно меньше отличался от полезного сигнала.

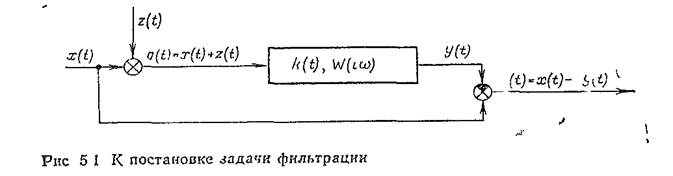
Введем обозначения и поставим задачу фильтрации точнее. Пусть на вход фильтра с импульсной характеристикой к(t) и соответствующей (в силу Фурье преобразования) 0

АФХ W(iω) поступают полезные сигналы x(t) и некорреляционная с ним помеха z(t) (рис.5.1). Корреляционные функции и спектральные плотности полезного сигнала и помехи обозначим R_x(t), S_x(t), R_z(t) и S_z(t). Требуется найти характеристики фильтра k(t) или W(t) так, чтобы среднеквадратичное значение разности ε между сигналом на выходе фильтра и полезным сигналом x было минимальным. Если характеристика фильтра известна с точностью до одного или нескольких параметров, то надо выбрать оптимальные значения этих параметров.

Ошибка ε содержит две составляющие. Первая (ε₁) связана с тем, что некоторая часть помехи все же пройдет через фильтр, а вторая (ε₂) – с тем, что форма полезного сигнала при прохождении через фильтр изменится. Таким образом, определение оптимальной характеристики фильтра представляет собой поиск компромиссного решения, минимизирующего суммарную погрешность.

Представим частотную характеристику фильтра в виде:

W(iω) = A(ω)exp[if(ω)].

По формулам, связывающим спектральные плотности случайных процессов на входе и выходе линейной системы с ее частотной характеристикой подсчитываем спектральные плотности каждой из составляющих ошибки.

Для ошибки, связанной с пропуском помехи, получим

S_ε1(ω) = S_z(ω)A²(ω)

Спектральная плотность ошибки, связанной с искажением полезного сигнала, равна

S_ε2(ω) = S_x(ω)|1 – W(iω)|²

Сумма этих составляющих S_ε имеет спектральную плотность

S_ε(ω) = S_ε1(ω) + S_ε2(ω)

Если учесть, что

|1 – W(iω)|² = [1 – А(ω)cosf(ω)]² + А²(ω) sin²f(ω),

получим

S_ε(ω) = S_z(ω)A²(ω) + S_x(ω)A²(ω) + S_x(ω) – 2S_x(ω)A(ω)cosf(ω). (5.1)

Среднеквадратичная ошибка связана со спектральной плотностью выражением

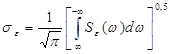
Минимизируя S_ε(ω) по f(ω) и А(ω), приходим к уравнениям

cos f*(ω) = 1 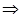f*(ω) = 0

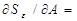2S_z(ω)A(ω) – 2S_x(ω)[1 – A(ω)] = 0

или

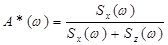(5.2)

Найденным характеристикам оптимального фильтра соответствует спектральная плотность ошибки

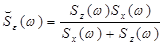
Минимальная среднеквадратичная ошибка

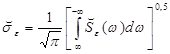(5.3)

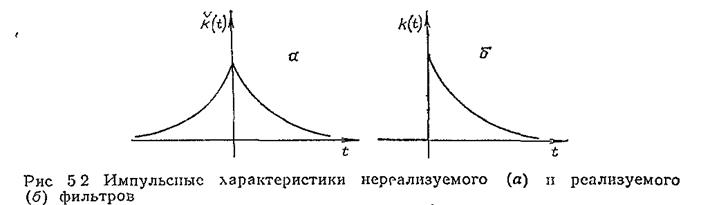
К сожалению, найденный фильтр не реализуем так как условие равенства нулю на всех частотах фазо-частотной характеристики означает, что импульсная характеристика фильтра – четная функция она отлична от нуля не только при t>0, но и при t<0 (рис 5.2,а)/

Для любого физически реализуемого фильтра справедливо требование: к(t) = 0 при t<0 (рис 5.2,б). Это требование следовало бы ввести в постановку задачи. Естественно, что достижимая ошибка σ при этом возросла бы. Задача оптимальной фильтрации с учетом физической реализуемости была решена.

 

Н. Винером (см., например, [11]). Ее решение значительно сложнее приведенного выше, поэтому в данной работе будем искать физически реализуемые фильтры лишь в классе фильтров, характеристики которых заданы с точностью до значений параметров. Величина же , рассчитанная по формуле (5.3), может служить нижней оценкой достижимой погрешности фильтрации.

Физический смысл соотношения (5.2,б) иллюстрируется рис. 5.3. Если спектры полезного сигнала и помехи не перекрываются, то А(ω) должно быть равно нулю там, где спектральная плотность помехи отлична от нуля, и равно единице для всех частот, на которых S_x(ω)>0. На рис. 5.3,6 показан, характер А*(ω) в случае, когда спектральные плотности сигнала и помехи перекрывают друг друга.

Среди фильтров с заданной структурой наиболее широкое распространение нашли фильтры, основанные на операции скользящего среднего, а также экспоненциальный фильтр и так называемый статистический фильтр нулевого порядка. Экспоненциальный фильтр представляет собой апериодическое звено первого порядка, а статистический фильтр нулевого порядка – усилительное звено. Рассмотрим каждый из упомянутых фильтров подробнее.

Фильтр скользящего среднего. Выход фильтра связан с его входом соотношением

Импульсная переходная функция фильтра показана на рис. 5.4,а. Частотные характеристики равны

Импульсная характеристика может быть выражена через функцию Хевисайда 1(t)

k(t) = k[1(t) – 1(t – T)].

Настраиваемыми параметрами фильтра являются коэффициент усиления k и память Т.

Экспоненциальный фильтр (рис. 5.4,б). Сигнал на выходе определяется дифференциальным уравнением

y/γ + y = kg

Импульсная характеристика имеет вид:

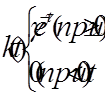
Частотные характеристики

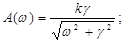
Параметрами фильтра являются коэффициент усиления k и постоянная времени, обратная величине γ.

Статистический фильтр нулевого порядка. Этот фильтр, как упоминалось выше, является усилительным звеном. Его характеристики

y(t) = kg(t); A(ω) = k; f(ω) = 0

Вес перечисленные фильтры не позволяют добиться идеальной фильтрации даже при непересекающихся спектрах сигнала и помехи. Минимизировать ошибку σ_ε можно, подбирая параметры k, Т, γ. При этом нужно характеристики фильтра А(ω) и f(ω) как функции частоты и параметров подставить в формулу (5.1), взять интеграл от получившегося выражения, который будет функцией параметров фильтра, и найти минимум этого интеграла по параметрам.

Например, для статистического фильтра кулевого порядка спектральная плотность ошибки будет иметь вид:

S_ε(ω) = S_z(ω)k² + S_xω(1 – k²)

Интеграл S_ε равен дисперсии помехи, умноженной на π. Получим

Учтем, что интегралы в правой части этого равенства равны дисперсиям полезного сигнала, и помехи, так что

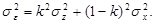
Условие минимума этого выражения по k приводит к равенству

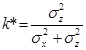
После подстановки найденного значения k в выражение для дисперсии ошибки получим:

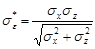
Фильтры текущего среднего и экспоненциальный имеют по два настраиваемых, параметра, и их оптимальные значения не

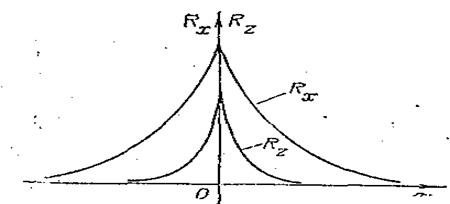
Рис. 5.6. Автокорреляционные функции полезного сигнала Rx(τ) и шума Rz(τ).

удастся так легко выразить через характеристики полезного сигнала и помехи, однако эти значения можно найти численными методами поиска минимума функции по двум переменным.

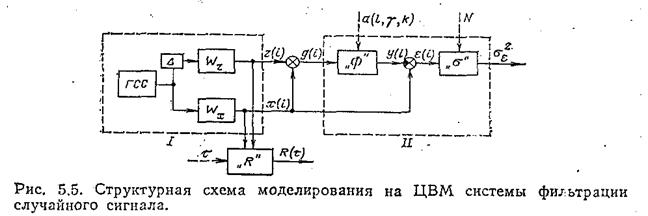
2. Описание моделируемой системы. Работа проводится путем моделирования на ЦВМ системы, состоящей из следующих блоков (рис. 5.5).

1. Генератор входного сигнала I, включающий генератор случайного сигнала (ГСС) и два формирующих фильтра с заданными характеристиками W_x(iω) и W_z(iω), на выходе которых получают полезный сигнал x(t) и помеху z(t). Между генератором случайного сигнала и формирующим фильтром W_z включено звено запаздывания Δ, обеспечивающее сдвиг на два-три такта. При этом вход фильтра, формирующего помехи, и вход фильтра, формирующего полезный сигнал, оказываются некоррелированными друг с другом.

2. Блок расчета корреляционных функций .

3. Блок фильтрации (II), включающий собственно фильтр и блок расчета погрешности фильтрации .

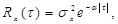
Генерируемые в системе полезный сигнал x(t) и помеха z(t) являются стационарными случайными процессами, корреляционные функции которых могут быть приближенно аппроксимированы экспонентами вида (рис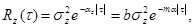. 5.6)

(5.6)

где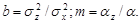

Оценки дисперсий сигналов 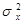и рассчитывают с помощью блока 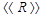(при τ = 0); параметры α и α_z задаются преподавателем.

3. Дискретная реализация непрерывных фильтров. В работе используют дискретные реализации описанных выше непрерывных фильтров. Шаг дискретности t_o принимают существенно меньше, чем время затухания корреляционных функций полезного сигнала и шума. Поэтому записанные выше выражения (5.1) для подсчета σ_ε через спектральные характеристики входного сигнала и шума могут быть использованы и в дискретном случае.

Найдем сначала дискретные аналоги фильтров, формирующих из сигнала, получаемого от ГСС, случайные процессы с корреляционными функциями (5.6). Спектральные плотности, соответствующие этим корреляционным функциям, имеют вид

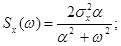
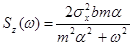(5.7)

Передаточные функции формирующих фильтров для случая, когда дисперсия сигнала на выходе ГСС равна единице, равны

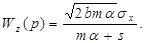
Нетрудно видеть, что

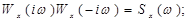
Если сигнал на входе каждого из формирующих фильтров обозначить через ξ, то дифференциальные уравнения, соответствующие передаточным функциям, записанным выше, имеют вид

Соответствующие им разностные аналоги запишутся в виде;

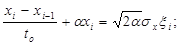
Таким образом, алгоритм работы фильтра, формирующего, полезный сигнал, имеет вид:

(5.8a)

Аналогично для фильтра, формирующего помехи

(5.8б)

Аналоги непрерывных фильтров, предназначенных для выделения помехи, имеют следующий вид:

для фильтра скользящего среднего

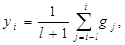(5.9)

где величину l выбирают из условия (l + 1)t_о = T;

для экспоненциального фильтра

(5.10)

для статистического фильтра нулевого порядка

у_i = kg_i (5.11)

Порядок выполнения. 1. Составить и отладить подпрограммы блока фильтрации текущей информации и вычисления погрешностей фильтрации.

2. Получить реализации случайных процессов на выходе формирующих фильтров и по ним найти оценки дисперсий полезного сигнала и помех, а также корреляционных функций R_x(τ) и R_z(τ). Приближенно определить α_х и α_z и сравнить с расчетными.

3. Рассчитать по S_x(ω) и S_z(ω) аналитически или на ЦВМ нижнюю оценку для среднеквадратичной ошибки фильтрации.

4. По формуле (5.4) найти оптимальный коэффициент усиления статистического фильтра нулевого порядка и соответствующее ему значение , которое сравнивается с .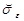

5. Использую один из известных методов поиска минимума функции двух переменных и составленную заранее программу, найти оптимальные параметры скользящего среднего и экспоненциального фильтров и среднеквадратичные ошибки фильтрации. При этом конкретному сочетанию параметров фильтра соответствует спектральная плотность ошибки S_ε(ω), определяемая формулой (5.1), а по ней находят значение 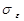после численного интегрирования.

6. Ввести в ЦВМ программы фильтрации, определить экспериментально среднеквадратичную ошибку для оптимальных и отличных от оптимальных параметров фильтров, сравнить результаты с расчетными.

7. Провести сравнительный анализ эффективности различных алгоритмов фильтрации по следующим показателям: а) минимально достижимая среднеквадратичная ошибка.; б) требуемый объем оперативной памяти; в) время счета на ЦВМ.

Отчет должен содержать: 41) структурную схему системы (см. рис. 5.5); 2) подпрограммы формирующих и синтезируемых фильтров;. 3) расчет оптимальных параметров фильтров и соответствующих им значений среднеквадратичной погрешности; 4) результаты анализа рассмотренных алгоритмов и выводы.