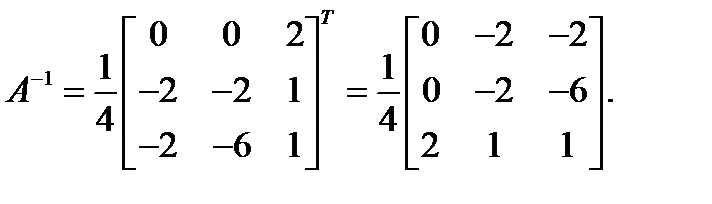Лекция 3
1. Вычисление определителей
Некоторые важные свойства определителей:
Утверждение 1. (без доказательства)
det(AB)=det A 
det B.
Утверждение 2. (без доказательства)
det E =1.
Утверждение 3. (без доказательства)
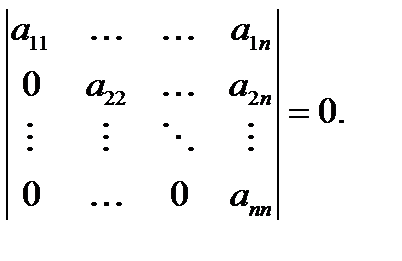
Определитель треугольной матрицы равен произведению диагональных элементов:
1. Миноры и алгебраические дополнения. Вычисление определителя разложением по строке и столбцу. Определитель Вандермонда
Определение 1. Минором k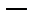 
того порядка матрицы А называется определитель матрицы, получаемой при пересечении некоторых k строк и k столбцов матрицы А.
Можно сформулировать определение минора для квадратной матрицы немного иначе: минором k 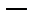ого порядка называется определитель матрицы, получаемой после вычеркивания некоторых (n-k) строк и (n-k) столбцов исходной матрицы А.
Определение 2. Минором элемента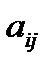 
называется минор (n-1) го порядка, получаемый вычерчиванием i той строки и j того столбца.
Определение 3. Алгебраическим дополнением элемента 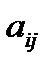называется величина 
:
.
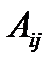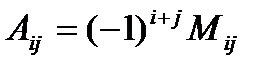Пример. 
, 
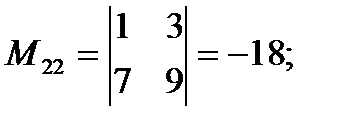
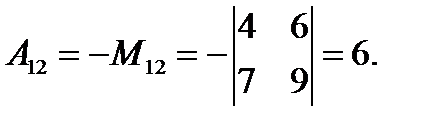
Лемма (без доказательства). Величина 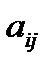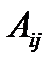представляет собой сумму (n-1)! произведений элементов матрицы А, взятых с теми же знаками, с которыми они входят в определитель det A.
Теорема (о вычислении определителя разложением по i -той строке).
(*)
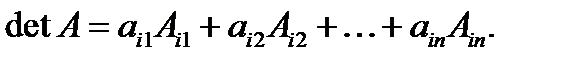Замечание. Правая часть равенства (*) называется разложением определителя по i 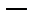той строке.
Доказательство теоремы. Правая часть формулы (*) представляет собой сумму n(n-1)!=n! произведений различных элементов матрицы А, причем, в силу леммы, они входят с тем же знаком, с каким они входят в определитель det A.
Правая часть равенства (*) не может содержать одинаковых слагаемых, так как, например, все слагаемые, содержащие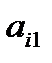 
, могут содержаться только в группе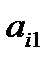 
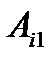. Внутри группы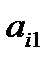 
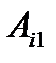тоже не может быть повторов. Следовательно, левая и правая части равенства (*) состоят из одних и тех же слагаемых без пропусков и повторений. Отсюда получаем справедливость равенства (*):
|
|
. ▲
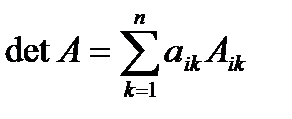Следствие. Так как определитель матрицы не меняется при её транспонировании, то можно выписать форму разложения определителя по j 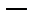тому столбцу:
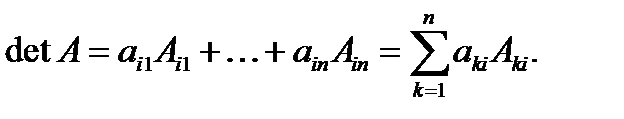
Замечание (об определителе Вандермонда). В приложениях часто используется определитель Вандермонда:
Пример.
n =3: 
Замечание. На практике, прежде чем вычислить определитель матрицы большого порядка, обычно преобразуют матрицу к треугольному виду, используя метод Гаусса (этот метод будет изложен немного позднее).
2. Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Вырожденная матрица
Пусть А 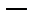квадратная матрица порядка 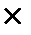n 
n.
Определение 1. Матрица В (С) называется левой (правой) обратной к матрице А, если ВА = Е (АС=Е).
Утверждение 1. Пусть левая и правая обратная матрицы существуют. Тогда эти матрицы совпадают: В=С.
Доказательство. Пусть ВА=Е, АС=Е. Имеем: В=ВЕ=В (АС)=(ВА) С = ЕС=С.
▲
Определение 2. Матрица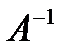 
= В=С (где В и С – левая и правая обратные матрицы) называется обратной матрицей к матрице А.
Можно сформулировать определение обратной матрицы иначе:
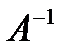- обратная к А, если А 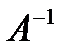= 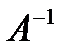А = Е.
Определение 3. Матрица А называется невырожденной, если det A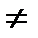 
0
Лемма (о фальшивом разложении определителя).
(*)
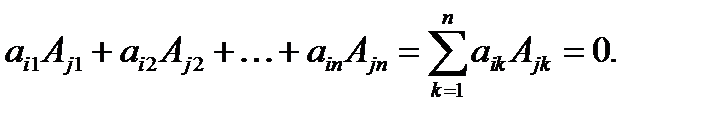Доказательство. В левой части равенства (*) выписано разложение по j 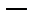той строке определителя матрицы, i 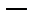тая и j 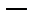тая строки которой совпадают. Определитель такой матрицы равен 0.
▲
|
|
Теорема (о существовании обратной матрицы).
Обратная матрица к матрице А существует тогда и только тогда, когда матрица А является невырожденной.
Доказательство. 1. Необходимость.
Пусть существует обратная матрица: А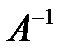 
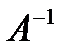= А = Е. Возьмем определитель от обоих частей равенства, используем тот факт, что определитель произведения матрицы равен произведению определителей:
det(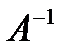) det A =det E =1.
Следовательно, det A 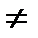0.
2.Достаточность.
Пусть det A 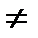0. Докажем, что матрица В, определяемая равенством
В =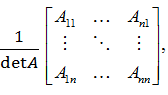 
является обратной к матрице А (здесь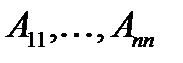 
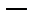алгебраические дополнения к соответствующим элементам матрицы А).
Рассмотрим произведение ВА:
ВА =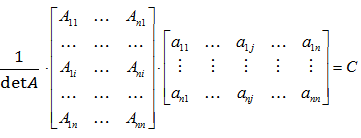 
,
где
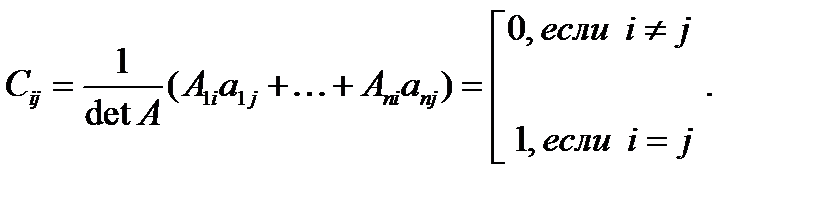
Отсюда С=Е, т.е. матрица В является левой обратной к матрице А. Аналогично доказывается, что матрица В является правой обратной к матрице А: АВ=Е. Отсюда получаем, что выполнено В = .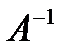
▲
Замечание. Доказана формула
= 
= 
= 
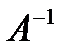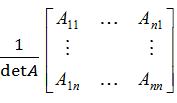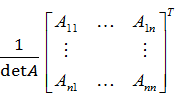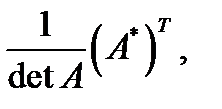
где 
- так называемая союзная матрица.
Утверждение.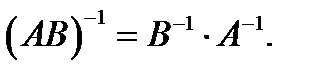 
Доказательство.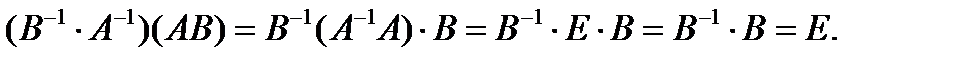 
Аналогично доказывается, что
▲
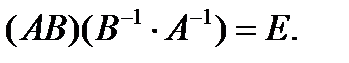
Пример. Вычислим обратную матрицу для матрицы А:
Решение.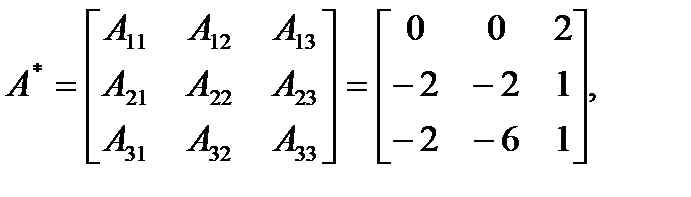 
det A =4; 