Лабораторная работа №1
Эта лабораторная работа посвящена моделированию к онечных а втоматов(КА) и р егулярных в ыражений(РВ) в среде FSP-LTS
Зачёт ставится при условии решения по каждому из двух предлагаемых вопросов любых трёх задач (по выбору преподавателя) «сходу» и только на «чистом» листе и
ответа на теоретические вопросы
Пожелание. По возможности сделайте решение в среде FSP-LTS
Задания лабораторной работы
Вопрос 1
Имеется алфавит å = { a, b }.
Для каждого перечисленного ниже пункта постройте граф КА.
1) String of even length.
2) String of odd length.
3) String with an odd number of a 's.
4) String not containing ba as asubstring.
5) String not ending with aab.
6) Цепочка не оканчивается подстрокой ababa
7) Цепочка не может закончится подстрокой aaab
8) String ending with neither ab nor aabb.
9) String containing abab as a substring.
10) String that contain aba as a substring.
11) String containing both ab and ba as substring.
12) String containing neither aa nor bb as substring.
13) Цепочка не может содержать ни подстроку abb ни подстроку baa
14) String in which the thirdletter from the right is b.
15) String with at most one occurrence of aa and one occurrence of bb.
16) String that end in ab.
Пример решения(файл FSaa.lts) в среде FSP-LTS
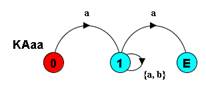// Для алфавита {а,b}. Строка начинается и кончается на "а"
KAaa = (a -> KA2),
KA2= ({b,a}-> KA2
| a-> END).
Вопрос 2
Имеется алфавит å = {x,y}.
Надо написать РВ для получения следующих цепочек из заданного алфавита.
1) String that begin with x and end with y.
2) String that contain at least two x’ s.
3) String that contain at least one x and at least one y.
4) String that have length at least 2 and whose last but one symbol is x.
5) String which contain the substring yy.
6) String whose length is at least 3.
7) String that start with x and have odd length.
8) String for which every letter at an even position is x.
9) String that contain at least two x’ s and at most one y.
10) String that aren’t equal to yy or yyy.
11) String that contain an even number of x.
12) String that do not contain the string xy.
13) String that do not contain the string yxy.
|
|
14) Цепочка содержит подстроку yx и притом только один раз.
15) Цепочка не должна начинаться с xy.
16) Цепочка должна обязательно содержать xxx, но ровно один раз.
Примеры решения (в среде FSP-LTS) можно найти в файле RegExpr.lts
// Символ подчёркивания «_» обозначает пустой символ.
// Для алфавита {а,b}. Регулярные выражения
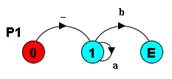// P1 = a*b ------------------------
P1 = (_-> P01),
P01= (b-> END
| a-> P01).
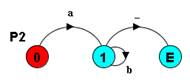// P2 = ab* ------------------------
P2 = (a-> P03),
P03 =(_-> END
| b-> P03).
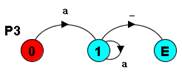// P3 = aa* ------------------------
P3 = (a-> P03),
P03 =(a-> P03
| _-> END).
// P4 = (a b c)* -----------------
P4 = (_-> END
| a-> b-> c-> P4).
// P5 = ((a|b)(cd)*)* -------------
// Число состояний = 6...
P5 = ({a,b}-> P05
| _-> END),
P05 = ({a,b}-> P05
| _-> END
| c-> d-> P15),
P15= ({a,b}-> P05
| _-> END
| c-> d-> P15).
// Минимальное число состояний = 4
P5min = (_ -> END
| {a, b} -> P5min1),
P5min1 = (_ -> END
| {a, b} -> P5min1
| c -> d -> P5min1).
// P6 = (a | b)* a b b -------------
P6 = ({a, b}-> P06
| {a, b}-> P16),
P06 = ({a, b}-> P06
| {a, b}-> P6),
P16 = (a -> b -> b -> accept -> END).
Дополнительные (теоретические) вопросы.
1. Конечный автомат (КА). Определение. Примеры.
2. Детерминированный конечный автомат (ДКА). Определение. Примеры.
3. Недетерминированный конечный автомат (НКА). Определение. Примеры.
4. Конечный автомат Büchi(КАБ). Определение. Примеры.
5. Регулярные выражения (РВ). Определение. Примеры.