Пересечение множеств
Рассмотрим два множества: Х = {0, 1, 3, 5}, Y = {1, 2, 3, 4}.
Числа 1 и 3 и только они принадлежат одновременно обоим множествам Х и Y. Составленное из них множество {1, 3} содержит все общие для множеств Х и Y элементы.
Множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В, называется пересечением множеств А и В, и обозначается А ∩ В. А ∩ В = {х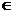 
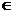А и х В}.
Таким образом, множество {1, 3} является пересечением рассмотренных множеств Х и Y: {0, 1, 3, 5} ∩ {1, 2, 3, 4} = {1, 3}.
В том случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А ∩ В = Ø.
Пересечение любого множества А с пустым множеством есть пустое множество: А ∩ Ø = Ø.
Алгебраические операции над множествами и их свойства излагаются обычно с применением кругов Эйлера или диаграмм Венна (или диаграмм Эйлера-Венна).
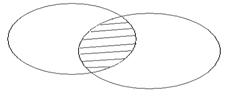
Пересечением множеств А и В, у которых есть общие элементы, будет заштрихованная область.
А ∩ В
Если множества не имеют общих элементов, то их пересечение будет выглядеть так:
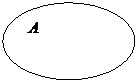
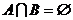
Если одно из множеств является подмножеством другого, то их пересечение будет выглядеть так:
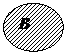
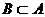
Объединение множеств
Вновь возьмём множества Х = {0, 1, 3, 5} и Y = {1, 2, 3, 4} и наряду с ними рассмотрим множество {0, 1, 2, 3, 4, 5}. Это множество содержит все элементы множества Х и все элементы множества Y и не содержит никаких других элементов.
Множество, состоящее из всех элементов, принадлежащих или множеству А или множеству В, называется объединением множеств А и В, обозначается А U В. А U В = { х 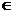А или х 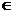В }
Итак, {0, 1, 3, 5}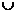 
{1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.
Если изобразить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью.
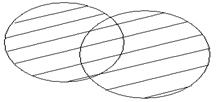
А U В
Если множества не имеют общих элементов, то их объединение выглядит так:
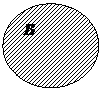
А U В
Если одно из множеств является подмножеством другого, то их объединение будет выглядеть так:
 |
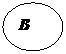А U В
Часто приходится рассматривать объединение и пересечение трёх и более множеств. Объединение множеств А, В и С есть множество, каждый элемент которого принадлежит хотя бы одному из множеств А, В или С; пересечение множеств А, В и С есть множество всех элементов, принадлежащих и множеству А, и множеству В, и множеству С.
А U В U С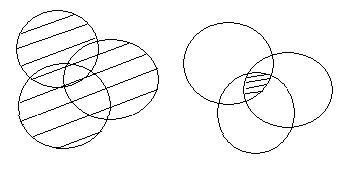 
А ∩ В ∩ С
Например, объединение множеств остроугольных, тупоугольных и прямоугольных треугольников есть множество всех треугольников.
Еще операции над множествами можно показать с помощью детского анекдота: Однажды лев, царь зверей, собрал зверей на поляне и повелел им разделиться на умных и красивых. После того, как пыль улеглась, лев увидел на поляне две большие группы зверей и мартышку, прыгающую между ними. На вопрос: почему она прыгает туда, сюда, мартышка ответила: «Что мне, разорваться, что ли?». Так вот, мартышка из анекдота – это пример пересечения умных зверей и красивых. А объединением умных и красивых зверей является все множество зверей.
Объединение и пересечение множеств обладают многими свойствами, аналогичными свойствам суммы и произведения чисел:
| № п/п | Свойство операций над множествами | Свойство арифметических операций | Название свойства |
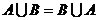
| a + b = b + a | Коммутативность | |
| 
| ||
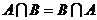
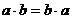
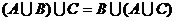
| (а+b)+c = a+(b+c) | Ассоциативность | |
| 
| ||
| 
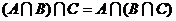
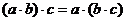
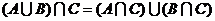
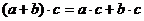
| Дистрибутивность |
Однако эта аналогия не всегда имеет место. Например, для множеств справедливы равенства:
6. (А U С) ∩ (В U С) = (A ∩ B) U С.
7. А U А = А.
8. А ∩ А = А.
Соответствующие равенства для чисел верны не всегда.
Заметим, что, если в выражении есть знаки пересечения и объединения множеств, и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.
Вычитание множеств
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.
Разностью множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В, обозначается А \ В. А \ В = { х 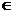А и х 
В }.
Х \ Y = {0, 1, 3, 5} \ {1, 2, 3, 4} = {0, 5}. Если мы найдем разность множеств Y и Х, то результат будет выглядеть так: Y \ X = {2; 4}. Таким образом, разность множеств не обладает переместительным (коммутативным) свойством.
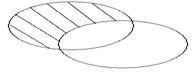Если изобразить множества А и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью.
А \ В
Если множества не имеют общих элементов, то их разность будет изображаться так:
 |
 |
А \ В
Если одно из множеств является подмножеством другого, то их разность будет изображаться так:
А \ В
Пересечение – более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении А \ В ∩ С такой: сначала находят пересечение множеств В и С, а затем полученное множество вычитают из множества А. Что касается объединения и вычитания множеств, то их считают равноправными. Например, в выражении А \ В U С надо сначала выполнить вычитание (из А вычесть В), а затем полученное множество объединить с множеством С.
Вычитание множеств обладает рядом свойств:
1. (А \ В) \ С = (А \ С) \ В.
2. (А U В) \ С = (А \ С) U (В \ С).
3. (А \ В) ∩ С = (А ∩ С) \ (В ∩С).
4. А \ (В U С) = (А \ В) ∩ (А \ С).
5. А \ (В ∩ С) = (А \ В) U (А \ С).
Дополнение
В случаях, когда одно из множеств является подмножеством другого, А \ В называют дополнением множества В до множества А, и обозначают символом В'А
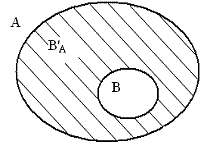
Пусть В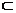 
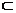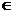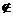А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В. В А, А \ В = В ' А, В ' А = { х | х А и х В }.
Часто ограничиваются рассмотрением всевозможных подмножеств одного и того же множества, которое в этом случае называют основным или универсальным множеством. Обозначим основное множество буквой E. Для любого множества А, принадлежащего основному множеству Е, справедливы равенства: А U Е = Е, А ∩ Е = А.
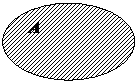
Множество элементов основного множества Е, не принадлежащих множеству А, называется дополнением множества А до множества Е или просто дополнением и обозначается А'.
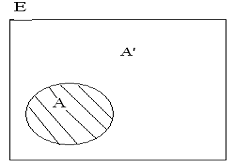Объединение множества А и его дополнения А' есть основное множество: А U А' = E.
Пересечение множества со своим дополнением пусто: А ∩ А ' = Ø.
Дополнение пустого множества есть основное множество: Ø' = E, а дополнение основного множества пусто: Е' = Ø.
На рисунке основное множество Е схематически изображено в виде прямоугольника, его подмножество А заштриховано, не заштриховано дополнение множества А'.
Формула Грассмана.
Теория множеств используется при решении задач следующего вида: