Количество функций определяется по формуле 
Эти функции носят название элелинтарных
| Х1 | Х2 | Fx | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
| Название условное обозначение | Никогда f=0 | «Н» ^& коньюнция | «нет запрет | То же f3-X1 | Запрет по Х1 | Повтор f5=X2 | Альтернатива + | «или» V дизьюнкция | «или не» стр ПИРСА | равнозначность | «не» f12=  =X2
| «Если…, то импликация | «не» F12= 
| «если…, то импликация | «И – не» | Всегда F15=1 |
1) 
0 const «0»
2) 
X1^X2 = X1*X2 
логическое умножение
3) 
= Х1=Х2=Х1* 
запрет по Х2
4) 
повторение по Х1
5) 
=X1=X2= *X2 
запрет по Х1
6) 
7) 
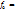X1⊕X2 = X1 
V 
*Х2= неоднозначность сумма по модулю 2
8) 
= X1 V Х2 – дизьюнкция (логическое сложение или)
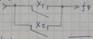
9) 
X1↓Х2 = 
Стрелка Пирса (ИЛИ НЕ)
10) 
= Х1≡Х2 = Х1*Х2 V 
(тождество (равнозначность)
11) 
отрицание по Х2
12) 
= Х1←Х2 = Х1 V 
импликация по Х2
13) 
отрицание по Х1
14) 
= Х1 → Х2 = 
V Х2 импликация по Х1 
15) 
Х1⟂Х2 = 
= V Гитрих Шеффера (И-НЕ)
16) 
=1 const «1»
= 1;
Умножение: x·0 = 0; x· 1 = x; x·x· … ·x = x; x· 
·x2 = x1+x2;
= 
;
= 
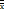= x.
Для решения задач полезны также законы, вытекающие из выражений:
x1+x1 x2 + x1 x3 + x1 x4+ … + x1 xn = x1;
x1+ 
= 
;
= 
= x1;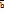 
= x2, имеем: a+ 
b =a+b; 
= ab.Доказательство основных законов алгебры логики производится построением таблиц истинности для обеих частей равенства или другими способами /1...6/.
, где V – в сумму входят только те наборы, где ф-я = 1.
Записать в ДСНФ ф-ю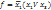 
K=n=3
3 единичных набора. 
;
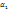
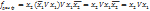
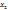
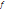
суммируются только коньюнкции, для которых значение функции =0
Проиньертируем обе части
т.к. 
, получим
- КСНФ
Алгоритм перехода
1. Определяется по таблице истинности те наборы входных переменных, на которых знач. Функции = 0
2. Записывается дизьюнкции для каждого аргументов по правилу, если знач. Переменных = 0, то берется переменное значение, если значение переменной =1, то берется инверсное значение
3. Вес дизьюнкции аргументов соединяются знаками коньюнкций (логического умножения)
Например: по таблице истинности записать функцию в виде КСНФ
)*( 
=Х1Х2 V Х1Х3
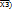V Х1Х3 (Х2 V 
=
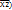V X1 
Дезьюнкцией нормальной формой ДНФ называется такая форма записи ФАЛ, когда функция представляет собой сумму произведенной входных переменны, но в отличие от ДСНФ в произведении некоторые переменные могут отсутствовать.
Теорема 6: любую ФАЛ от n переменных можно представить в виде:
f(X1 
Доказательство: Х1=1, 
f(1.0; Xn 
Следствии 1
X1+f (X1 
Следствие 2
X1+f (X1 
Вывод: Если параллельной схеме включен контакт Х1, то все одноименные контакты можно оборвать, а инверсные - закоротить
Например:
(X2 V X3 V X1) * (X2 V X3 V 
т.е. число клеток будет равным 1,2,4,8,16
3. Объединение чисел начинать с тех, которые могут войти в единственный контур.
4. В контур можно объединить только соседние клетки, содержащие единицы (нули).
5. Каждой единичной клетке соответствует коньюнкция входных переменных, определяющих данную клетку. Каждой нулевой клетке – дизьюнкция инверсии входных переменных
6. Выражение может быть записано в ДНФ и КНФ
ДНФ – дизьюнкция коньюнкций, соответствует единичным контурам
КНФ – коньюнкция дизьюнкций, соответствует нулевые контуры.
7. При переходе границы переменных между прямым и инверсным значением в контуре, она исключается из выражения контура, которое представляется всеми остальными переменными.
8. Самое простое логическое выражение получается при наибольшем объединение контуров
=
(c V d)* ( 
Метод наиболее эффективен при линейных значений функции 4х переменных, менее эффективен для 3х переменных т.к. они проще упрощаются по законам алгебры логики.
Функция выражение через 
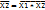
Х1*Х2 
* 
Х1↔Х2 
Х1⊕Х2 
1. Операция с const
Х⟂1 =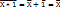 
Х⟂0 = 
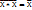Х⟂Х = 
Х⟂Х = 
Гитрих Гиеффера
2. Связь с коньюнкцией
Х1*Х2=Х1*Х2+Х1*Х2 = 
=
= 
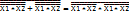= (Х1⟂Х2) ⟂1
В общем случае Х1*Х2… Xn = (Х1⟂Х2⟂…⟂Хn) ⟂1
3. Связь с дизьюнкцией
Х1+Х2 = (Х1 V 1) V (X2 V 1)
В общем случае Х1+Х2+… Xn = (X1 V 1) V (X2 V 1) V … (Xn V 1)
4. Формулы упрощения
1) Х1⟂(Х1⟂Х2) = 
+ 
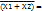
Чтобы перевести любую ФАЛ в базис И-НЕ необходимо выполнить:
1) Представить функцию в ДНФ
2) Все знаки сложения и умножения заменить на знак И-НЕ (⟂)
3) Все слагаемые заключить в скобки
Например: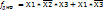 
⟂ 
Проверка: 
+ 
=
Х1* 
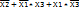
и 
Функция выражение через 
Х1*Х2 
1. Опреация с const
Х↓0= 
= 
Х↓1 = 0
Х↓Х = 
Х↓ 
Стрелка Пирса
* 
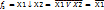В общем смысле Х1*Х2…Хn = (X1↓X1) ↓ (X2↓X2)↓…↓ (Xn↓Xn) = (X1↓0)↓ (X2 ↓ 0)↓… (Xn↓0)
3. Связь с дизьюнкцией
Х1+Х2=(Х1+Х2)*(Х1+Х2) = 
*(
= 
= 
В общем смысле Х1+Х2+…Хn = (Х1↓Х2↓…↓Хn) ↓0
4. Формулы упрощения:
1) 
2) 
Вывод: чтобы любую ФАЛ представить в базисе ИЛИ-НЕ надо выполнить следующее:
1) Записать ФАЛ в КНФ
2) Все знаки сложения и умножения заменить на ↓
3) Все сомножители заключить в скобки
Например: 
=X2
Z=(
=
=X2 * X3 +X2 
4 (X1+X2)=
X2X3+X2 
+X1 
Перейдем ФАЛ в базис «И-НЕ», для этого надо:
1) Представить функцию в ДНФ
2) Все знаки сложения и умножения заменить на знак И-НЕ (⟂)
3) Все слагаемые заключить в скобки
Тогда, Z=(X2⟂X3) ⟂(X2⟂ 
Синтез комбинационных схем со многими выходами
Пример: синтезировать схему автомата
Выполним преобразование
Z1*Z2=X1*X2*X3=Z3
Z1+Z2=X1+X2=Z4
