Определение производной.
Предел отношения приращения функции 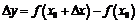 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 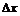 при
при 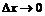
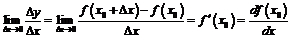
называется производной от функции 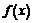 в точке
в точке 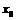 .
.
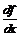 - обозначение Лейбница,
- обозначение Лейбница, 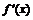 - обозначение Лагранжа.
- обозначение Лагранжа.
Понятие бесконечной производной
Если в точке 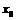 предел
предел 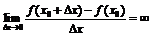 , то
, то
говорят, что функция 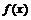 имеет в этой точке бесконечную производную.
имеет в этой точке бесконечную производную.
Здесь бесконечный предел понимается как один из символов 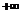 или
или 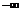 .
.
Определение односторонних производных.
Пределы (конечные или бесконечные) 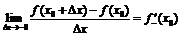 ,
, 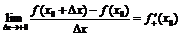 называются соответственно левой и правой производными функции
называются соответственно левой и правой производными функции 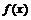 в точке
в точке 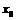 .
.
Имеет место
Теорема.
Для того чтобы функция 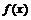 имела в точке
имела в точке 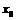 производную
производную 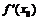 , необходимо и достаточно, чтобы она имела в этой точке как левую, так и правую производные, и чтобы эти производные были равны:
, необходимо и достаточно, чтобы она имела в этой точке как левую, так и правую производные, и чтобы эти производные были равны: 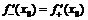 .
.
Пример 1. Исходя из определения производной, найдем производные ряда элементарных функций:
1) 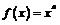 ; 2)
; 2) 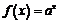 ,
, 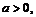
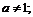 3)
3) 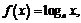
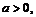
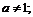 4)
4) 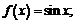 5)
5) 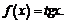
1) Пусть 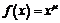 , где
, где 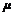 – любое действительное число. Придадим любой точке
– любое действительное число. Придадим любой точке 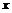 из
из 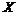 приращение
приращение 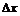
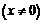 . Новое значение
. Новое значение 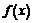 будет
будет 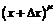 , а для приращения
, а для приращения 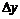 получим:
получим:
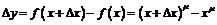 ,
,
так что 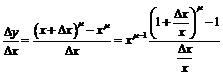 . Если воспользоваться значением предела
. Если воспользоваться значением предела 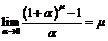 , то для производной данной функции имеем значение:
, то для производной данной функции имеем значение:
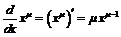 .
.
Для частного случая 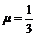 найдём производную в точке
найдём производную в точке 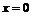 :
: 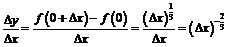 .
.
Видим, что предел этого отношения при 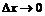 будет равен
будет равен 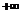 . Если же
. Если же  , то
, то 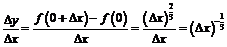 , и в точке
, и в точке 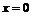 производная слева будет равна
производная слева будет равна 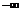 , а справа
, а справа 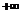 .
.
2) Рассмотрим показательную функцию 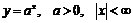 . Составим отношение:
. Составим отношение:
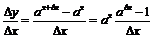 .
.
Так как 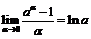 , то
, то 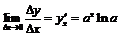 . Если
. Если 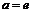 , то приходим к формуле:
, то приходим к формуле:
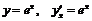 .
.
3) Найдем производную логарифмической функции
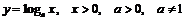 .
.
Для отношения приращения функции к приращению аргумента будем иметь:
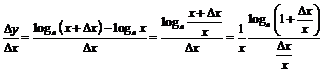 .
.
Используя значение предела 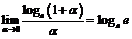 , находим
, находим
 ,
,
при 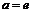
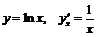 .
.
4) Рассмотрим 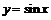 .
.
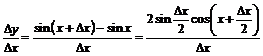 .
.
В силу первого замечательного предела 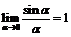 находим, что производная функции
находим, что производная функции 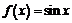 равна
равна 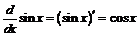 .
.
|
|
5) Для функции 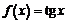 получим:
получим:
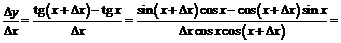
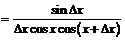 , откуда переходя к пределу при
, откуда переходя к пределу при 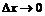 и вновь учитывая первый замечательный предел, имеем:
и вновь учитывая первый замечательный предел, имеем:
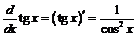 .
.
Пример 2. Исходя из определения производной, покажем, что производная чётной функции есть функция нечётная и наоборот. Пусть 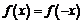 . Возьмем
. Возьмем 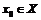 и составим предел отношения:
и составим предел отношения:
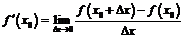 .
.
В данном равенстве заменим 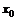 на
на 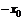 :
:

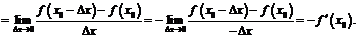
При этом мы воспользовались чётностью функции 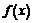 . Тогда
. Тогда 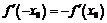 . Совершенно аналогично показывается, что производная нечётной функции
. Совершенно аналогично показывается, что производная нечётной функции 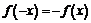 есть функция чётная. Действительно,
есть функция чётная. Действительно,
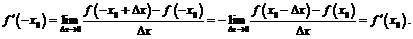
В приведённых примерах для отыскания производной мы пользовались лишь определением. Однако нерационально и практически невозможно находить производную по определению в сложных случаях. Сформулируем основные правила, позволяющие вычислить производную суммы, разности, произведения, частного функций, а также производную суперпозиции функций.
Теорема (правила вычисления производных).
Пусть функции 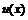 и
и 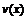 имеют в точке
имеют в точке 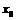 конечную производную, причем
конечную производную, причем 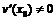 . Тогда:
. Тогда:
1) 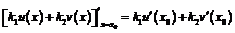 , где
, где 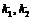 - любые постоянные;
- любые постоянные;
2) 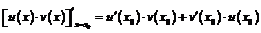 ;
;
3) 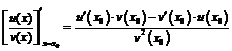 .
.
Эти правила распространяются на любое конечное число слагаемых или сомножителей.
В частности, если 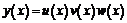 , то
, то
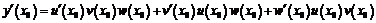 .
.
В общем виде, если 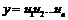 , то
, то
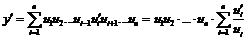 .
.
Теорема о дифференцировании сложной функции.
Пусть функция 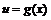 имеет производную
имеет производную 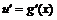 , а функция
, а функция 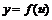 имеет производную
имеет производную 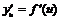 в точках
в точках 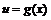 . Тогда производная сложной функции
. Тогда производная сложной функции 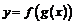 находится по формуле
находится по формуле
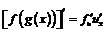 ,
, 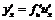 .
.
Определение дифференцируемости функции.
Функция 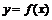 называется дифференцируемой в точке
называется дифференцируемой в точке 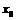 , если её приращение в этой точке представимо в виде:
, если её приращение в этой точке представимо в виде:
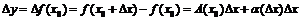 ,
,
где 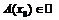 , а
, а 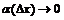 при
при 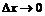 .
.
Очевидно, что второе слагаемое в этом равенстве может быть записано в виде: 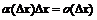 .
.
|
|
Имеет место следующая теорема: