Определение.
Пусть функция 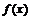 определена всюду в некоторой окрестности точки
определена всюду в некоторой окрестности точки 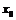 . Говорят, что функция
. Говорят, что функция 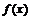 имеет в точке
имеет в точке 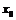 локальный максимум (минимум), если найдётся такая окрестность точки
локальный максимум (минимум), если найдётся такая окрестность точки 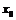 , в пределах которой значение
, в пределах которой значение 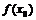 является наибольшим (наименьшим) среди всех других значений этой функции:
является наибольшим (наименьшим) среди всех других значений этой функции: 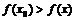
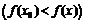 .
.
Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.
Из определения следует, что функция 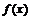 задана по обе стороны от точки
задана по обе стороны от точки 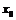 .
.
Пусть функция 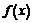 в интервале
в интервале 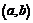 имеет конечную производную. Если в точке x 0 функция имеет экстремум, то применяя к интервалу
имеет конечную производную. Если в точке x 0 функция имеет экстремум, то применяя к интервалу 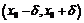 теорему Ферма, имеем
теорему Ферма, имеем 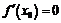 . Это и будет необходимым условием экстремума, и отыскивать его нужно только в тех точках, где производная обращается в нуль; такие точки называются стационарными. Однако не во всякой стационарной точке функция достигает экстремума, и условие
. Это и будет необходимым условием экстремума, и отыскивать его нужно только в тех точках, где производная обращается в нуль; такие точки называются стационарными. Однако не во всякой стационарной точке функция достигает экстремума, и условие 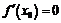 есть необходимое, но не является достаточным. Если
есть необходимое, но не является достаточным. Если 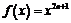 , n – целое, то ее производная
, n – целое, то ее производная 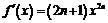 обращается в нуль при
обращается в нуль при 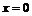 , но в данной точке функция экстремума не имеет: она возрастает в окрестности этой точки.
, но в данной точке функция экстремума не имеет: она возрастает в окрестности этой точки.
Если отказаться от требований существования двусторонней производной, то класс функций 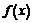 , для которых имеет место экстремум, можно существенно расширить. Для функции
, для которых имеет место экстремум, можно существенно расширить. Для функции  минимум достигается при
минимум достигается при 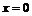 , в то время как производная
, в то время как производная 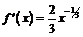 стремится к
стремится к 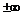 , когда
, когда 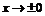 . Аналогично, для функции
. Аналогично, для функции 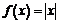 : она достигает минимума при
: она достигает минимума при 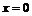 , хотя двусторонняя производная не существует.
, хотя двусторонняя производная не существует.
Поэтому к точкам, подозрительным на экстремум, будем относить стационарные точки, в которых производная обращается в нуль, и точки, в которых двусторонняя производная не существует.
Теорема 1 о достаточных условиях экстремума.
Пусть функция 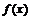 дифференцируема на
дифференцируема на 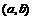 кроме, может быть, точки
кроме, может быть, точки 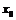 , в которой, однако, непрерывна. Если производная
, в которой, однако, непрерывна. Если производная 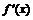 меняет знак при переходе через точку
меняет знак при переходе через точку 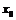 , то данная точка является точкой строгого экстремума. При этом если при
, то данная точка является точкой строгого экстремума. При этом если при 
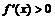 , а при
, а при 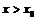
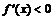 , то в точке
, то в точке 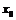 реализуется максимум, если при
реализуется максимум, если при 
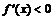 , а при
, а при 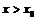
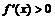 , то функция имеет в точке
, то функция имеет в точке 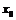 минимум. Если же в пределах указанной окрестности производная не меняет знака, то в точке
минимум. Если же в пределах указанной окрестности производная не меняет знака, то в точке 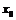 экстремума нет.
экстремума нет.
При исследовании функции на экстремум можно использовать не только смену знака  в окрестности стационарной точки x 0, но и значение
в окрестности стационарной точки x 0, но и значение 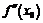 , если оно существует. Пусть
, если оно существует. Пусть 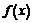 в точке x 0 имеет производную
в точке x 0 имеет производную 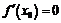 . Если
. Если 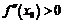 , то в окрестности точки x 0 производная
, то в окрестности точки x 0 производная  возрастает, иначе говоря, она меняет знак с минуса на плюс, следовательно, в этой точке достигается минимум. Если же
возрастает, иначе говоря, она меняет знак с минуса на плюс, следовательно, в этой точке достигается минимум. Если же 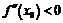 , то
, то  в окрестности точки x 0 убывает, меняя знак с плюса на минус – максимум.
в окрестности точки x 0 убывает, меняя знак с плюса на минус – максимум.
Теорема 2 о достаточных условиях экстремума.
Пусть функция 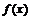 имеет в точке
имеет в точке 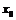 производные до порядка
производные до порядка 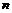 включительно. Тогда, если
включительно. Тогда, если
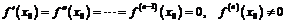 ,
,
то при чётном 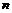 функция имеет в точке
функция имеет в точке 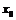 строгий экстремум, а именно: максимум при
строгий экстремум, а именно: максимум при 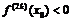 и минимум при
и минимум при 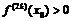 . Если же
. Если же 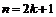 , то экстремума в точке
, то экстремума в точке 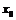 нет.
нет.
Например, для функций 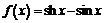 и
и  последовательно находим
последовательно находим



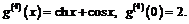
В первом случае экстремума нет, во втором 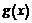 достигает минимума:
достигает минимума: 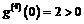 .
.
Пусть функция 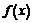 определена и непрерывна в промежутке
определена и непрерывна в промежутке 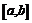 . В прикладных задачах часто требуется указать наибольшее или наименьшее значения в этом промежутке, ведь согласно 2-й теореме Вейерштрасса они существуют. Если, например, наибольшее значение достигается во внутренней точке, то оно будет одним из максимумов (наибольшим). Но наибольшее значение может достигаться и на одном из концов промежутка. Необходимо сравнить между собой все максимумы (если их несколько) и граничные значения
. В прикладных задачах часто требуется указать наибольшее или наименьшее значения в этом промежутке, ведь согласно 2-й теореме Вейерштрасса они существуют. Если, например, наибольшее значение достигается во внутренней точке, то оно будет одним из максимумов (наибольшим). Но наибольшее значение может достигаться и на одном из концов промежутка. Необходимо сравнить между собой все максимумы (если их несколько) и граничные значения 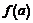 и
и 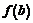 , наибольшее из этих чисел и будет наибольшим значением функции
, наибольшее из этих чисел и будет наибольшим значением функции 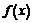 в
в 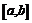 .
.
Пример 1. Исследовать на экстремум функцию: 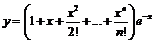 ,
, 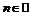 .
.
Найдем производную: 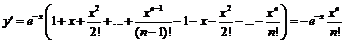 ,
,
Производная обращается в нуль при 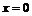 . По теореме 1 легко установить, что в точке
. По теореме 1 легко установить, что в точке 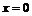 реализуется максимум, если
реализуется максимум, если 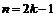 (в этом случае
(в этом случае 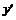 при переходе через точку
при переходе через точку 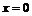 меняет знак с плюса на минус), если же
меняет знак с плюса на минус), если же 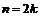 экстремума нет, ибо
экстремума нет, ибо 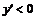 в окрестности критической точки.
в окрестности критической точки.
Пример 2. Исследовать на экстремум в точке 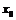 функцию
функцию 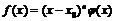 , где
, где 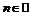 , а функция
, а функция 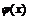 непрерывна при
непрерывна при 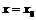 и
и 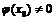 .
.
Воспользуемся определением и исследуем знак приращения функции в точке 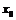 :
: 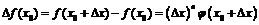 .
.
Очевидно, что наличие или отсутствие экстремума будет определяться чётностью или нечётностью натурального числа 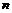 , так как по непрерывности
, так как по непрерывности 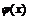 существует такая окрестность точки
существует такая окрестность точки 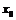 , в пределах которой
, в пределах которой 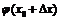 имеет тот же знак, что и
имеет тот же знак, что и 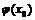 . Если
. Если 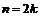 , то в указанной окрестности
, то в указанной окрестности 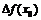 имеет тот же знак, что и
имеет тот же знак, что и 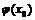 :
: 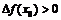 , если
, если 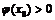 - в точке
- в точке 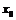 минимум;
минимум; 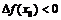 , если
, если 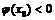 - в точке
- в точке 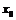 максимум. Если же
максимум. Если же 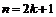 , то экстремума нет, так как значение
, то экстремума нет, так как значение 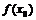 не является ни наименьшим, ни наибольшим в окрестности рассматриваемой точки. Отметим, что воспользоваться теоремой 1 здесь нельзя, ибо условия задачи не позволяют найти производную функции
не является ни наименьшим, ни наибольшим в окрестности рассматриваемой точки. Отметим, что воспользоваться теоремой 1 здесь нельзя, ибо условия задачи не позволяют найти производную функции 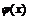 , а значит и
, а значит и 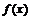 .
.
Пример 3. Исследовать на экстремум функцию 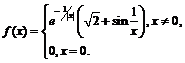
В точке 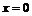 проведём исследование по определению:
проведём исследование по определению:
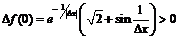 для любого
для любого 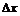 , следовательно, это точка минимума функции:
, следовательно, это точка минимума функции: 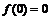 .
.
Для значений 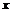 , отличных от нуля, вычислим производную:
, отличных от нуля, вычислим производную:
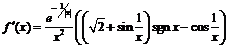 . Производная обращается в нуль в точках, где
. Производная обращается в нуль в точках, где 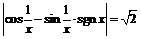 . Однако, так как
. Однако, так как  , то при переходе через указанные точки производная знака не меняет. Следовательно, единственной точкой экстремума данной функции является точка
, то при переходе через указанные точки производная знака не меняет. Следовательно, единственной точкой экстремума данной функции является точка 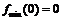 .
.
Пример 4. Найти наименьшее и наибольшее значения функции  на отрезке
на отрезке 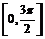 .
.
Исследуем функцию на экстремум. Для этого решим уравнение
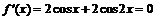
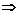
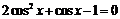
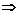
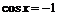 ,
, 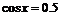
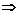
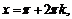
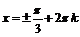 ,
, 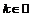 . Отрезку
. Отрезку 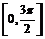 принадлежат две стационарных точки:
принадлежат две стационарных точки: 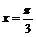 и
и  . Для проверки достаточных условий воспользуемся теоремой 2:
. Для проверки достаточных условий воспользуемся теоремой 2: 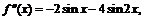
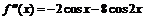 . В точке
. В точке 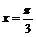 имеем максимум, так как
имеем максимум, так как 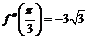 ,
, 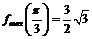 , а в точке
, а в точке  экстремума нет, ибо
экстремума нет, ибо 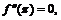 а
а 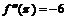 . В граничных точках промежутка функция принимает значения:
. В граничных точках промежутка функция принимает значения: 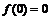 и
и 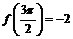 . Сравнивая эти значения со значением в точке экстремума, приходим к выводу, что наименьшее значение на указанном отрезке функция принимает в точке
. Сравнивая эти значения со значением в точке экстремума, приходим к выводу, что наименьшее значение на указанном отрезке функция принимает в точке 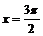 , а наибольшее – в точке
, а наибольшее – в точке 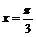 :
: 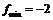 ,
, 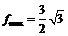 .
.
Пример 5. Доказать неравенство: 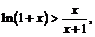
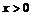 .
.
Рассмотрим функцию:  на интервале
на интервале 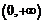 . Исследуем её на экстремум. Производная
. Исследуем её на экстремум. Производная 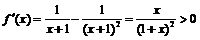 на рассматриваемом промежутке, поэтому функция возрастает и для
на рассматриваемом промежутке, поэтому функция возрастает и для  имеет место неравенство:
имеет место неравенство: 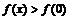 , но
, но 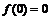 , следовательно,
, следовательно, 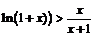 .
.
Задачи, приводящие к исследованию на экстремум, имеют большое теоретическое и прикладное значение. Требование, чтобы некоторая величина принимала экстремальное значение, приводит к формулировкам законов естествознания.
Пример 6. В оптике принцип Ферма, состоящий в том, что луч света распространяется по траектории, требующей минимум времени, приводит к двум законам геометрической оптики.
Пусть луч, скорость которого V, падает из точки A и, отразившись от оси Ox в точке с координатой 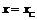 , приходит в точку B. Длина ломаной
, приходит в точку B. Длина ломаной 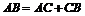 будет равна
будет равна 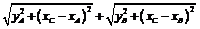 . Тогда время прихода луча в точку B определится формулой
. Тогда время прихода луча в точку B определится формулой
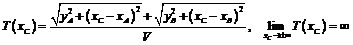 .
.
Найдем точку 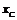 экстремума функции
экстремума функции 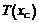 , так как время, затраченное лучом на прохождение ломаной ACB должно быть минимальным:
, так как время, затраченное лучом на прохождение ломаной ACB должно быть минимальным:
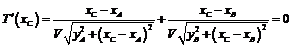 ,
,
откуда 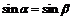 , или угол падения луча равен углу отражения.
, или угол падения луча равен углу отражения.
Пусть ось Ox есть граница двух сред, в которых скорость распространения света, соответственно V 1 и V 2. Тогда длина пути в первой среде 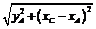 , во второй
, во второй 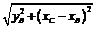 . Время прохождения всего пути ACB будет равно
. Время прохождения всего пути ACB будет равно
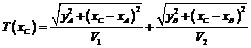 .
.
Требование минимальности этого времени дает
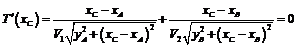
или
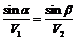 .
.
Это известный закон преломления света.