Ответ:
;
Задача 2. В опыте Юнга интерференционная картина по мере удаления от середины размывается, и при k = 4 полосы исчезают. Почему?
Решение:
В опыте Юнга интерференционная картина представляет чередование интерференционных максимумов и минимумов в виде полос, параллельных щелям S1 и S2. В центре интерференционной картины расположена светлая полоса (k = 0). По обе стороны от центральной полосы расположены максимумы ±1, ±2, ±3, ±4 порядков интерференции. Разность хода между интерферирующими волнами по мере удаления от центральной полосы увеличивается. При этом по мере удаления от центра ухудшается видность и четкость интерференционной картины, полосы размываются и исчезают, по условию последний максимум наблюдается при k = 4. Исчезновение полос означает, что колебания, пришедшие от двух источников S1 и S2, некогерентны. Пока их разность хода не превышала 4 λ, они были когерентны. Следовательно, максимальная разность хода, при которой наблюдается интерференция, будет равна:
;
Величина 
называется длиной когерентности. Если оптическая разность хода превышает длину когерентности, интерференционная картина не наблюдается.
Задача 3. Покажите, что при преломлении в призме с малым преломляющим углом α и показателем преломления n луч отклоняется на угол δ ≈(n - 1)α независимо от угла падения, если угол падения также мал. Призма находится в воздухе, n0 = 1.
Решение:
По построению δ-внешний угол треугольника DCB (рис. 2), он равен сумме внутренних углов, не смежных с ним:
δ= φ- β+ β1- φ1;
Согласно закону преломления,
.
По условию угол φ, а значит и β малы, то есть Sinφ≈φ, Sinβ≈β, (выраженному в радианах), тогда nβ=φ, nφ1=β1. Подставив значения φ и β1 в формулу для δ, получим:
.
Из треугольника СВК: β+φ1=α (α- внешний угол, равный преломляющему углу призмы по построению). Таким образом,
.
Задача 4. Найдите число полос интерференции N, получающихся с помощью бипризмы, если показатель преломления бипризмы n = 1,5, преломляющий угол 
рад, длина волны источника λ=600 нм. Расстояние от источника до бипризмы равно а = 1 м, расстояние от бипризмы до экрана равно b = 4 м.
Решение:
Лучи от источника S, падающие на бипризму, после преломления отклоняются от первоначального направления на угол δ≈α(n-1) (см. Задача 3). Продолжение этих лучей до точки пересечения дает изображение двух мнимых источников S1 и S2 (рис. 3). Они являются когерентными источниками, поэтому в области перекрытия АВ когерентных волн, распространяющихся от этих источников, на экране наблюдается интерференционная картина в виде чередующихся темных и светлых полос, как и в опыте Юнга. Центральный максимум интерференционной картины (k = 0) проходит через точку О экрана. Максимумы более высоких порядков находятся на расстоянии yk от центра (см. Задача 1).
Ширина полосы:
.
Здесь L=a+b расстояние от источников до экрана, d - расстояние между мнимыми источниками. Из треугольника SS1K:
.
Тогда ширина интерференционной полосы:
.
Число интерференционных полос в области интерференции АВ равно:
.
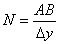Величину области перекрытия АВ найдем из подобных треугольников CS1S и СОВ:
.
Число наблюдаемых полос интерференции будет равно:
.
Ответ: .
Задача 5. В опыте Ллойда (рис. 4) световая волна, исходящая непосредственно из источника S (узкой щели), интерферирует с волной, отраженной от зеркала 3. В результате на экране Э образуется система интерференционных полос. Расстояние от источника до экрана L = 100 см. При некотором положении источника ширина интерференционной полосы на экране Δу = 0,25 мм, а после того как источник отодвинули от плоскости зеркала на h = 0,6 мм, ширина полос уменьшилась в η= 1,5 раза. Найдите длину λ световой волны.
Решение: В точке М интерферируют две когерентные волны 1 и 2, исходящие из источника S. По построению волну 2 можно считать исходящей из источника, 
, являющегося мнимым изображением источника S в зеркале 3. Они симметрично расположены относительно плоскости зеркала, обозначим расстояние между ними 
. Если зеркало S отодвинуть на h, то новое расстояние между 
равно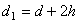 
(рис. 5). Для определения длины волны λ используем выражение для ширины полосы из опыта Юнга, применив его для двух расстояний между источниками.
