Лекция ДО_5
Магнитогидродинамическое описание плазмы
1. Одножидкостная МГД
В этом случае плазма рассматривается как единое целое, без разбиения на компоненты – ионы и электроны. Поскольку движение ионов и электронов не может происходить независимо (должна соблюдаться квазинейтральность ne = ni = n), гидродинамическая скорость фактически соответствует скорости тяжелой компоненты, а электроны движутся вместе с ионами.
Система уравнений включает в себя:
а) уравнение неразрывности
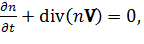 (1)
(1)
б) уравнение движения
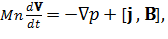 (2)
(2)
где M = масса иона, p – давление, j – плотность тока в плазме,
в) уравнение состояния
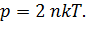 (3)
(3)
Поскольку масса электрона m << M, можно считать массовую плотность ρ = M n.
В уравнении движения пренебрегается вязкостью. В рамках данной модели мы ограничились изотермическим приближением, поэтому уравнение энергии не записано.
К соотношениям (1) - (3) добавляется система уравнений Максвелла
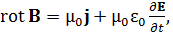 (4)
(4)
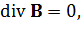 (5)
(5)
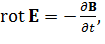 (6)
(6)
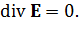 (7)
(7)
И, наконец, записывается закон Ома
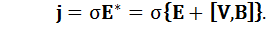 (8)
(8)
2. Двухжидкостная МГД
Если в одножидкостном приближении за скорость плазмы принимается скорость ионов, то здесь рассматривается движение отдельно ионной и электронной компонент со скоростями 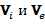 соответственно. Это приближение применяют, если необходим учет относительного движения компонент.
соответственно. Это приближение применяют, если необходим учет относительного движения компонент.
Вместо (1), (2) записываются отдельно уравнения для ионов и электронов. Приведем их для случая Z = 1 (при этом также выполняется условие квазинейтральности ne = ni = n):
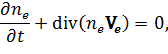
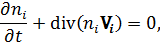
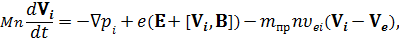
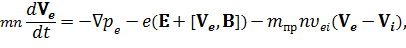
где 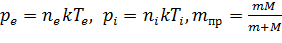 – приведенная масса,
– приведенная масса, 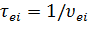 – среднее время между электронно-ионными столкновениями.
– среднее время между электронно-ионными столкновениями.
происходить независимо (должна соблюдаться квазинейтральность ne = ni = n), гидродинамическая фактически соответствует скорости тяжелой компоненты, а электроны движутся вместе с ионами.
Т.к. m << M, инерционный член в последнем уравнении обычно опускают. Если это сделать и сложить два последних уравнения, можно получить обобщенный закон Ома:
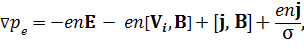
где 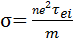 – электропроводность плазмы,
– электропроводность плазмы, 
Слагаемое 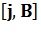 приводит к появлению составляющей плотности тока, нормальной к плоскости E, B. Это явление – эффект Холла, а соответствующая составляющая – холловский ток.
приводит к появлению составляющей плотности тока, нормальной к плоскости E, B. Это явление – эффект Холла, а соответствующая составляющая – холловский ток.
По сравнению с одножидкостной МГД в этой модели учитываются градиент электронного давления и эффект Холла.
Естественно, к рассмотренным гидродинамическим уравнения также добавляются уравнения Максвелла.
ВМОРОЖЕННОСТЬ МАГНИТНОГО ПОЛЯ В ПЛАЗМУ
При движении плазмы с очень высокой электропроводностью имеет место замечательное свойство «приклеенности» магнитных силовых линий: при движении плазмы силовые линии следуют за ней, будучи как бы «вморожены» в плазму. Свойство вмороженности существенно облегчает анализ сил со стороны магнитного поля, возникающих при смещении плазмы от первоначального равновесного состояния. Тем самым значительно упрощается анализ устойчивости равновесных состояний плазмы.
Факт вмороженности магнитного поля в идеально проводящую плазму был установлен основателем магнитной гидродинамики Х. Альфвеном. Логика здесь была следующей.
Пусть плазма с очень высокой электропроводностью σ движется со скоростью 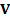 и при этом в ней имеется магнитное поле, характеризующееся напряженностью магнитного поля H (при рассмотрении данного раздела будем использовать систему единиц СГС, т.к. большинство положений по вмороженности приводится различными авторами именно в этой системе единиц).
и при этом в ней имеется магнитное поле, характеризующееся напряженностью магнитного поля H (при рассмотрении данного раздела будем использовать систему единиц СГС, т.к. большинство положений по вмороженности приводится различными авторами именно в этой системе единиц).
Тогда на заряженную частицу плазмы должна действовать сила Лоренца
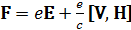 ,
,
где е – заряд частицы, Е – напряженность электрического поля.
На электроны и ионы, имеющие противоположные заряды, соответствующие силы действуют в разные стороны, т.е. они должны приводить к возбуждению электрического тока. Но если проводимость σ очень велика, т.е. практически бесконечна, то при любой конечной величине генерируемого тока величина силы F должна быть исчезающее мала. Это значит, что в идеально проводящей среде (идеальная одножидкостная магнитная гидродинамика) электрическое поле подстраивается под величину
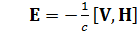 . (9)
. (9)
Но тогда из уравнения Максвелла 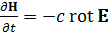 следует соотношение
следует соотношение
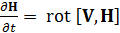 . (10)
. (10)
Оказывается, что это уравнение устанавливает закон вмороженности магнитного поля в плазму. Оно описывает свойство вмороженности при течении плазмы в электромагнитных полях сложных конфигураций.
Наиболее просто это видно в двумерном случае, который будет представлять для нас особый интерес при дальнейшем рассмотрении процесса перезамыкания магнитных силовых линий, который имеет очень большое значение в термоядерных системах.
Пусть V и H в декартовой системе координат х, у, z имеют только х - и у - компоненты. Тогда в силу 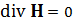 вектор напряженности магнитного поля можно представить в виде H
вектор напряженности магнитного поля можно представить в виде H 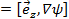 , где
, где 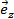 - единичный вектор, направленный вдоль оси О z.
- единичный вектор, направленный вдоль оси О z.
При этом ψ – функция потока магнитного поля, H 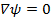 , т.е. ψ= const на силовой линии. Если же подставить определение H через
, т.е. ψ= const на силовой линии. Если же подставить определение H через 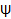 в уравнение вмороженности, то оно примет вид:
в уравнение вмороженности, то оно примет вид:
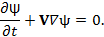
Однако это означает, что субстанциальная производная 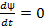 , т.е. ψ переносится вместе с плазмой.
, т.е. ψ переносится вместе с плазмой.
Преобразуем уравнение (10). Для этого раскроем тройное векторное произведение 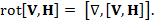 Такую процедуру мы с Вами уже выполняли, решая уравнение движения независимых заряженных частиц и находя общее выражение для скорости дрейфа. Однако в данном случае есть принципиальная особенность такого преобразования, связанная с дуализмом оператора
Такую процедуру мы с Вами уже выполняли, решая уравнение движения независимых заряженных частиц и находя общее выражение для скорости дрейфа. Однако в данном случае есть принципиальная особенность такого преобразования, связанная с дуализмом оператора 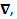 который обладает и дифференциальными и векторными свойствами. Именно в этой ситуации, когда одним из сомножителей является оператор Гамильтона
который обладает и дифференциальными и векторными свойствами. Именно в этой ситуации, когда одним из сомножителей является оператор Гамильтона 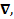 по правилам векторного анализа тройное векторное произведение сводится к сумме не двух, а четырех слагаемых:
по правилам векторного анализа тройное векторное произведение сводится к сумме не двух, а четырех слагаемых:
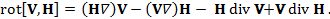
C учетом того, что из уравнений Максвелла 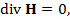 получаем
получаем
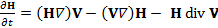 .
.
Вводя субстанциальную производную 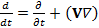 , и перенося второе слагаемое из правой части последнего уравнения в его левую часть, получим
, и перенося второе слагаемое из правой части последнего уравнения в его левую часть, получим
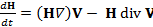 . (11)
. (11)
Воспользуемся далее уравнением неразрывности
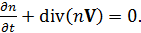 (12)
(12)
Раскрывая оператор дивергенции от произведения скалярной величины на векторную, получим
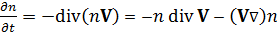 .
.
Учитывая выражение для субстанциальной производной, из последнего соотношения следует
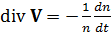 . (13)
. (13)
Тогда уравнение (11) примет вид 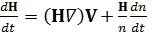 или
или
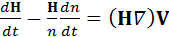 . (14)
. (14)
Для дальнейшего преобразования уравнения (14) рассмотрим следующее соотношение:
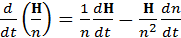 .
.
Обратим внимание, что левая часть (14) отличается от правой части последнего уравнения только множителем 1/ n. Тогда
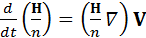 . (15)
. (15)
Рассмотрим некоторые частные случаи течения плазмы в магнитном поле.
1. В простейшей ситуации, когда скорость движения плазмы меняется только в направлении, перпендикулярном вектору напряженности магнитного поля, правая часть уравнения (15) равна нулю, и следовательно
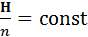 . (16)
. (16)
Этот случай имеет место, в частности, при плоском (одномерном) сжатии плазмы поперек магнитного поля.
2. При радиальном сжатии поперек магнитного поля (например, в коаксиальном ускорителе) полученное соотношение несколько меняется и принимает вид
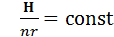 . (17)
. (17)
3. При одномерном сжатии плазмы вдоль магнитного поля из уравнения (15) получим
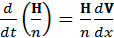 ,
,
где х – координата вдоль вектора напряженности магнитного поля.
Уравнение неразрывности для этого случая представляется следующим образом:
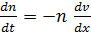 .
.
Тогда 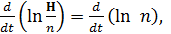 откуда, проинтегрировав, получим, что
откуда, проинтегрировав, получим, что  пропорционально
пропорционально  , т.е.
, т.е.
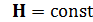 . (18)
. (18)
Полученные для рассмотренных трех случаев левые части выражений (16)-(18) называют параметрами вмороженности.
В заключение настоящего раздела отметим еще раз, что все результаты, касающиеся вмороженности магнитного поля в плазму, получены Х. Альфвеном только для идеально проводящей плазмы в одножидкостном МГД-приближении. Однако этот подход оказался очень привлекательным для проведения аналогий рассматриваемых явлений с классической механикой, что позволило, например, при исследовании течений плазмы интерпретировать магнитные силовые линии как обычные нити с возможностью изменения их натяжения. Обратим внимание, что из уравнения (9) следует выражение для скорости дрейфа в скрещенных электрическом и магнитном полях (в системе СГС оно имеет вид 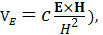 знакомое нам по модели независимых частиц и выведенное совершенно при других предположениях.
знакомое нам по модели независимых частиц и выведенное совершенно при других предположениях.
Учет конечной проводимости плазмы
При выводе параметров вмороженности для идеально проводящей плазмы предполагалось выполнение соотношения (9). Учет конечной проводимости позволяет исследовать явление диффузии магнитного поля в плазму.
В этом случае (используя более широко применяемую систему единиц СИ) из закона Ома
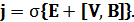
можно выразить напряженность электрического поля 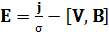 и подставить ее в уравнение Максвелла
и подставить ее в уравнение Максвелла 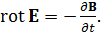
Тогда для производной от индукции магнитного поля по времени получим следующее выражение:
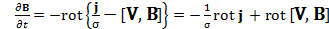 . (19)
. (19)
Обратим внимание, что при σ →∞ первое слагаемое в правой части (19) обращается в нуль, и мы получаем такое же уравнение вмороженности, как (10), но только в системе СИ для вектора магнитной индукции B.
Продолжая вывод, используем другое уравнение Максвелла – уравнение (4) в отсутствие токов смещения:
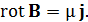
Выразим отсюда плотность тока и для подстановки в (19) возьмем операцию rot от левой и правой частей этого выражения
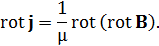
Раскрывая тройное векторное произведение в правой части, получим
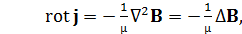 (20)
(20)
где ∆ – оператор Лапласа.
Подставляя выражение (20) в уравнение (19), представим его в следующем виде:
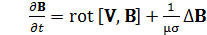 . (21)
. (21)
Второе слагаемое с оператором Лапласа характеризует процесс диффузии магнитного поля в плазму
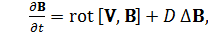 (22)
(22)
где коэффициент диффузии  .
.
Глубина проникновения магнитного поля в плазму определяется коэффициентом диффузии и временем процесса:
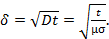 (23)
(23)
Оценим характерные масштабы этой величины для термоядерных установок с магнитным удержанием. Для требуемых температур плазмы масштаба 10 кэВ коэффициент электропроводности составляет ~ 109 1/(Ом м). Подставляя эту величину и значение магнитной проницаемости вакуума в (23), в системе СИ получим:
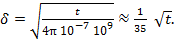 (24)
(24)
Для токамака ИТЭР и характерного времени 400 с получим толщину проникновения магнитного поля в плазму ~ 0,5 м, а для импульсных систем с t ~ 10-6 c – менее 10-4 м.
В заключение настоящей лекции рассмотрим еще 2 вопроса, важных для термоядерных систем с магнитным удержанием, которые вытекают из анализа процессов в МГД-приближении.
Параметр β
Когда мы рассматривали основные отличия высокотемпературной плазмы от низкотемпературной, было отмечено большое влияние параметра β (отношения магнитного давления к газокинетическому) на процессы в термоядерных системах.
Определение этого параметра связано с условием рассмотрения равновесия плазменного образования в магнитном поле. В этом случае при равенстве нулю производной от скорости по времени уравнение движения плазмы в одножидкостном приближении (2) принимает следующий вид:
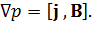 (25)
(25)
Выражая плотность тока из уравнения Максвелла (4) и пренебрегая токами смещения, из (25) получим:
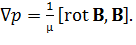 (26)
(26)
Раскрывая, как и ранее, тройное векторное произведение в правой части, соотношение (26) преобразуем к следующему виду:
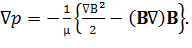 (27)
(27)
Второе слагаемое в правой части этого уравнения обращается в нуль, если магнитные силовые линии – прямые или градиент магнитного поля перпендикулярен вектору магнитной индукции.
В этом случае, интегрируя последнее уравнение, получим
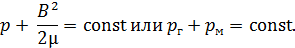
Таким образом, сумма газокинетического и магнитного давлений 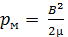 остается постоянной. Этот факт очень часто используется для анализа равновесия в плазме и создания равновесных магнитных конфигураций.
остается постоянной. Этот факт очень часто используется для анализа равновесия в плазме и создания равновесных магнитных конфигураций.
Для характеристики таких конфигураций и используется параметр β:
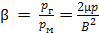 .
.
Этот параметр оказывается очень важным для анализа процессов в магнитных ловушках и устойчивости плазменных образований в них.
При β << 1 «вакуумные» и «плазменные» магнитные поля (т.е. в отсутствие плазмы в системе и в ее присутствии) практически совпадают, а при β ≈ 1 в плазме текут диамагнитные токи и «плазменные» магнитные поля сильно отличаются от «вакуумных».
Ансамбль частиц и полей – плазма как целое
В предыдущем подразделе были упомянуты возникающие в плазме диамагнитные токи, которые могут существенно изменить магнитные поля, создаваемые в магнитных ловушках.
Рассмотрим, как возникают эти токи в простейшем случае, когда имеется прямолинейный разряд, по которому течет некоторый ток I, создающий магнитное поле, вектор которого направлен на нас (Рис. 1).
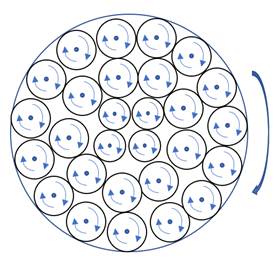 Id
Id
Рис. 1
На рисунке изображены заполняющие сечение разряда прямолинейные магнитные силовые линии. Как видно, внутри рассматриваемой области токи, создаваемые при кольцевом движении заряженных частиц вокруг различных силовых линий, в каждой точке направлены противоположно и компенсируют друг друга. На наружной поверхности разряда такой компенсации нет, в результате чего возникает диамагнитный ток Id. Его направление таково, что создаваемое им осевое магнитное поле направлено противоположно приложенному и ослабляет его. В зависимости от числа заряженных частиц в разряде компенсация внешнего «вакуумного» поля может полной или относительно слабой.
Другую ситуацию, в которой также возникают диамагнитные токи, иллюстрирует рис. 2.
 | |||||
 | |||||
 | |||||



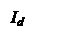
Рис. 2
Этому способствует наличие градиента плотности заряженных частиц (на рис. 2 различной плотности частиц соответствует различная густота окружностей), когда компенсация кольцевых токов также оказывается неполной. Таким образом, различие «вакуумных» и «плазменных» магнитных конфигураций – типичная ситуация в магнитных ловушках и должна подвергаться тщательному анализу для корректного расчета удержания частиц в термоядерных системах.