1.1. Исходные данные на проектирование:
1. Длина главной балки – 16,9 м;
2. Бетон тяжелый класса В40; F= 300; W10;
3. Рабочая арматура:
- обычная - класса А-II;
- напрягаемая - семипроволочные канаты класса – K-7,( -12);
-12);
4. Ездовое полотно:
· Плотный мелкозернистый асфальтобетон: 
 =70 мм;
=70 мм;  =22.60 кН/м3
=22.60 кН/м3
· Защитный слой бетона:  =50 мм;
=50 мм;  =23.50 кН/м3
=23.50 кН/м3
· Гидроизоляция – из двух слоев техноэластмоста:
 =5*2=10 мм;
=5*2=10 мм;  =14.70 кН/м3
=14.70 кН/м3
· Выравнивающий слой бетона:  =40 мм;
=40 мм;  =23.50 кН/м3
=23.50 кН/м3
· Железобетонная плита проезжей части:  =180 мм;
=180 мм;  =24.50 кН/м3
=24.50 кН/м3

Рисунок 1 – Схема нагрузок от подвижного состава
1.2 Определение изгибающих моментов
Таблица 1 – Сбор нагрузок на 1м2 проезжей части
| № п/п | Вид нагрузки | Нормативная Н/м2 | Коэффициент надежности

| Расчетная Н/м2 |
| Мелко-зернистый плотный асфальтобетон 0.07*22600=1582 | 1.50 | |||
| Защитный слой бетона 0.05*23500=1175 | 1.30 | |||
| Гидроизоляция 0.01*14700=147 | 1.30 | |||
| Выравнивающий слой бетона 0.04*23500=940 | 1.30 | |||
| Ж/б плита проезжей части 0.18*24500=4410 | 1.10 |
 =8254 Н/м2
=8254 Н/м2  =10165 Н/м2
=10165 Н/м2
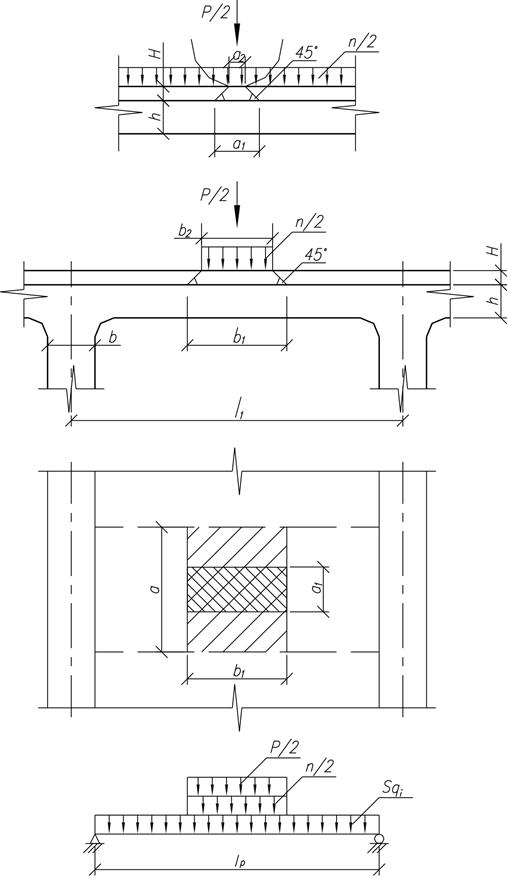
Рисунок 2 – Расчётная схема №1 плиты при lp ≤ 2.0 м
При длине пролета плиты менее 2 м, загружение плиты производится согласно расчетной схеме №1 на рис 2. Балочный изгибающий момент в середине пролета плиты:
 (1)
(1)
Определяем изгибающие моменты от постоянных расчетных нагрузок на 1 п.м. ширины плиты. Момент в середине пролета:
 ; (3)
; (3)
Lp = L1 – b – длина расчетного пролета
Lp = 1,996 – 0.16 = 1,836 (м)
Мgb = 10.165х1,8362 = 4,89 (кН.м)
Так как у нас Lp=1,806м <2 м, то для расчетов будем использовать 1-у колёсную расчётную схему загружения №1 (рис 2).
Определяем изгибающие моменты от временных нагрузок А-14 и НК-100;
Осевая нагрузка распределяется на площадку с размерами:
a1 = а2 + 2Н = 0.20+2х0.17 = 0.54 (м)
b1 = b2 + 2Н = 0.60+2х0.17 = 0.94 (м)
b3 = b2+ 2H+C=0.60+2х0.17+1.10=2.04 (м)
Н=0,17м принята по результатам конструирования ездового полотна.
Рабочая ширина плиты воспринимающая нагрузку 5К равна:
а = а1 + Lp/3 ≥ 2/3 Lp
а = 0.54 + 1,836/3 = 1,15 < 1.22 м; принимаем а=1,22 м.
Динамический коэффициент (1+μ) для расчета элементов проезжей части согласно:
(1+μ) = 1,4
Балочный изгибающий момент в середине пролета плиты:


 -коэффициенты надежности согласно
-коэффициенты надежности согласно
Максимальный изгибающий балочный момент:  ;
;

Расчетные изгибающие моменты с учетом поправочных коэффициентов:
* в середине пролета 
* опорное сечение 
 .
.
Рисунок 3 – Эпюра изгибающих моментов
1.3. Подбор сечений рабочей арматуры плиты

Рисунок 4 – Расчетная схема в середине пролета плиты
Задаёмся диаметром рабочей арматуры – ø 14 мм.
Класс арматуры сетки С-1: А-II Rs=265МПа
Класс бетона В40:  Rb=22.0 МПа
Rb=22.0 МПа
Рабочая высота сечения:  ;
;
аs=0.03 м – толщина защитного слоя бетона

Необходимая площадь сечения рабочей арматуры:
 );
);
b =1.0 м, так как расчеты выполняем на 1 пог. м ширины плиты.

Согласно сортаменту арматуры принимаем сетку С-1 с шагом рабочей арматуры 1000/5=200мм 200/200/14/12 с  см2
см2
Проверка прочности плиты на фактическое армирование:
Высота сжатой зоны:

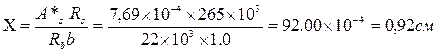
Условие прочности:  ,
,
что больше М=24,95кН*м
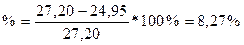 ,что меньше 10%
,что меньше 10%

Рисунок 5 – Расчетная схема в опорном пролета плиты
Задаемся диаметром рабочей арматуры ø 20 мм, класс АII;

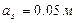
Необходимая площадь рабочей арматуры: 
Согласно сортаменту арматуры принимаем:5 ø 20 с А*S=15,71см2,
что больше минимального значения по расчёту 13,37см2.
Высота сжатой зоны сечения:
 ;
; 
Граничное значение относительной высоты сжатой зоны бетона  :
:

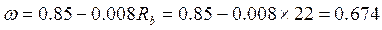
 ;
; 
Граничное значение абсолютной высоты сжатой бетона  :
:

Условие прочности: 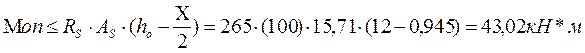
Моп=39,91 > 46,02– условия прочности не выполняется.
Запас прочности:
 %, что меньше допускаемой величины 10%
%, что меньше допускаемой величины 10%
1.4. Проверка прочности плиты по наклонному сечению
Поперечные силы в плите определяют как в разрезной балке. Линию влияния Q строят для двух сечений: в начале и в конец вута (сечение I-I и сечение II-II). Для получения Qmax при загружении линии влияния Q грузовую площадку располагают так, чтобы ее левая грань совпадала с рассматриваемым сечением.


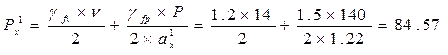 кН
кН
 кН
кН


При назначении толщины плиты следует выполнить условие:
 , т.е. условие прочности плиты следует выполнять без установки поперечной арматуры:
, т.е. условие прочности плиты следует выполнять без установки поперечной арматуры:


 ,
,  МПа
МПа
|

Рисунок 6 – Расчётная схема плиты при расчёте прочности наклонного сечения (Q)
 (2*1.4*103 *1.0*0.1432)/(2*0.143)=200.2 кН, что больше Q=117.38кН. Условие прочности выполняется по бетону.
(2*1.4*103 *1.0*0.1432)/(2*0.143)=200.2 кН, что больше Q=117.38кН. Условие прочности выполняется по бетону.
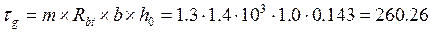 кН
кН
Сопротивление бетона класса скалыванию при изгибе:
Rb,sh = 

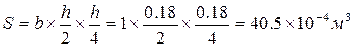


 Условие прочности выполняется, так как
Условие прочности выполняется, так как  . Назначаем толщину плиты 0,18м.
. Назначаем толщину плиты 0,18м.
1.5.Расчет плиты по ширине раскрытия трещин
Плита проезжей части относится к категории 3в по трещиностойкости. Предельное раскрытие трещин Δcr=0,020см. Ширина раскрытия трещин, нормальных к продольной оси:

В середине пролета
Вычисляем площадь взаимодействия бетона и арматуры (рис.11):
Aƞ = b·hS = b·(a3+0.5·dS+6·dS) =100·(3+1,4/2+6·1,4) = 1210 см2

Рисунок 6 – Расчётная схема плиты
Изгибающий момент от нормативных нагрузок:
 Плечо внутренней пары сил:
Плечо внутренней пары сил:

Напряжения в растянутой арматуре:

 - радиус армирования
- радиус армирования
β=1,0 - коэффициент, учитывающий степень сцепления арматуры с бетоном. Для стержневой арматры периодического профиля β=1,0.;
n - количество стержней по ширине плиты b=100см, n=5;
dS - диаметр арматуры
 см
см

Ширина раскрытия трещин находится в пределах допустимой.
В опорном сечении
Вычисляем площадь взаимодействия бетона и арматуры:
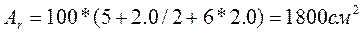
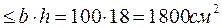


 - радиус армирования
- радиус армирования

 см
см
Ширина раскрытия трещин находится в пределах допустимой.
2. Расчет железобетонного предварительно напряженного пролетного строения.
Пролетное строение в поперечном сечении состоит из 5 бездиафрагменных предварительно напряженных балок заводского стендового изготовления.
Габарит моста Г 8+1х0,75 м, длина балок 16,9 м, расчетный пролет  м.
м.
Высота балок 1.23 м.
Расстояние между осями балок 1996 м.
Материалы: бетон класса В40, ненапрягаемая арматура сталь классов А-II,напрягаемая-семипроволочные канаты К-7 даметром 12
2.1 Расчет постоянных нагрузок на 1п.м. длины балки
Постоянная равномерно распределяется нагрузка:
Нормативный вес асфальтобетона:
 Н/м
Н/м
Расчетный вес асфальтобетона:
 Н/м
Н/м
Нормативный вес гидроизоляции:
 Н/м
Н/м
Расчетный вес гидроизоляции:
 Н/м
Н/м
Нормативный вес выравнивающего слоя:
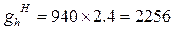 Н/м
Н/м
Расчетный вес выравнивающего слоя:
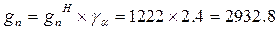 Н/м;
Н/м;
Нормативный вес защитного слоя бетона:
 Н/м
Н/м
Расчетный вес защитного слоя бетона:
 Н/м;
Н/м;
Нормативный вес ж/б плиты проезжей части:
 Н/м
Н/м
Расчетный вес ж/б плиты проезжей части:
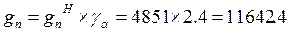 Н/м;
Н/м;
Нормативный вес ограждения безопасности:

 кН/м
кН/м
Расчетный вес ограждения безопасности:
 кН/м
кН/м
Нормативный вес перильного ограждения и карниза:
 кН/м
кН/м
Расчетный вес ограждения:
 кН/м
кН/м
Вес балки:  ;
;
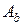 - площадь поперечного сечения балки;
- площадь поперечного сечения балки;  кН/м3- удельный вес железобетона.
кН/м3- удельный вес железобетона.
Для упрощения расчетов действительное сечение балки заменяем на приведенное
Приведенная ширина сжатого пояса (плиты):
 м
м

 м>b1
м>b1
Принимаем  м
м
Приведенная высота сжатого пояса (плиты):

Нижнее уширение балки:
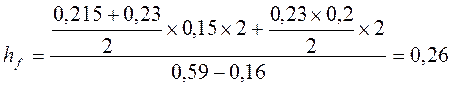 м
м
Площадь поперечного сечения балки:
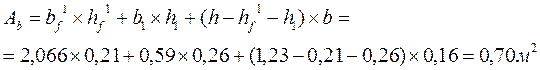
Нормативный вес балки: 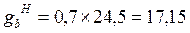 кН/м;
кН/м;
Расчётный вес балки:  кН/м
кН/м
Постоянная нагрузка на 1 пог. метр балки равна:
- нормативная - 
- расчётная - 
2.2 Поперечное распределение временных нагрузок.
Временная нагрузка может занимать различное положение по ширине моста. Для расчета одной из балок пролетного строения необходимо временную нагрузку установить в положение, обеспечивающее наибольшее значение расчетных усилий. Поперечное распределение временной нагрузки характеризуется коэффициентом поперечной установки (К), который определяет долю временной нагрузки, приходящейся на рассматриваемую балку. Коэффициенты К в зависимости от длины и конструкции поперечного сечения пролетного строения определяются различными способами. В курсовой работе К можно определить по методу внецентрального сжатия. Для одинаковых поперек моста балок строим линии влияния давления на крайнюю балку (рис. 14):


где: n – число главных балок поперек моста;
аi – расстояние между симметрично расположенными балками
аmax – расстояние между крайними балками.
По методу внецентренного сжатия самыми нагруженными балками являются крайние. Линии влияния давления загружаем временной нагрузкой невыгодным способом. Если принять за единицу давления оси (одной полосы), то коэффициент поперечной установки 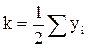 , где
, где
yi – ордината линии влияния под грузами.
При расчетах на прочность и устойчивость следует рассматривать две схемы установки нагрузки АК поперек моста: первая – нагрузка АК устанавливается в невыгодное положение в пределах проезжей части (без учета полос безопасности). Число полос нагрузки равно числу полос движения; вторая – нагрузка АК – (две полосы для габаритов Г-8, Г-10, и Г-11.5) устанавливается в невыгодное положение на всей ширине моста с учетом полос безопасности.
Оси крайних полос нагрузки АК должны быть не ближе 0.55 от кромки проезжей части при первой схеме загружения и от кромки ограждения ездового полотна при второй схеме. При определении усилий по второй схеме загружения не учитывается нагрузка от «толпы» на тротуарах. При расчете по второй группе предельных состояний учитывается только первая схема загружения. Нагрузку НК-100 устанавливают на проезжей части моста вдоль направления движения и не учитывается совместно с нагрузкой на тротуарах и при расчетах на трещиностойкость. При определении усилий от двух и более полос нагрузки АК нагрузки от первой наиболее неблагоприятной полосы загружения вводится в расчет с коэффициентом S1=1.0 остальные- с коэффициентом S1=0.6. Для нагрузки от тележки на всех полосах нагрузок S1=1.0.

Рисунок 7 – Расчётная схемы загружения
Вычисление коэффициентов поперечной установки.

 ;
; 

1. А14+толпа на тротуарах

 =0,19
=0,19
 =0.17
=0.17
2. А14+max к ограждению безопасности


3.Загружение нагрузкой НК-100:

2.3 Расчёт изгибающих моментов и поперечных сил
Постоянные нагрузки определяются:
 ;
;

 ;
;

где  – коэффиценты надежности
– коэффиценты надежности
ω – площадь линии влияния
Усилия в характерных сечениях балки определяются для каждого сечения временных нагрузок для I и II групп предельных состояний.
Сочетание I:
 ;
;
Сочетание II:
 ;
;
Сочетание III:
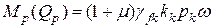 ;
;
Коэффициенты надежности:
 ;
;  при λ=0;
при λ=0; 
 ;
;  при
при  м; для
м; для 

Динамический коэффициент для нагрузки АК:

λ – длина загружения
Нагрузка НК-100 1+μ=1,30 при 
1+μ=1,10 при 
V=14 кН/м; P=140 кН
Рк – эквивалентная нагрузка, определяется по табл. 4;
ω – площадь линии влияния;
Рт =3,92-0,0196λ кПа; λ – длина загружения 16,3м
PT = 3,60 кПа

0 – опорное
 Сечение 1 – на расстоянии 1.5 м
Сечение 1 – на расстоянии 1.5 м
от опоры
Сечение 2 – четверть пролета
Сечении 3 – середина пролета
M – моменты
Сечение 3:
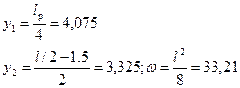
Сечение 2:

Сечение 1:

Q – силы
Сечение 3:

Сечение 2:

Сечение 1:

Сечение 0:

Рисунок 8 – Линии влияния М и Q в расчётных сечениях.
Таблица 2
| № сеч-ния | Площадь линии влияния | Ординаты линий влияния по грузам Р | Коэффициенты поперечной нагрузки | ||||||||||||
| М | Q | М | Q | А14+нагрузка на тротуар | А14 | НК-100 Kk | |||||||||
| + | - | y1 | y2 | y1 | y2 | Kν | Kp | Kт | Kν | Kp | |||||
| - | 8,15 | - | - | - | 1,0 | 0,94 | 0,121 | 0,19 | 0,17 | 0,4517 | 0,4895 | 0,215 | |||
| 11,1 | 6,72 | 0,048 | 1,36 | 1,22 | 0,91 | 0,82 | - | - | - | - | - | - | |||
| 24,9 | 4,58 | 0,51 | 3,06 | 2,68 | 0,75 | 0,66 | - | - | - | - | - | - | |||
| 33,21 | 2,04 | 2,92 | 4,075 | 3,325 | 0,5 | 0,4 | - | - | - | - | - | - | |||
Сечение 0-0:
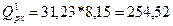 кН
кН 
 кН
кН
 кН
кН
 кН
кН
 кН
кН
 кН
кН
Сечение 1-1:
 кН
кН
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
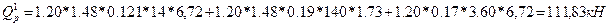
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
Сечение 2-2:
 кН
кН
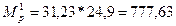 кН*м
кН*м
 кН
кН
 кН*м
кН*м

 кН*м
кН*м
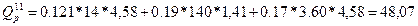 кН
кН
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
Сечение 3-3:

 кН*м
кН*м
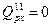
 кН*м
кН*м

 кН*м
кН*м
 кН
кН
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
 кН
кН
 кН*м
кН*м
Таблица 3 Расчетные усилия и моменты от постоянных моментов временных нагрузок
| № сече-ний | Постоянные нагрузки | Временные наргузки, | Максимальные расчетные усилия | |||||||||||||
| I группа предельных состояний | II группа предельных состояний | А14 + нагрузка на тротуар | А11 | НК-100 | ||||||||||||
| Mg кНм | Qg кН | MgH кНм | QgH кН | I группа пред. состояний | II группа пред. состояний | Mp кНм | Qp кН | Mp кНм | Qp кН | I группа пред. состояний | II группа пред. состояний | |||||
| Mp | Qp | MpH | QpH | M | Q | M | Q | |||||||||
| - | 254,52 | - | 242,14 | - | 123,06 | - | 70,4 | - | 341,0 | - | 278,08 | - | 595,52 | - | 312,54 | |
| 346,65 | 208,37 | 198,23 | 329,78 | 163,42 | 111,83 | 94,22 | 61,51 | 438,86 | 286,16 | 378,74 | 229,29 | 785,51 | 494,53 | 292,45 | 391,29 | |
| 777,63 | 127,11 | 739,78 | 120,92 | 351,61 | 83,74 | 202,92 | 48,07 | 945,80 | 223,16 | 813,95 | 149,71 | 1723,43 | 350,27 | 942,7 | 168,99 | |
| 1037,14 | - | 986,67 | - | 473,88 | 50,15 | 273,42 | 28,69 | 1274,18 | 132,52 | 1085,59 | 66,68 | 2347,32 | 132,52 | 1260,09 | 28,69 |
3.Расчет предварительно-напряженных балок по двух группам предельных состояний
3.1 Расчет балки на прочность по нормальному сечению

Рисунок9 – Армирование балки напрягаемой арматурой
Расчетный изгибающий момент в сечении 3 (середина пролета) (см.табл 3):
 кН*м
кН*м
Принимаем 9 пучков напрягаемой арматуры класса К-7, диаметр каната 12 мм.
Положение центра тяжести напрягаемой арматуры:
 м;
м;
Рабочая высота сечения:  м;
м;
Необходимую площадь напрягаемой арматуры определяем по формуле:
 ;
;
Rр = 1055 мПа – расчетное сопротивление на растяжение высокопрочной проволоки диаметром 12 мм, арматурных канатов К-7.
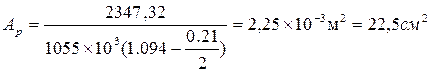
Количество проволок в каждом пучке:
 (3 проволоки)
(3 проволоки)
0,906 – площадь сечения одной проволоки в см2.
Действительная площадь напрягаемой арматуры:
Ар=9х3х0.906=24,46(см2)
Сечение 2:
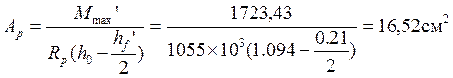
Количество пучков в сечении 2:
 (7 пучков)
(7 пучков)
Сечение 1:

Количество пучков в сечении 1:
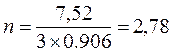 (3 пучка).
(3 пучка).
Проверка:
Определяем границу сжатой зоны сечения:





Условие прочности:


2347,32<2760,46
Условие прочности выполняется.
3.2. Расчет прочности наклонного сечения

Рисунок 10 – Расчётная схема.

 – усилие воспринимаемое хомутами;
– усилие воспринимаемое хомутами;
 - коэффициент условия работы для стержневой арматуры;
- коэффициент условия работы для стержневой арматуры;
 - для напрягаемых пучков;
- для напрягаемых пучков;
 – усилие воспринимаемое отогнутой арматурой;
– усилие воспринимаемое отогнутой арматурой;
 ;
;
С – длина проекции наклонного сечения;
 м;
м;
 м;
м;
 м;
м;
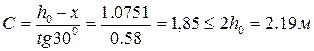 ;
;

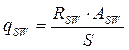 ;
;
 – поперечное усилие, восприимаемое бетоном сжатой зоны сечения.
– поперечное усилие, восприимаемое бетоном сжатой зоны сечения.
 ;
;
 – коэффициент условия работы,
– коэффициент условия работы,  .
.
3.3. Расчет наклонных сечений на действие поперечных сил
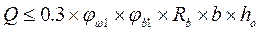
Q=494,53 кН – максимальная поперечная сила в сечении 1
(см.таблицу 3)
 ;
;
ES = 2.06х105 – модуль упругости стали A-II;
Eb = 36,0х103 – модуль упругости бетона класса В35;
b = 0,26м – ширина ребра (стенки) на опоре;
SW = 0,15м – расстояние между хомутами, что меньше 0,41м;
SW ≤ Н/3 = 1,23/3 = 0,41м
АW – площадь сечения ветвей хомутов, расположенных в одной плоскости.
Задаемся диаметром хомутов 10 мм.
 м2;
м2;
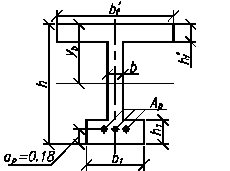
 ;
;
 ;
;

0,3х2,73х0,78х22х103х0,26х1,094=3997,5 кН
3997,5 > 494,53 – условие прочности выполняется.
3.4. Расчет поперечного армирования балки
 кН
кН
1,30х1,40х103х0,26х1,094=517,68>470,97 кН;
Qb = 470,97кН < Q = 494,53 кН
QSW = m04·qSW·c - усилие воспринимаемое поперечной арматуры;

Принимаем наименьшее значение "с":
с = h0 = 109,4 см
QSW = 0,8*5,09*109,4 = 445кН
Qb + QSW = 470,97+445=915,97кН, что больше Q = 494,53кН
Прочность наклонного сечения обеспечена без устройства отгибов
3.5 Определение геометрических характеристик приведённого сечения балки
Геометрические характеристики вычисляют с учетом стадийности работы балок.
Балки с натяжением до бетонирования (стендового изготовления) работают в одну стадию.
Балки с натяжением на бетон работают в две стадии: первая стадия – работает балка ослабленная каналами (стадия изготовления); вторая стадия – работает балка с приведенной площадью сечения (стадия эксплуатации).
Балка с натяжением на упоры (стендовое изготовление).
 Середина пролета:
Середина пролета:
 ;
;  ;
;  ;
;
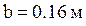 ;
;
 ;
;  ;
;  .
.
Площадь приведенного сечения:
 ;
;

Статический момент сечения относительно нижней грани сечения балки:

Расстояние от низа балки до центра тяжести сечения:
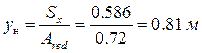 ;
;
 ;
;
Момент инерции приведенного сечения относительно оси проходящей через центр тяжести сечения:
 ;
;

Сечение на расстоянии h = 1.50 от опорного сечения.



 3.6. Определение потерь предварительного напряжения в арматуре
3.6. Определение потерь предварительного напряжения в арматуре
Напряжение в элементах предварительно напряженных конструкций следует принимать по контролируемому усилию за вычетом:
первых потерь – на стадии обжатия бетона,
первых и вторых – на стадии эксплуатации.
Первые потери: а) в конструкциях с натяжением на упоры: от деформации анкеров, трения об огибающие устройства, 50% потерь от релаксации напряжений в арматуре, температурный перепад, быстронатекающая ползучесть, от деформации форм.
б) в конструкциях с натяжением на бетон – от деформации анкеров, трения арматуры о стенки канала, 50% потерь от релаксации напряжений в арматуре.
Вторые потери: а) натяжение на упоры – от усадки и ползучести бетона, 50% потерь от релаксации напряжений в арматуре.
б) натяжение на бетон – от усадки и ползучести, 50% потерь от релаксации, от деформации стыков между блоками в составных по длине конструкциях.
Суммарное значение первых и вторых потерь должно быть не менее 100 МПа.
Вычисление потерь предварительного напряжения арматуры
1. Потери от релаксации напряжений в арматуре:
 ;
;
σр – контролируемое напряжение.
L = 16.3 м σp = 990 МПа
Rpn = 1335 МПа – нормативное сопротивление растяжению
 62,51МПа
62,51МПа
2. Натяжение на бетон:
σ2= 0
3. Потери от деформации анкеров:

 мм на каждый анкер
мм на каждый анкер
 21,45МПа
21,45МПа
4. Трения о стенки канала:

5. От деформации стальных форм:
 30МПа
30МПа
6. Быстронатекающая ползучесть
 , при интенсивном твердении бетона
, при интенсивном твердении бетона

 при
при 
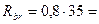 28 МПа
28 МПа
 65,21+0+21,45+0+30=116,66 МПа
65,21+0+21,45+0+30=116,66 МПа
е=  1,487-0,078=1,409
1,487-0,078=1,409
 - нормативный изгибающий момент от собственного веса балки
- нормативный изгибающий момент от собственного веса балки
 0,952.24,5. 68,44=1596,29 кН м
0,952.24,5. 68,44=1596,29 кН м

 0,27< 0,8 - при интенсивном твердении
0,27< 0,8 - при интенсивном твердении
 10,8 Мпа
10,8 Мпа
Для бетонов, подверженных тепловой обработке
 9,18 МПа
9,18 МПа
7.Усадка бетона при натяжении
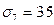 МПа
МПа
8. Ползучесть бетона
 при
при 
 при
при 
 с тепловой обработкой
с тепловой обработкой
 116,66+9,18=125,84 МПа
116,66+9,18=125,84 МПа
 -7,2 МПа
-7,2 МПа

 33,15 МПа
33,15 МПа
9. Смят