Cаратовский государственный технический университет
Измерение длины световой волны с помощью
Дифракционной решетки
Методические указания
к выполнению лабораторной работы по физике
для студентов всех специальностей
всех форм обучения
Электронное издание локального распространения
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
САРАТОВ - 2011
Все права на размножение и распространение в любой форме остаются за разработчиком.
Нелегальное копирование и использование данного продукта запрещено.
Составители – В.Б. Сиволобов, Л.Я. Рихтер.
Под редакцией В.В. Сысоева.
Рецензент – И.В. Беляев
410054, Саратов, ул. Политехническая 77,
Научно-техническая библиотека СГТУ,
тел. 52-63-81, 52-56-01
https://lib.sstu.ru
Регистрационный
номер
© Саратовский государственный
технический университет 2011 г.
ЦЕЛЬ РАБОТЫ: определить длину световой волны с помощью дифракционной решетки
ОСНОВНЫЕ ПОНЯТИЯ
Дифракцией света называется явление отступления от законов прямолинейного распространения света, обусловленное его волновой природой. Дифракция приводит, в частности, к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Особенно заметно дифракция проявляется, когда размеры препятствий соизмеримы с длиной световой волны. В результате дифракции за препятствием наблюдается дифракционная картина – светлые и темные полосы, кольца и т.д., в зависимости от формы препятствия.
Дифракционная картина является результатом сложения (интерференции) так называемых вторичных световых волн. Понятие о вторичных световых волнах было введено Гюйгенсом. Затем его идеи были развиты Френелем, который учел сложение вторичных световых волн.
Назовем фронтом световой волны поверхность в пространстве, до которой в данный момент дошли световые колебания в одной фазе. Световые лучи в изотропной среде всегда перпендикулярны фронту световой волны. Например, точечный источник света создает сферический фронт волны, а лучи расходятся по радиусам.
Согласно принципу Гюйгенса каждую точку фронта световой волны можно рассматривать как самостоятельный источник сферических световых волн. Эти волны называются вторичными. В любой следующий момент времени фронт волны можно построить как поверхность, огибающую все вторичные волны.
Вторичные волны складываются друг с другом и могут в одних точках пространства взаимно усилить друг друга, а в других – взаимно ослабить или совсем погасить.
Принцип Гюйгенса – Френеля формулируется следующим образом: амплитуда световой волны в любой точке пространства определяется сложением вторичных волн, которые приходят в эту точку от всех отдельных частей фронта световой волны.
ДИФРАКЦИЯ НА УЗКОЙ ЩЕЛИ
Воспользуемся принципом Гюйгенса – Френеля в частном случае дифракции на одной узкой щели. Пусть параллельный пучок лучей падает нормально на непрозрачный экран, в котором имеется щель. Параллельному пучку лучей соответствует плоский фронт световой волны.
Согласно принципу Гюйгенса каждая точка фронта волны в щели является источником вторичных сферических волн и посылает лучи во всех возможных направлениях (Рис. 1a). Поставим на пути лучей собирающую линзу и в ее фокальной плоскости поместим экран (Рис. 1b). В каждой точке этого экрана будут складываться вторичные волны от щели, прошедшие линзу, и на экране возникает дифракционная картина.
Вторичные волны падают на линзу под всевозможными углами. Выделим лучи, составляющие произвольный угол φ с первоначальным направлением. Линза соберет эти лучи в определенной точке М фокальной плоскости и все эти лучи в данной точке проинтерферируют.
Чтобы определить результат интерференции воспользуемся методом зон Френеля. Зонами Френеля называют такие участки фронта первичной волны, что вторичные волны от них, складываясь, взаимно гасят друг друга.
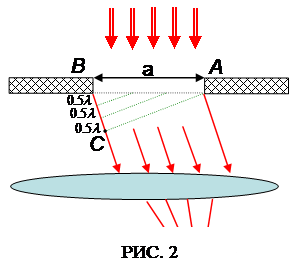
Разобьем фронт световой волны в щели на зоны Френеля, согласно Рис. 2. Пусть а – ширина щели, из которой выходит пучок света. Опустим из точки А перпендикуляр АС на крайний луч выделенного пучка. Разделим мысленно линию ВС = аsinφ на ряд отрезков длиной 
. Проводя из концов этих отрезков линии, параллельные АС, до их пересечения с АВ, мы разобьем фронт волны в щели на ряд полосок одинаковой ширины 1,2,3 и т.д. Эти полоски и являются зонами Френеля.
Совместное действие вторичных волн от двух соседних зон Френеля в точке М приводит к их взаимному гашению, так как волны от соответствующих участков соседних зон (например, от крайних левых, средних и т.д.) приходят в точку М со сдвигом на . Следовательно, если данному углу наклона φ соответствует четное число зон Френеля, то в точке М, в которой соберутся эти лучи, наблюдается минимум интенсивности. Если число зон окажется нечетным, то одна зона останется некомпенсированной, и в точке М наблюдается максимум интенсивности.
В большинстве случаев число зон Френеля не будет целым числом. Для таких углов наблюдается некоторая промежуточная интенсивность.
Выразим условие максимума и минимума интенсивности в общем виде. Из Рис. 2 видно, что число зон Френеля равно
.
Причем число зон может быть как целым, так и дробным.
В точках максимума число Z должно быть целым нечетным, а в точках минимума – целым четным. Возьмем целое число, не равное нулю k=1,2,3,… Любое число 2k будет четным, а (2k+1) – нечетным числом. 
Тогда в точках максимума
,
откуда
.
В точках минимума
,
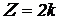откуда
.
В центре экрана, которому соответствует угол φ=0, наблюдается центральный максимум, так как все вторичные волны приходят в центр в одинаковой фазе.
В целом дифракционная картина представляет собой центральную светлую полосу, параллельную щели, интенсивность которой убывает к краям, а по обе стороны расположены чередующиеся темные и светлые полосы. Распределение интенсивности вдоль экрана изображено на Рис. 3.
ДИФРАКЦИОННАЯ РЕШЕТКА
Дифракционная решетка предназначается для разложения света сложного состава и спектр по длинам волн. Она представляет собой ряд прозрачных щелей одинаковой ширины а, разделенных непрозрачными промежутками шириной b.
Чтобы изготовить решетку, на стеклянную пластинку алмазным резцом с помощью делительной машины наносят ряд параллельных штрихов. Штрихи являются непрозрачными промежутками, а неповрежденные места между ними – прозрачными щелями. 
На каждый миллиметр длины решетки наносятся от 100 до 1200 штрихов, а всего решетка может содержать более 100000 штрихов и, значит, такое же количество щелей.
Периодом дифракционной решетки (или постоянной решетки) d называется сумма ширины щели а и непрозрачного промежутка b (Рис. 4).
УСЛОВИЕ ГЛАВНОГО МАКСИМУМА
Так же как и в случае одной щели, на решетку направляют параллельный пучок лучей, устанавливают линзу и экран в ее фокальной плоскости (Рис. 5).
На щелях решетки происходит дифракция света. Каждая щель является источником вторичных волн. Лучи расходятся из каждой щели по всевозможным направлениям. Собранные линзой лучи (вторичные волны) интерферируют в плоскости экрана.
Дифракционная картина, создаваемая решеткой, существенно отличается от дифракционной картины, создаваемой одной щелью. Характерным отличием дифракционной картины от решетки является наличие узких и ярких главных максимумов, в которых сосредоточена практически вся энергия.
Найдем условие главного максимума. Выделим пучки, идущие из щелей под произвольным углом φ к первоначальному направлению (Рис. 5). Чтобы пучки при сложении максимально усилили друг друга, нужно, чтобы разность хода ∆ между ними, то есть разность расстояний, которые пройдут эти пучки до точки сложения, равнялась целому числу длин волн. Иначе говоря, 
, где k – целое число.
Из Рис. 5 видно, что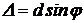 
, откуда условие главного максимума можно записать как
,
где целое число k =0, ±1, ±2, … называется порядком максимума. Так может быть максимум нулевого порядка, первого порядка и т.д.
Теория интерференции многих пучков показывает, что при очень большом числе щелей в решетке, экран между главными максимумами практически весь будет темным, так что никаких «минимумов» от реальной решетки не наблюдается. Во всех точках, где не выполняется условие главного максимума, вторичные волны при сложении практически гасят друг друга.
Если осветить решетку монохроматическим светом, то есть светом с определенной длиной волны, то на экране будут наблюдаться узкие светлые полосы на темном фоне (Рис. 6).
РИС. 6
Цвет полос определяется длиной волны света. Центральная полоса (полоса нулевого порядка) соответствует k =0.
Максимальное число наблюдаемых полос определяется из условия 
, то есть 
и 
ДИФРАКЦИОННЫЙ СПЕКТР
Условие главного максимума можно переписать в виде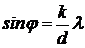 
.
Пусть в центре экрана, т. О, начало отсчета. Положение главного максимума на экране (т. М) определяется расстоянием 
от т. О (Рис. 7). Если обозначить как f – фокусное расстояние линзы, то из Рис. 7 видно, что
.
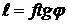При малых углах 
. Тогда для малых углов, учитывая условие главного максимума, получим
.
Как видно, для данного порядка k расстояние максимума от центра экрана пропорционально длине волны света.
Если решетку осветить белым светом, который представляет собой совокупность всевозможных длин волн, то положения главных максимумов на экране для различных длин волн не совпадут. Свет разложится в спектр, обращенный фиолетовым концом к центру экрана, так как фиолетовый свет имеет меньшую длину волны (
нм) по сравнению с длиной волны красного света (
нм). При разложении белого света главные максимумы на экране для различных длин волн примыкают друг к другу и цвета спектра непрерывно переходят один в другой. Одновременно на экране наблюдается несколько спектров различных порядков (Рис. 8).
В центре экрана (
) наблюдается спектр нулевого порядка, не разложенный по длинам волн, то есть белая полоса. При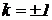 
наблюдается симметрично расположенные спектры первого порядка. При k = ±2, ±3,… наблюдаются спектры второго и более высоких порядков. Таким образом, дифракционные спектры возникают в результате интерференции на экране вторичных волн от щелей решетки. Вторичные волны любого цвета приходят во все точки экрана, но взаимно гасятся везде, кроме тех мест, где выполняется условие главного максимума.
ОПРЕДЕЛЕНИЕ ДЛИНЫСВЕТОВОЙ ВОЛНЫПО ДИФРАКЦИОННОМУ СПЕКТРУ
Схема установки изображена на Рис. 9. На рисунке сделаны следующие обозначения: 1 – осветитель; 2 – диск с цветными светофильтрами; 3 – щель, прорезанная в черном экране, на фоне которого наблюдаются спектры; 4 – миллиметровая шкала; 5 – дифракционная решетка с периодом d = 0,01 мм; 6 – отверстие, через которое ведется наблюдение.
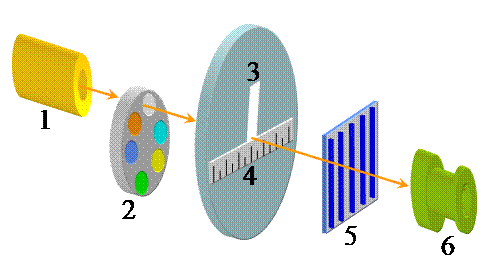
Глаз наблюдателя располагается непосредственно за дифракционной решеткой. Линзой служит оптическая система глаза, а экраном – сетчатка. Дифракционный спектр образуется на сетчатке глаза, но наблюдатель его видит на фоне темного экрана в непосредственной близости от миллиметровой шкалы.
На Рис. 10 один из главных максимумов образовался в точке М на сетчатке. Наблюдатель его видит в точке М’ на темном экране на расстоянии 
от нулевого максимума (щели).
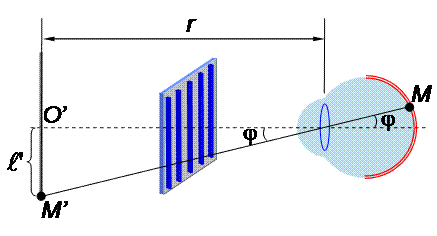
Из условия главного максимума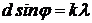 
можно выразить длину волны
.
Как уже отмечалось, при малых углах 
. Из Рис. 10 видно, что
,
где r – расстояние от глаза наблюдателя до экрана. Таким образом, получим формулу для определения длины волны
,
которая является рабочей в данной лабораторной работе.
Так как глаз наблюдателя расположен близко к дифракционной решетке, то расстояние r можно измерить от решетки до экрана.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Фотография экспериментальной установки представлена на Рис. 11. Цифры соответствуют обозначениям, использованным на Рис. 9.
Измерения проводят в следующем порядке. Включают осветитель, устанавливают против щели бесцветный фильтр, экран со щелью передвигают на расстояние r, которое задается преподавателем. На экране должны быть видны яркие непрерывные спектры первого и второго порядка.
Чтобы найти длину волны определенного цвета необходимо найти расстояние 
положения максимума этого цвета от центра экрана. Для этого предлагается определить расстояние между полосками одного цвета первого и второго порядка 
и 
(см. Рис. 12).
РИС. 11
РИС. 12
В этом случае для линий первого порядка получаем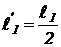 
, для линий второго порядка 
. После этого, используя рабочую формулу, рассчитывают длину волны соответствующего цвета 
и 
. Период дифракционной решетки, используемой в данной лабораторной работе, d=10 мкм. Окончательно, среднее значение длины волны будет 
.
Определение длин волн производят для различных цветов, например, красного, синего и зеленого (по заданию преподавателя).
Затем устанавливают цветные светофильтры, соответствующие тем же заданным цветам и повторяют измерения, сравнивая значения, полученные при применении бесцветного и цветного светофильтров.
В отчете по работе должны быть указаны цвет заданного светофильтра, заданное значение r, все отсчеты с письменным объяснением значений всех чисел, рабочие формулы с подставленными числами, вычисленные значения длин волн и их средние значения.
ВОПРОСЫК ОТЧЕТУ
1. Что такое свет с точки зрения электромагнитной теории?
2. В чем заключается явление дифракции света?
3. Сформулируйте и объясните принцип Гюйгенса-Френеля.
4. Объясните явление дифракции на узкой щели.
5. Что такое дифракционная решетка? Объясните явление дифракции в дифракционной решетке.
6. Объясните разложение белого света в спектр с помощью дифракционной решетки.
7. Как определить длину волны с помощью дифракционной решетки? Поясните рабочую формулу.
ЛИТЕРАТУРА
1. Гольдин Л. Д. Руководство к лабораторным занятиям по физике / Л. Д. Гольдин.- М.: Наука. Любой год издания.
2. Грибов Л. А. Основы физики / Л. А. Грибов, Н. И. Прокофьева.- М.: Градарика, 1998.
3. Детлаф А. А. Курс физики / А. А. Детлаф, В. М. Яворский.- М.: Высшая школа, 1989.
4. Евсеева Л. А. Методические указания к оформлению отчетов по лабораторным работам по физике. / Л. А. Евсеева.- Сарат. гос. техн. ун-т. - Саратов: СГТУ, 1985.
5. Савельев И. В. Курс общей физики, т. 2. / И. В. Савельев.- М.: Наука, Гл. ред. физ.-мат. лит. Любой год издания.
6. Трофимова Т. И. Курс физики. / Т. И. Трофимова.- М.: Высшая школа, 2002.