Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки А, С и М, где М – середина ребра A1D1.
 сечение - это трапеция АМКС.
сечение - это трапеция АМКС.
7. Определение. Две плоскости называются параллельными, если они не имеют общих точек.
Параллельность плоскостей и обозначается так: ||. Рассмотрим признак параллельности двух плоскостей.

Свойства параллельных плоскостей:
1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
2. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
Перпендикулярные прямые в пространстве
Две прямые называются перпендикулярными, если угол между ними равен 90°.
В пространстве перпендикулярными называют не только пересекающиеся прямые, но и скрещивающиеся прямые, так как мы говорим об угле, который могут образовать эти прямые, если их поместить в одной плоскости.
Так же как и в плоскости, в пространстве перпендикулярные прямые a и b обозначают a⊥b.
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая перпендикулярна к этой прямой.
Перпендикулярность прямой и плоскости
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости.
Перпендикулярность прямой и плоскости обозначается как a⊥α.
Через любую точку пространства проходит прямая перпендикулярно данной плоскости, притом только одна.
Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна этой плоскости.
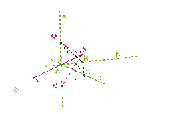
Доказательство:
Пусть a — прямая, перпендикулярная прямым b и c в плоскости. Проведём прямую a через точку Aпересечения прямых b и c. Докажем, что прямая a перпендикулярна плоскости, то есть каждой прямой в этой плоскости.
1. Проведём произвольную прямую x через точку A в плоскости и покажем, что она перпендикулярна прямой a. Проведём в плоскости произвольную прямую, не проходящую через точку A и пересекающую прямые b, c и x. Пусть точками пересечения будут B, C и X.
2. Отложим на прямой a от точки A в разные стороны равные отрезки AM и AN.
3. Треугольник MCN равнобедренный, так как отрезок AC является высотой по условию теоремы и медианой по построению (AM=AN). По той же причине треугольник MBN тоже равнобедренный.
4. Следовательно, треугольники MBC и NBC равны по трём сторонам.
5. Из равенства треугольников MBC и NBC следует равенство углов MBX и NBX и, следовательно, равенство треугольников MBX и NBX по двум сторонам и углу между ними.
6. Из равенства сторон MX и NX этих треугольников заключаем, что треугольник MXN равнобедренный. Поэтому его медиана XA является также высотой. А это и значит, что прямая x перпендикулярна a. По определению прямая a перпендикулярна плоскости.
Свойства перпендикулярных прямой и плоскости.
1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
2. Две прямые, перпендикулярные одной и той же плоскости, параллельны.