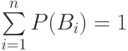Определение вероятности
Пример решения задачи
Вероятностью события называется численная мера степени объективной возможности этого события. Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению события А, к числу n всех несовместных равновозможных элементарных исходов, образующих полную группу событий:
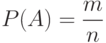
где m – число исходов, n – число всех несовместных равновозможных элементарных исходов.
Из определения следует, что вероятность удовлетворяет условиям
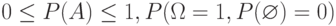
Классическое определение вероятности применяется только в следующих случаях:
1. Число элементарных исходов конечно;
2. Результаты всех испытаний и наблюдений равновозможны;
3. Все равновозможные события образуют полную группу попарно несовместных событий.
Задача: Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?
| Дано: m=120 n=1500 | |
P(A)=?
Решение:
А – купленный билет оказался выигрышным
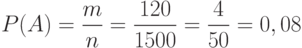
Ответ: P(A)=0.08 или 8%.
Теорема 1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий (ключевое слово "или"):
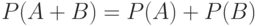
|
Теорема 2. Сумма вероятностей полной группы событий равна единице:
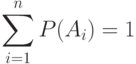
|
Теорема 3. Сумма вероятностей противоположных событий равна единице:
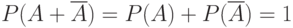
| |||
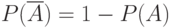
| |||
Теорема 4. Если событие А влечет за собой событие B, т.е.  то
то

|
Теорема 5. Вероятность суммы двух совместных событий вычисляется по формуле:

|
Теорема 6. Вероятность совместного появления событий А и В равна произведению вероятности одного события на условную вероятность другого при условии, что первое событие произошло (ключевое слово "и"), и находится по формуле:
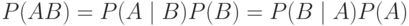
|
Теорема 7. Вероятность произведения независимых событий А и В равна произведению их вероятностей:
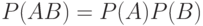
|
Задача: Вероятность появления бракованной детали в партии равна 0,015. Найти вероятность того, что из этой партии будет изъята небракованная деталь.
| Дано: P(A)=0,015 | ||||
| P(B)=? | ||||
Решение: А – деталь, изъятая из партии, бракованная
В – из партии изъята небракованная деталь
По теореме о вероятности противоположного события:
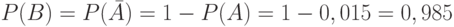 Ответ: P(B)=0,985
Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также в Вероятность события А, которое может наступить при условии появления одного из n несовместных событий (гипотез)
Ответ: P(B)=0,985
Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также в Вероятность события А, которое может наступить при условии появления одного из n несовместных событий (гипотез) 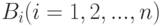 образующих полную группу, находят по формуле полной вероятности: образующих полную группу, находят по формуле полной вероятности:
где P(A) – вероятность события А;
– сумма произведений вероятностей каждого из событий на соответствующую условную вероятность Сумма вероятностей гипотез | ||||
Задача: Из 40 деталей 10 изготовлены в первом цехе, 25 - во втором, а остальные - в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех - с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Дано:
P(A)=0,015
P(B)=?
Решение 1. А – выбрана деталь отличного качества
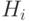 – выбранная деталь изготовлена в i цехе
– выбранная деталь изготовлена в i цехе
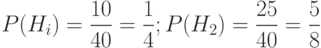
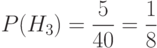
2. По условию задачи
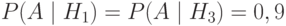

3. По формуле полной вероятности находим искомую вероятность:
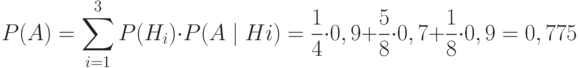
Ответ: P(A)=0,775
Формула Байеса. Вероятность оценки гипотез
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) 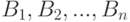 которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
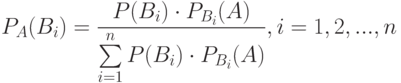
| (1.18) |
где 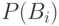 – вероятность события
– вероятность события 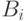 ,
, 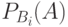 – условная вероятность события А, вычисленная при условии, что событие
– условная вероятность события А, вычисленная при условии, что событие 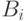 наступило;
наступило; 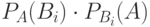 – вероятность события A;
– вероятность события A; 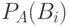 – условная вероятность события
– условная вероятность события 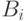 вычисленная при условии, что событие А произошло.
вычисленная при условии, что событие А произошло.
Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Задача: Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что его проверил второй товаровед.
Дано:
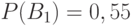
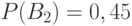
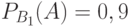
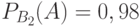
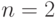
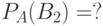
Решение:
1. 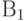 – изделие проверил первый товаровед
– изделие проверил первый товаровед
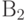 – изделие проверил первый товаровед
– изделие проверил первый товаровед
А – стандартное изделие при проверке признано стандартным
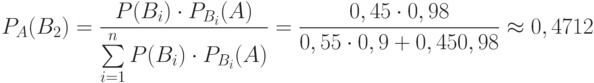
Ответ: 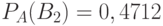
Формула Бернулли
Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна p, то вероятность того, что событие А появится в этих n испытаниях m раз, выражается формулой Бернулли:
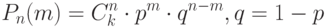
| (1.19) |
где p – вероятность "успеха", q – вероятность "неудачи", m – число исходов, n – число независимых испытаний.
Число  называется наивероятнейшим числом наступлений события А в n испытаниях и равно целой части числа
называется наивероятнейшим числом наступлений события А в n испытаниях и равно целой части числа 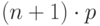 , а при целом
, а при целом 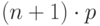 наибольшее значение достигается при двух числах:
наибольшее значение достигается при двух числах: 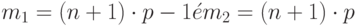
Если  то число
то число  можно определить из двойного неравенства:
можно определить из двойного неравенства:

| (1.20) |
Задача: Игральная кость брошена 6 раз. Найти вероятность того, что ровно 3 раза выпадет "шестерка".
Дано:
m=3
n=6

Решение:
1. Найдем вероятность "успеха":
 (один исход из 6 возможных), тогда
(один исход из 6 возможных), тогда
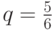 - вероятность "неудачи"
- вероятность "неудачи"
2. Вычисляем вероятность:
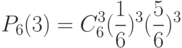
Ответ: 
Формула Пуассона Если вероятность p наступления события A в каждом испытании постоянна и мала, а число независимых испытаний n достаточно велико, то вероятность наступления события A ровно m раз приближенно равна:
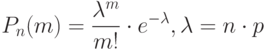
| (1.21) |
где m – число исходов, n – число независимых испытаний, p – вероятность.
Задача: На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.
Дано:
n=100000
p=0,0001
m=3 (m=5)

Решение:
1. Находим 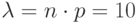
2. Вычисляем вероятность:
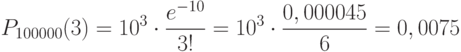
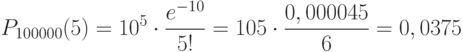
Ответ:
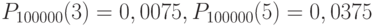
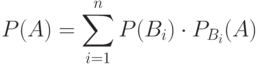
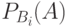 – условная вероятность события А, вычисленная при условии, что событие
– условная вероятность события А, вычисленная при условии, что событие