Теперь приступим к построению языка логики высказываний. Как было указано в главе 1.3., формализованный язык должен содержать три рода символов: содержательные, логические и вспомогательные. В логике высказываний мы оперируем только с высказываниями, поэтому в качестве содержательных, нелогических символов требуются средства для выражения высказываний. Для этой цели обычно используются буквы некоторого фрагмента латинского алфавита: p, q, r и т.д.; они могут снабжаться нижними индексами: p1, p2,… pn. Эти буквы называют пропозициональными (или высказывательными) переменными. Они выражают, или символизируют простые высказывания, и имеют одно из двух истинностных значений. Для обозначения последних удобно ввести ещё два содержательных символа: «И » и «Л ». Их называют пропозициональными константами: буква «И» имеет постоянное значение «истина», буква «Л» имеет постоянное значение «ложь». К логическим символам относятся знаки, обозначающие логические союзы, численность и конкретный выбор которых в разных формализованных языках могут варьироваться. Здесь и далее будет использоваться знак & для обозначения союза «и», знак Ú для обозначения союза «или/и», знак ↮ для обозначения союза «исключающее или», знак É для обозначения союза «если…, то…», знак «для обозначения союза «если и только если…, то…», знак Ø для обозначения союза «не». Наконец, в качестве вспомогательных, технических символов привлекаются скобки. Логические связки могут соединять не только простые, но и сложные высказывания, причём сколь угодно сложные. Поэтому для удобства чтения в одном языке может использоваться более чем один вид скобок. Подытожим сказанное.
|
|
I. Алфавит языка логики высказываний:
– p, q, r..., p1 , q1, r1... символы высказываний (пропозициональные переменные);
– И, Л. собственные имена истины и лжи (пропозициональные константы);
– Ø, &, Ú, ↮, É, ↔, символы логических операций (логические константы);
–), (, ], [ скобки (вспомогательные знаки).
II. Синтаксис языка логики высказываний.
На основе заданного алфавита мы должны описать синтаксис языка, то есть правила построения допустимых выражений из тех символов, которые перечислены в алфавите. Когда синтаксис задан, мы будем в состоянии отличить осмысленные выражения языка от бессмысленных последовательностей символов нашего алфавита. Здесь эта цель достигается всего лишь с помощью одного определения – определения правильно построенного высказывания[2] (сокращенно – ППВ).
Определение ППВ:
1. Пропозициональная переменная или пропозициональная константа есть ППВ.
2. Если и только если А – ППВ, то Ø(А) – тоже ППВ. Ø(ЛØ) Ø p&Øq
3. Если А и В – ППВ, то (А)& (В), (А)Ú (В), (А)É (В),(А)↔ (В), (А)↮ (В) – тоже ППВ.
4. Других ППВ, кроме перечисленных в пунктах 1–3, в языке ЛВ нет.
Обратим внимание, что в определении ППВ использованы буквы А и В, которых нет в алфавите нашего языка. Это не что иное, как символы метаязыка (см. глава 1.3.), под которыми следует понимать сокращённое выражение для любой последовательности символов алфавита. Выражения, содержащие такие буквы, называют также схемами высказываний.
Пункт 1 определения позволяет нам получить, например, такие ППВ, как q; r; Л.
|
|
Пункт 1 вместе с пунктом 2 заставляет признать как ППВ Ø q, ØØ q, Ø И. В соответствии с определением, выражение, следующее после каждого знака отрицания, должно заключаться в скобки. В частности, второй пример должен быть записан так: Ø(Ø(q)). Однако в данном случае отсутствие скобок не приводит к двусмысленностям, поэтому здесь, как и в дальнейшем в подобных случаях, избыточные скобки будут опускаться.
Благодаря совместному применению пунктов 1 и 3 мы можем построить ППВ p & q, (p & q)Ú r, p & (q Ú r); (r É p)&(q Ú q1). В последних трёх примерах применение некоторых скобок уже необходимо. Так, без их помощи мы не сможем выразить различие между (p & q)Ú r и p & (q Ú r). В первом случае мы имеем частный случай схемы (А)Ú (В), где А представлено высказыванием (p & q), а В – высказыванием r; в то время как втором случае перед нами пример схемы (А)& (В), где А представлено высказыванием p, а В – высказыванием (q Ú r).
Наконец, используя все три пункта, мы можем построить такие ППВ, как p &Ø q, r ÉØ(p &Ø q), Ø(r É p)&(Ø q Ú q1).
Предлагаем читателю самостоятельно объяснить, по каким причинам следующие последовательности символов не являются ППВ: p Ø, & q, p Ø& q, p(r Ú q)
III. Семантика.
Задача семантики состоит в том, чтобы мы могли устанавливать значение любого выражения языка, удовлетворяющего правилам синтаксиса, или, проще говоря, значение любого ППВ.
Пропозициональные константы представляют собой частный случай имён собственных, и потому обозначают определеные объекты: И обозначает идеальный объект «истина», Л обозначает идеальный объект «ложь». Каждая пропозициональная переменная неопределенным образом обозначает один из двух объектов – истину или ложь. Вспомогательные знаки сами по себе ничего не обозначают, именно поэтому они и называются вспомогательными.
|
|
О знаках, обозначающих логические связки, поговорим подробней.
1. Знак отрицания Ø обозначает логическую связку «не». Ø р может читаться как «не- р » или «неверно, что р ». Если некоторое ППВ А истинно, то Ø А является ложным; если же А ложно, то ØА – истинно. Для определения логических связок принято использовать таблицы истинности. Такая таблица включает в себя, во-первых, входные столбцы, во-вторых, один выходной (или результирующий) столбец. Во входных столбцах перебираются все возможные комбинации истинностных значений простых высказываний, которые связываются определяемым логическим союзом. Иначе говоря, во входных столбцах перечисляются все возможные интерпретации данного набора переменных (см. §1.3). В выходном столбце указываются истинностные значения сложного высказывания, полученного в результате применения соответствующей связки к исходным высказываниям. Поскольку отрицание является унарной связкой, т.е. операцией, осуществляемой над одной переменной, для полного перебора исходных значений достаточно одного входного столбца, а весь перебор займёт две строки (рис.2.1):
| А | Ø А |
| и | л |
| л | и |
Рис. 2.1.
В таблице на рис.2.1 входной столбец расположен слева, выходной – справа. В первой строке представлена интерпретация, на которой А имеет значение истина, соответственно, Ø А на этой интерпретации получает значение ложь. Аналогично во второй строке.
2. Знак конъюнкции & обозначает логический союз «и», с помощью которого образуется соединительное высказывание (его называют и конъюнктивным – по имени связки). Сложное высказывание, образованное с помощью этой связки, истинно тогда и только тогда, когда истинно каждое из составляющих его высказываний.
Поскольку конъюнкция является бинарной связкой, для её табличного определения требуется два входных столбца: по одному для каждой соединяемой переменной. Полный перебор возможных интерпретаций займёт четыре строки. В выходном столбце, представляющем результат выполнения операции, значение «истина» содержится только в строке, представляющей интерпретацию, на которой обе соединяемые переменные, и А, и В, являются истинными. Мы верим, что читатель сможет самостоятельно найти эту строку в таблице на рис. 2.2.
| А | В | А&В |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
Рис 2.2.
Заметим, что знак & не является просто заменителем союза русского языка «и». Во-первых, эта логическая связь может выражаться и другими средствами языка, например, с помощью союзов «а», «но», «не только..., но и...», «несмотря на то что» и т.д., или просто перечислением предложений через запятую. Во-вторых, не всегда союз «и» естественного языка выражает конъюнктивную связь. Например, в предложении «Бологое находится между Петербургом и Москвой» союз «и » не выражает конъюнкции, поскольку здесь нет двух высказываний, из которых с помощью «и» строилось бы сложное высказывание. Более тонким контрпримером может служить такое предложение, как «Он увидел собаку Баскервилей и дико закричал». Здесь с помощью «и » два простых высказывания действительно, соединяются в одно сложное, но это сложное высказывание не будет конъюнктивным. Оно выражает последовательность двух событий во времени, причём между этими событиями явно имеется причинная связь. Ведь если мы поменяем местами входящие в него предложения, то получим «Он дико закричал и увидел собаку Баскервилей», что несомненно будет иметь иной смысл, и, пожалуй, иное истинностное значение.
3. Знак дизъюнкции слабой (её также называют нестрогой и неисключающей) Ú обозначает логический союз «и/или». С помощью этого союза образуется разделительное высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из составляющих его высказываний. В русском языке дизъюнкция обычно выражается союзом «или». Например: для подготовки к семинару, надо прочитать конспект или учебник. Табличное определение этой связки представлено на рис. 2.3.
| А | В | А Ú В |
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
Рис.2.3.
Слабая дизъюнкция будет ложной лишь в том случае, если все входящие в неё простые высказывания являются ложными. Так, высказывание «кенгуру обитают в России или в Бразилии» будет ложным, но «кенгуру обитают в России или в Австралии» - истинным
4. Знак дизъюнкции сильной (или строгой, исключающей) ↮ обозначает логический союз «исключающее или». С его помощью образуется исключающее разделительное высказывание. Это сложное высказывание, которое истинно тогда и только тогда, когда истинно ровно одно из входящих в него высказываний. В русском языке обычно выражается союзом «либо..., либо...». Например: со щитом либо на щите. Его табличное определение представлено на рис. 2.4.
| А | В | А ↮ В |
| и | и | л |
| и | л | и |
| л | и | и |
| л | Л | л |
Рис. 2.4.
Строгая дизъюнкция отличается от слабой тем, что она будет ложной, когда оба входящие в неё высказывания истинны. Так, если в приведенном выше примере простые высказывания «для подготовки к семинару, надо прочитать учебник» и «для подготовки к семинару, надо прочитать конспект» соединить строгой дизъюнкцией, то мы получим сложное высказывание, которое имеет истинностное значение «Ложь». Действительно, поскольку оба связываемых высказывания истинны, ему соответствует первая строка таблицы истинности, в которой строгая дизъюнкция получает значение «ложь». Если же мы соединим их слабой дизъюнкцией, то получим истинное сложное высказывание.
5. Знак эквиваленции «обозначает логический союз «если и только если …, то…», с помощью которого образуется высказывание эквивалентности. Это такое сложное высказывание, которое истинно тогда и только тогда, когда истинностные значения составляющих его высказываний совпадают. Эта связка, выраженная словами «тогда и только тогда, когда», использовалась во всех только что приведенных определениях. Её табличное определение можно найти на рис. 2.5.
| А | В | А ↔ В |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | и |
Рис. 2.5.
Заметим, что все описанные до сих пор связки имеют свойство коммутативности: соединяемые ими высказывания можно менять местами, не вызывая изменения истинностного значения соответствующего сложного высказывания. p & q имеет такое же значение, как q & p, p Ú q – такое же, как q Ú p. Следующая связка не имеет такого свойства.
6. Знак материальной импликации É обозначает логический союз «если..., то...». Он является формализаций условного высказывания. В отличие от введённых выше, это некоммутативная связка, поэтому каждой её части присвоено свое название. В выражении «если А, то В » высказывание, обозначаемое «А », называется антецедентом (или основанием), а высказывание, обозначаемое «В », называется консеквентом (следствием). С помощью материальной импликации образуется такое сложное высказывание, которое ложно тогда и только тогда, когда его антецедент истинен, а консеквент ложен.
| А | В | А É В |
| и | и | и |
| и | л | л |
| л | и | и |
| л | л | и |
Рис. 2.6.
Формализация условного высказывания с помощью материальной импликации заслуживает несколько более подробного обсуждения. Материальной она называется в том смысле, что при такой формализации учитывается только материя связываемых высказываний, т.е. их истинностные значения, и не принимается во внимание смысловая связь между ними. Если этого не учитывать, несколько странным может показаться тот факт, в третьей и четвёртой строках союз «если..., то…» является истинным.
Чтобы показать справедливость такой формализации, возьмём заведомо истинное условное высказывание, например, «Если число делится на 9, то оно делится на 3», и попытаемся верифицировать отдельные строки таблицы истинности, т.е. для каждой строки найти такие числа, которые делают это высказывание истинным. Чтобы верифицировать первую строку, надо указать такое число, для которого истинно, что оно делится на 9, и истинно, что оно делится на 3. Несомненно, что такие числа существуют, поэтому в первой строке выходного столбца мы вправе написать значение «истина». Вторую строку могло бы верифицировать такое число, для которого истинно, что оно делится на 9, но ложно, что оно делится на 3. Таких чисел нет, что и фиксируется значением «ложь» в соответствующей строке выходного столбца. Наконец, числа, соответствующие третьей и четвёртой строкам, конечно же, существуют: есть числа, для которых ложно, что они делятся на 9, но истинно, что ни делятся на 3, и есть числа, для которых ложно и то, что они делятся на 9, и то, что делятся на 3. Но наличие подобных чисел никоим образом не ставит под сомнение справедливость нашего утверждения, что делимость числа на 9 влечёт его делимость на 3.
Тем не менее, не все могут смириться с тем фактом, что к ложному антецеденту можно присоединять любой консеквент, как истинный, так и ложный, и в результате всегда будет получаться истинное условное высказывание. Эта особенность даже стала называться «парадоксом материальной импликации». Другой так называемый парадокс связан с первой и третьей строками, из которых можно сделать вывод, что к истинному консеквенту можно присоединять любой антецедент, хоть истинный, хоть ложный, всегда получая при этом истинное условное высказывание.
Классическим возражением стал пример американского логика С.Клини «если дважды два равно пяти, то луна сделана из зелёного сыра». В этом высказывании ложны и антецедент, и консеквент, поэтому, согласно табличному определению, его следует считать истинным, но это как будто совершенно противоречит здравому смыслу. На это можно заметить, что соединение не связанных по смыслу высказываний сделает абсурдной любую строку таблицы истинности, и не только у импликации. Так, высказывание «В огороде бузина, а в Киеве дядька» тоже можно рассматривать в качестве примера, ставящего под сомнение справедливость предложенной выше формализации соединительного высказывания, поскольку между соединяемыми здесь простыми высказываниями нет никакой смысловой связи, но оно, тем не менее, претендует на истинность.
Вместе с тем стоит отметить, что некоторые виды условных высказываний действительно не могут быть формализованы с помощью материальной импликации. Это, в частности, контрфактуальные высказывания. Так называются высказывания с заведомо ложным антецедентом, в естественном языке они обычно выражаются предложениями в сослагательном наклонении. Например, «Если бы в 2012 году Барселона выиграла Лигу Чемпионов, то 1 января 2013 г. планета Земля начала бы крутиться в обратную сторону». Поскольку ему соответствует четвёртая строка таблицы истинности, его следует считать истинным, но оно явно ложно, ибо нет никакой причинной связи между исходом спортивных состязаний и траекториями небесных тел. Исследование контрфактуалов является предметом одной из неклассических логик.
Предложенные определения логических союзов позволяют установить значение любого высказывания, построенного по правилам синтаксиса.
Пример 2.1. Рассмотрим высказывание «Если душа телесна, то она не является простой и в то же время бессмертной». Каково будет его истинностное значение, если все составляющие его простые высказывания «душа телесна», «душа проста» и «душа смертна» истинны?
Обозначим высказывание «душа телесна» буквой r, «душа проста» буквой p, а «душа смертна» буквой q. Тогда процесс построения анализируемого сложного высказывания можно представить так, как это изображено на рис. 2.7:
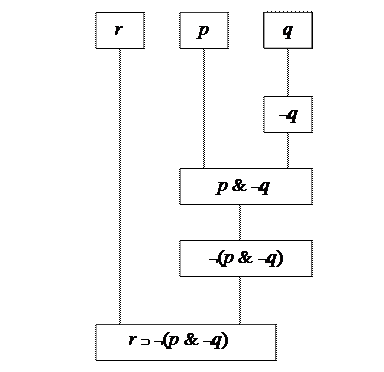
Рис. 2.7
Теперь вычислим его значение, идя по этой схеме сверху вниз. На самом верхнем уровне находятся «кирпичи», из которых строится здание нашего высказывания, т.е. простые высказывания, из которых оно составлено. Спускаясь на один уровень вниз, мы каждый раз выполняем операцию, указанную блоке соответствующего уровня. На первом шаге вычисляется Ø q. Поскольку q истинно, то Ø q ложно. Спускаемся на следующий уровень, где обнаруживаем p &Ø q. Это конъюнкция, первый член которой истинен (по условию), а второй как мы только что установили, ложен. Стало быть, значение этой конъюнкции определяется по второй строке табличного определения конъюнкции. В этом случае наша конъюнкция имеет значение «ложь». Спускаемся ещё на один уровень, здесь только что полученная конъюнкция подвергается отрицанию. Отрицание лжи даёт истину, значит Ø(p &Ø q) является истинным. Наконец, на последнем уровне мы приходим к интересующему нас высказыванию r ÉØ(p &Ø q). Оно представляет собой импликацию с антецедентом r и консеквентомØ(p &Ø q). И антецедент, и консеквент являются истинными. Импликация в этом случае принимает значение «истина». Таким образом, высказывание «Если душа телесна, то она не является простой и в то же время бессмертной» является истинным, когда составляющие его простые высказывания истинны. Описанный процесс вычисления можно представить в виде следующей построчной последовательности, если в высказывании r ÉØ(p & Ø q) подставить вместо переменных их значения:
И ÉØ(И &Ø И)
И ÉØ(И &Л)
И ÉØ(Л)
И É И
И
Кроме того, этот же процесс вычисления можно представить в идее таблицы:
| p | q | r | Ø q | p &Ø q | Ø(p &Ø q) | r ÉØ(p &Ø q) |
| и | и | и | л | л | и | и |
Рис. 2.8.
Первые три столбца таблицы на рис. 2.8 являются входными. Поскольку значения простых высказываний известны, перебор значений требует заполнить всего одну строку, указав в каждом входном столбце заданное значение соответствующей переменной. Столбцы с 4 по 6 содержат результаты промежуточных вычислений. Столбец 7 является выходным, в нём содержится значение анализируемого высказывания.
Аналогичным образом можно установить значение исследуемого высказывания для любого другого набора значений входящих в него простых высказываний.
Обобщение последнего метода позволяет осуществить полный табличный анализ высказывания. Для этого во входных столбцах мы должны отразить все возможные интерпретации имеющегося набора переменных. Мы уже видели, что в случае одной переменной для этого требуется две строки, в случае двух переменных четыре строки. Собственно, количество интерпретаций, соответственно, количество строк в таблице истинности, вычисляется по формуле 2 n, где n – количество переменных. Поэтому для трёх переменных понадобится восемь строк, для четырёх шестнадцать и т.д.
Следующий вопрос в том, как заполнять эти строки, чтобы обеспечить полный перебор всех возможных интерпретаций и избежать повторов. Подсказку можно увидеть, если внимательно посмотреть на то, как заполнялись входные столбцы в табличных определениях логических союзов. В определениях бинарных связок один входной столбец (а именно, для В) дважды повторял единственный входной столбец определения унарной связки. При этом в другом столбце (для А) первый повтор сопровождался значениями «И », а второй значениями «Л ». При добавлении третьей переменой действуем аналогично: дважды повторяем переборы для двух переменных, при этом один перебор сопровождаем значением «И » у третьей переменной, а второй – значением «Л » третьей переменной. Таким образом, при заполнении входных столбцов В одном столбце (здесь это будет крайний справа входной столбец) значения «истина» и «ложь» чередуются по одному. Во втором столбце (здесь – второй справа) по два, в следующем по четыре и т.д. Таким образом, стандартное заполнение входных столбцов для трёх переменных будет выглядеть так (рис.2.9):
| p | q | r |
| и | и | и |
| и | и | л |
| и | л | и |
| и | л | л |
| л | и | и |
| л | и | л |
| л | л | и |
| л | л | л |
Рис. 2.9.
После этого по очереди заполняем промежуточные столбцы. В нашем примере это те же столбцы, что на рис. 2.8, но теперь требуется заполнить каждый столбец для всех восьми интерпретаций. Так, 4-й столбец должен содержать значения Ø q для каждой из восьми интерпретаций. Чтобы заполнить его, в каждой строке смотрим на значение q (2-й столбец) и в той же строке 4-го столбца записываем его отрицание (рис.2.10):
| p | q | r | Ø q | p &Ø q | Ø(p &Ø q) | r ÉØ(p &Ø q) |
| и | и | и | л | |||
| и | и | л | л | |||
| и | л | и | и | |||
| и | л | л | и | |||
| л | и | и | л | |||
| л | и | л | л | |||
| л | л | и | и | |||
| л | л | л | и |
Рис.2.10
Чтобы заполнить 5-й столбец, который содержит значения p &Ø q, в каждой строке обращаем внимание на содержимое 1-го столбца, который содержит значения р, и 4-го, где перечислены значения Ø q. Так, во второй строке р имеет значение «истина», Ø q имеет значение «ложь». Конъюнкция истины и лжи даёт ложь, поэтому во второй строке 5-го столбца пишем «л», и т.д. Аналогичным образом заполняются остальные столбцы, вплоть до выходного. Полностью заполненная истинностная таблица нашего высказывания такова (рис. 2.11):
| p | q | r | Ø q | p &Ø q | Ø(p &Ø q) | r ÉØ(p &Ø q) |
| и | и | и | л | л | и | и |
| и | и | л | л | л | и | и |
| и | л | и | и | и | л | л |
| и | л | л | и | и | л | и |
| л | и | и | л | л | и | и |
| л | и | л | л | л | и | и |
| л | л | и | и | л | и | и |
| л | л | л | и | л | и | и |
Рис. 2.11
Полный анализ нашего высказывания показывает, в частности, что оно ложно только на одной интерпретации, представленной третьей строкой: r (душа телесна) и p (душа проста) истинны, а q (душа смертна) ложно. Во всех остальных случаях оно будет истинным.
Мы ввели в наш язык так называемые основные логические связки. Они наиболее употребимы в естественном рассуждении. Например, можно было бы задать такую связку, как несовместимость, обозначив «А несовместимо с В » через А ∣ В, и определив её с помощью следующей таблицы:
| А | В | А ∣ В |
| и | и | л |
| и | л | и |
| л | и | и |
| л | л | и |
Рис. 2.12
Однако можно заметить, что выходной столбец этой связки можно получить, подвергнув отрицанию конъюнкцию А & B. Поэтому её можно ввести не в качестве основной, но с помощью определения, как сокращение для выражения Ø(А&B). Логический союз «ни А, ни В », символически А ↓ В, определяемый таблицей
| А | В | А ↓ В |
| и | и | л |
| и | л | л |
| л | и | л |
| л | л | и |
Рис. 2.13
имеет выходной столбец, который можно получить, отрицая дизъюнкцию А Ú В. Поэтому, аналогично предыдущему примеру, эту связку тоже можно ввести с помощью определения, как сокращение для Ø(А Ú B).
Ещё один достойный внимания логический союз – «только если…, то …». «только если» – это не то же самое, что «если» и не то же самое, что «если и только если». Попытаемся установить его условия истинности, рассмотрев пример. «Иван смотрит только комедийные фильмы». Это предложение можно переформулировать, чтобы логическая структура выражаемого им высказывания стала более прозрачной: «Только если фильм комедийный, то Иван его смотрит». Обозначим через р простое высказывание «этот фильм – комедия», а через q «Иван смотрит этот фильм». Теперь заполним выходной столбец, если ситуация описываемая в строке, возможна, ставим в в этой строке выходного столбца значение «и»; если такая ситуация исключена, ставим в этой строке ложь. Так, в первой строке описана ситуация, в которой истинно, что этот фильм – комедия, и истинно, что Иван смотрит этот фильм. Разумеется, эта ситуация вполне возможна, поэтому в первой строке выходного столбца стоит «И». Вторая строка содержит такую интерпретацию, что этот фильм – комедия, но Иван его не смотрит. Она не исключена! Согласно условию, Иван смотрит только комедии, но при этом не оговорено, что Иван смотрит все комедии без исключения. Зато ситуация, описанная, описанная третьей строкой: этот фильм не комедия и Иван его смотрит, несомненно, исключена. Поэтому в третьей строке должно быть вписано значение «Л». Наконец, достаточно очевидно, что в четвёртой строке выходного столбца имеется значение «И».
| р | q | |
| и | и | и |
| и | л | и |
| л | и | л |
| л | л | и |
Итак, выходной столбец в полученной таблице истинности действительно не соответствует ни импликации, ни эквиваленции. Высказывание с таким выходным столбцом ложно в том и только в том случае, когда q истинно, а р ложно. Но ведь последнее есть не что иное, как определение импликации для высказывания с антецедентом q и консеквентом р. Значит, высказывания «Только если этот фильм комедия, то Иван его смотрит» и «Если Иван смотрит фильм, то этот фильм – комедия» имеют одинаковые условия истинности. Поэтому «только если А, то В » можно выразить как «А, если В ». Союз «только если» можно назвать обратной импликацией (его также называют «репликация »), и ввести для его обозначения отдельный символ: А Ì В. Но, с учётом сделанных разъяснений, это можно выразить с помощью обычной импликации, поменяв местами соединяемые этим союзом высказывания: В É А.
Вообще говоря, всего с помощью механического комбинирования, т.е. перебирая все возможные комбинации значений «И » и «Л » в выходном столбце, можно задать 16 бинарных связок. При этом одни из них будут не особенно полезными (например, когда выходной столбец содержит только значения «И » или только значения «Л », или когда выходной столбец совпадает с одним из входных и т.п.), а другие легко сводимыми к тем связкам, которые только что нами определены.
[1] Следует отметить, что отсутствует общепринятая трактовка термина «высказывание». Многие авторы понимают под ним «предложение, взятое вместе со своим смыслом».
[2] Здесь можно сделать замечание, что слова «правильно построенное» являются избыточными, поскольку неправильно построенного высказывания не может быть просто потому, что всё, что построено не по правилам, не будет являться никаким высказыванием, а будет лишь бессмысленным набором символов.