Не смотря на то, что меню Simulation ( моделирование) содержит всего несколько команд (рис. 19), именно они играют основную роль при проведении исследований модели. Посредством этих команд разработчик получает возможность не только динамически управлять сеансом моделирования, но и изменять многие важнейшие параметры модели, такие, например, как способ изменения модельного времени, алгоритм расчета и формат представления результатов моделирования.
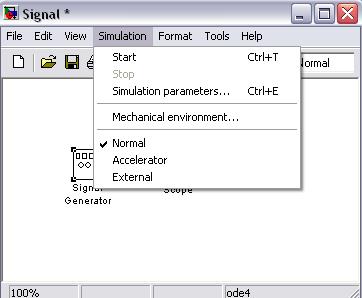
Рис. 19. Меню Simulation
Рассмотрим подробнее средства управления моделью и параметрами сеанса моделирования, которые предоставляет исследователю окно Simulation Parameters (параметры моделирования), рис. 20. Элементы управления на вкладке Solver собраны в три группы.
Simulation time (интервал моделирования) – выбор интервала моделирования посредством указания начального (Start time) и конечного (Stop time) значений модельного времени.
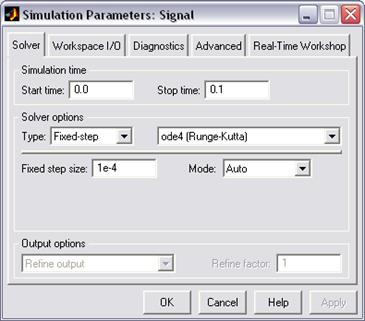
Рис. 20. Окно установки параметров моделирования
Solver options (параметры расчета) – выбор метода реализации (расчета) модели.
Output options (параметры вывода) – параметры вывода выходных параметров моделируемой системы (при моделировании с переменным шагом).
Под выбором метода реализации модели имеется в виду следующее. Имея структуру исследуемой системы в виде блок–диаграммы, разработчик может выбрать метод отображения хода моделирования. С помощью двух раскладывающихся списков Type (Тип) система может быть реализована в следующих формах:
· с дискретными состояниями и дискретным временем перехода из одного состояния в другое;
· с дискретными состояниями и непрерывным временем перехода;
· с непрерывными состояниями и дискретным временем переходов;
· с непрерывными состояниями и непрерывным временем переходов.
|
|
Первый список (слева) позволяет выбрать способ изменения модельного времени:
· Variable – step (переменный шаг) – моделирование с переменным шагом;
· Fixed – step (фиксированный шаг) – моделирование с фиксированным шагом.
Второй список (справа) позволяет выбрать метод расчета нового состояния системы. Первый вариант (discrete) обеспечивает расчет дискретных состояний системы. Остальные пункты списка обеспечивают выбор метода расчета нового состояния для непрерывных систем. Эти методы различаются для переменного (Variable – step) и для фиксированного (Fixed – step) шага времени, но основаны на единой методике – решение обыкновенных дифференциальных уравнений(ode).
Ниже двух раскрывающихся списков Type находится поле, название которого изменяется в зависимости от выбранного способа изменения модельного времени (рекомендуется оставить параметры по умолчанию).
Параметры других вкладок также можно использовать по умолчанию.
3. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
При выполнении лабораторной работы используется программа MATLAB версии 6.0 и выше.
4. ПРОГРАММА ЛАБОРАТОРНОЙ РАБОТЫ
4.1 Изучить особенности синтеза БИХ-фильтра методом билинейного преобразования в пакете программ MATLAB.
4.2 Выполнить синтез БИХ-фильтра, проанализировать расположение полюсов и нулей фильтра на комплексной Z-плоскости, рассчитать коэффициенты передаточной функции ЦФ, проверить соответствие АЧХ заданным требованиям.
4.3 Найти переходную характеристику фильтра.
4.4 Найти отклики фильтра на гармонические сигналы в полосе пропускания и полосе задерживания, оценить избирательные свойства фильтра.
|
|
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
5.1. Что такое импульсная характеристика и передаточная функция ЦФ?
5.2. Что такое порядок ЦФ и как сказывается его значение при реализации фильтра?
5.3. Что такое нули и полюса передаточной функции ЦФ?
5.4. Как определить устойчивость ЦФ по значениям его нулей и полюсов?
5.5. Что такое билинейная преобразующая функция? Как преобразуются частоты аналогового и цифрового фильтров при билинейном преобразовании?
5.6. Как определяются требования к аналоговому фильтру-прототипу в методе билинейного преобразования?
5.7. Каковы особенности аппроксимирующих функций, используемых при синтезе ЦФ? Как зависит порядок синтезируемого ЦФ от вида аппроксимирующей функции?
5.8. Какие параметры фильтра позволяет визуально просмотреть окно Filter Visualization Tool блока параметров Digital Filter Design?
5.9. Для чего используется блок Gain при моделировании работы ЦФ?
5.10. Каково назначение блока Zero-Order Hold при моделировании работы ЦФ?
5.11. Каким образом задается период дискретизации блока Zero-Order Hold и чему он должен быть равен?
5.12. Какие параметры необходимо установить, чтобы на выходе блока Step получить непрерывное/дискретное ступенчатое воздействие?
6. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОГО ЗАДАНИЯ
6.1 Создать модель фильтра (п. 2.5.1) в программе Simulink.
Подготовить и ввести в программу исходные данные (п. 2.5.1) в соответствии с заданным вариантом (по номеру компьютера), необходимые для синтеза цифрового ФНЧ: аппроксимация – по Чебышеву 1 (п. 2.7.2); частота среза Fс; коэффициент усиления K0; порядок фильтра-прототипа N=2, пульсации в полосе пропускания – 1дБ.
|
|
| Вариант | ||||||
| Fс | 100 Гц | 200 Гц | 300 Гц | 400 Гц | 500 Гц | 600 Гц |
| K0 |
Частоту дискретизации установить равной 4 кГц.
6.2 Произвести синтез фильтра. Просмотреть и проанализировать следующие параметры фильтра: расположение полюсов и нулей фильтра на Z-плоскости, коэффициенты передаточной функции, АЧХ.
6.3 Подать на вход ЦФ единичное ступенчатое воздействие (п. 2.5.5) и вычислить переходную характеристику системы.
6.4 Подать на вход ЦФ импульс Кронекера и вычислить импульсную характеристику системы.
6.5 Подать на вход ЦФ гармонический сигнал (п. 2.5.3) с частотой Fx равной частоте среза фильтра Fc и единичной амплитудой. Построить графики входного и выходного сигнала. Оценить избирательные свойства фильтра.
6.6 Повторить п.6.5 для гармонического сигнала с частотой Fx=2×Fc.
6.7 Повторить пункты 6.1 – 6.6 для цифрового полосового фильтра (ПФ) с аппроксимацией Баттерворта 2 порядка: центральная частота полосы пропускания Fс; коэффициент усиления K0, полоса пропускания DF=0.1×Fc.
| Вариант | ||||||
| Fс | 100 Гц | 200 Гц | 300 Гц | 400 Гц | 500 Гц | 600 Гц |
| K0 |
Частоту дискретизации установить равной 4 кГц.
6.8 Повторить пункты 6.1 – 6.6 для цифрового режекторного фильтра (РФ) с аппроксимацией Баттерворта 2 порядка: центральная частота полосы заграждения Fс; коэффициент усиления K0, полоса заграждения DF=0.1×Fc.
| Вариант | ||||||
| Fс | 100 Гц | 200 Гц | 300 Гц | 400 Гц | 500 Гц | 600 Гц |
| K0 |
Частоту дискретизации установить равной 4 кГц.
7. СПИСОК ЛИТЕРАТУРЫ
1. Глинченко А.С. Цифровая обработка сигналов: учебное пособие. В 2 ч. Ч.1. – Красноярск: Изд-во КГТУ, 2001. – 199 с.
2. Гультяев А. К. Визуальное моделирование в среде MatLab. Учеб. курс. – СПб.: Питер, 2000. – 480 с.
3. Гультяев А. К. MatLab. Иммитационное моделирование в среде Windows: учебное пособие. – СПб.: КОРОНА Принт, 1999. – 288 с.
4. Гольденберг Л.М. и др. Цифровая обработка сигналов. – 2-е изд., перераб. и доп. – М.: Радио и связь, 1990. – 256 с.
5. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. / Пер. с англ. под ред. Ю.Н. Александрова. – М.: Мир, 1978. – 848 с.
6. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 604 с.