ТМК – 270843 – ТОЭ – ПР – 01
Дисциплина: Теоретические основы электротехники
МЕТОДИКА
Выполнения практической работы № 1
«Расчет цепей постоянного тока методом контурных токов»
| Преподаватели | Председатель комиссии энергетических дисциплин | Заместитель директора по научно-методической работе | Заместитель директора по учебной работе |
| Г. Погорелов Н.Головченко Е.Налимова М.Остапенко | Г. Погорелов | Л. Архипова | В. Макаренко |
Практическая работа №1
Расчет цепей постоянного тока методом контурных токов
Цель работы
Получение практических навыковрасчета цепей постоянного тока методом контурных токов с применением системы компьютерной математики MathCAD и моделирования схем с заданными параметрами с помощью пакета виртуального моделирования Proteus 7 Professional.
Задание
2.1 Рассчитать параметры электрической схемы:
методом определителей;
с применением системы MathCAD;
с помощью пакета виртуального моделирования Proteus 7 Professional.
2.2 Проверить правильность полученных значений токов по первому закону Кирхгофа.
2.3 Составить баланс мощностей:
Исходные данные
Таблица 1 Исходные данные
| № вар. | № схем. | Е1 | Направлен.Е1 | Е2 | Направлен.Е2 | R1 | R2 | R3 | R4 | R5 | R6 |
| - | - | В | - | В | - | Ом | Ом | Ом | Ом | Ом | Ом |
| От А к В | От С к D | ||||||||||
| От B к C | От C к D | ||||||||||
| От A к C | От D к C | ||||||||||
| От A к C | От A к D | ||||||||||
| От D к B | От A к D | ||||||||||
| От C к B | От В к D | ||||||||||
| От A к D | От D к C | ||||||||||
| От A к C | От A к D | ||||||||||
| От A к C | От B к D | ||||||||||
| От A к С | От A к В | ||||||||||
| От B к A | От C к D | ||||||||||
| От C к B | От C к D | ||||||||||
| От C к A | От D к C | ||||||||||
| От C к A | От A к D | ||||||||||
| От D к A | От D к B | ||||||||||
| От B к C | От C к D | ||||||||||
| От D к A | От D к C | ||||||||||
| От C к A | От A к D | ||||||||||
| От C к A | От B к D | ||||||||||
| От B к A | От A к C | ||||||||||
| От A к B | От D к C |
Продолжение Таблицы 1
| № вар. | № схем. | Е1 | Направлен.Е1 | Е2 | Направлен.Е2 | R1 | R2 | R3 | R$ | R5 | R6 |
| От B к C | От D к C | ||||||||||
| От A к C | От C к D | ||||||||||
| От A к C | От D к A | ||||||||||
| От D к A | От B к D | ||||||||||
| От C к B | От D к C | ||||||||||
| От D к A | От C к D | ||||||||||
| От A к C | От D к A | ||||||||||
| От A к C | От D к B | ||||||||||
| От A к B | От C к A | ||||||||||
| От B к A | От D к C | ||||||||||
| От C к B | От D к C | ||||||||||
| От C к A | От D к C | ||||||||||
| От C к A | От D к A | ||||||||||
| От A к D | От B к D |
Схема 1 Схема 2
Схема 3 Схема4
Схема 5 Схема 6
Схема 7 Схема 8
Схема 9 Схема 10
Выполнение работы
4.1 Вычерчиваем расчетную схему.
4.2 В соответствии с исходными данными проставляем стрелками направление ЭДС источников электроэнергии. В каждой ветви схемы проставляем направление тока и его обозначение.
Примечание: Обозначение тока необходимо производить в соответствии с индексом соответствующего элемента ветви; например, в ветви с сопротивлением R1 обозначение тока должно быть I1 и т.д.
4.3 Выделяем в схеме независимые контуры и проставляем для каждого контура обозначение контурного тока и его направление.
Примечание: Каждый контурный ток рекомендуется обозначать индексом с двумя одинаковыми цифрами; например, I11, I22 и т.д.; направление протекания всех контурных токов рекомендуется принимать одинаковыми, например, по часовой стрелке.
4.4. Для каждого контура составляем уравнение по второму закону Кирхгофа; решаем полученную систему уравнений
4.4.1 Решаем систему уравнений методом определителей;
4.4.2 Определяем действительные значения токов во всех ветвях схемы. Примечание: Действительное значение тока в любой из ветвей схемы может получиться со знаком минус. Это говорит о том, действительное направление тока в ветви противоположно проставленному на схеме.
4.4.3 Производим проверку полученных значений токов по первому закону Кирхгофа для каждого узла схемы.
4.4.4 Определяем параметры схемы с применением системы MathCAD;
4.5 Составляем баланс мощностей схемы.
Примечание: Значение мощности источника ЭДС может получиться со знаком минус. Это говорит о том, что данный источник работает в режиме потребителя электроэнергии.
4.6 Моделируем схему с заданными параметрами с помощью пакета Proteus.
Пример выполнения работы
Таблица 2 Исходные данные
| № вар. | № схем. | Е1 | Направлен.Е1 | Е2 | Направлен.Е2 | R1 | R2 | R3 | R4 | R5 | R6 |
| - | - | В | - | В | - | Ом | Ом | Ом | Ом | Ом | Ом |
| От A к C | От D к A |
5.1 Вычерчиваем расчетную схему.
5.2 В соответствии с исходными данными проставляем стрелками направление ЭДС источников электроэнергии. В каждой ветви схемы произвольно проставляем направление тока и его обозначение.
5.3 Выделяем в схеме независимые контуры и проставляем для каждого контура обозначение контурного тока и его направление.
5.4 Для каждого контура составляем уравнение по второму закону Кирхгофа.
Для первого контура I11(R1+R2+R3)-I22R2-I33R3=E1 (1)
Для второго контура I22(R2+R4+R5)-I11R2-I33R5=E2 (2)
Для третьего контура I33(R3+R5+R6)-I11R3-I22R5=0 (3)
5.4.1Решение системы уравнений при помощи определителей
5.4.1.1 Исходная система уравнений:
I11(R1+R2+R3)-I22R2-I33R3=E1 (1)
I22(R2+R4+R5)-I11R2-I33R5=E2 (2)
I33(R3+R5+R6)-I11R3-I22R5=0 (3)
5.4.1.2 Подставляем значения ЭДС и сопротивлений и записываем уравнения в порядке возрастания индекса токов
I11(6+8+4)-I22 8-4I33=120 (1)
I22(8+10+2)-I118-I332=100 (2)
I33(4+2+12)-I114 -I222=0 (3)
18·I11-8·I22 -4·I33=120
-8·I11+20·I22 -2·I33=100 (4)
-4·I11 -2·I22 +18·I33=0
5.4.1.3 Составляем определитель системы и определитель свободных членов,
вычисляем определитель системы
| -8 | -4 | |
| -8 | -2 | |
| -4 | -2 |
∆ =
∆b =
5.4.1.4 Составляем и вычисляем определитель ∆11
| -8 | -4 | |
| -2 | ||
| -2 |
∆11 =
5.4.1.5 Составляем и вычисляем определитель ∆22
| -4 | ||
| -8 | -2 | |
| -4 |
∆22 =
5.4.1.6 Составляем и вычисляем определитель ∆33
| -8 | ||
| -8 | ||
| -4 | -2 |
∆33 =
5.4.1.7 Определяем значения контурных токов
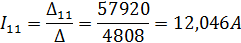
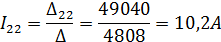
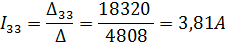
5.4.1.8 Производим проверку правильности расчета контурных токов, подставляя их значения в систему уравнений (4) п. 5.4.1.2
18·I11-8·I22 -4·I33=120; 18·(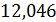
) - 8(
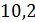) - 4·(
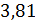) = 120;
216,828 – 81,6 - 15,24 = 120; 119,988≈120
-8·I11+20·I22 -2·I33=100; -8(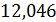) + 20(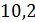) – 2(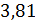) = 100;
-96,368 +204-7,62 = 100; 100,012≈100
-4·I11 -2·I22 +18·I33=0; -4(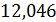) - 2(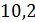) + 18(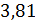) = 0;
–48,184-20,4+68,58 = 0; - 0,004 ≈ 0.
5.4.1.9 Находим истинное значение тока в каждой ветви схемы.
I1= I11= 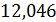А; I2= I22 - I11 = 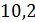- 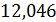= - 1,826А;
I3 = I33 - I11 = 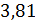- 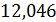= - 8,236А; I4 = I22 = 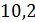А;
I5 = I33 - I22 = 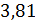- 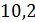= - 6,39А; I6 = I33 = 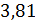А
5.5 Для каждого узла схемы составляем уравнение по первому закону Кирхгофа:
Для узла А: I4 = I1 + I2; 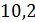= 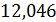+(- 1,826); 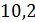≈ 10,119
Для узла В: I2 + I5 = I3; - 1,826 + (- 6,39) = - 8,236; - 8,216 ≈ - 8,236
Для узла C: I1 + I3 = I6; 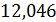+ (- 8,236) = 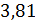; 3,81 =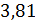
Для узла D: I6 = I4 + I5; 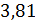= 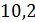+(- 6,39); =
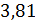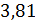
5.6 Производим расчет баланса мощностей.
5.6.1 Определяем мощность, отдаваемую источниками электроэнергии
PЕ1 = I1 Е1 = 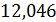·120 = 1445,52 Вт
PЕ2 = I4 Е2 = 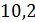· 100 = 1020 Вт
5.6.2 Определяем напряжение на каждом сопротивлении
U1 = I1·R1 = 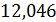·6 = 72,276 В
U2 = I2·R2 = - 1,826·8 = -14,608 В
U3 = I3·R3 = - 8,236·4 = -32,944 В
U4 = I4·R4 = 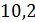·10 = 102 В
U5 = I5·R5 = - 6,39·2 = -12,78 В
U6 = I6·R6 = 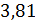·12 = 45,72 В
5.6.3 Определяем мощность, потребляемую каждым сопротивлением схемы
P R 1 = I1 U1 = 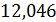· 72,276 = 870,367 Вт
P R 2 = I2 U2 = - 1,826 ·(- 14,608) = 26,674 Вт
P R 3 = I3 U3 = - 8,236 · (-32,944) = 271,327 Вт
P R 4 = I4 U4 = 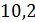· 102 = 1040,4 Вт
P R 5 = I5 U5 = - 6, 39 · (-12, 78) = 81,664 Вт
P R 6 = I6 U6 = 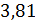· 45,72 = 174,193 Вт
5.6.3 Составляем баланс мощностей
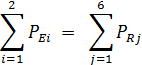
1495,2 +1020=870,367+26,674+271,327+1040,4+81,664+174,193
2465,52 ≈ 2464,625
Заносим значения исходных данных и результатов расчета в таблицу 3
Таблица 3 Результаты расчета
| Пара-метр | Единица изме-рения | Элементы схемы | |||||||
| Е1 | Е2 | R1 | R2 | R3 | R4 | R5 | R6 | ||
| 120 В | 100 В | 6 Ом | 8 Ом | 4 Ом | 10 Ом | 2 Ом | 12 Ом | ||
| I | А |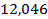 
| 
|
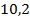
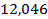
| - 1,826 | - 8,236 |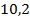
| - 6,39 |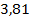 
|
| U | В | - | - | 72,276 | -14,608 | -32,944 | -12,78 | 45,72 | |
| P | Вт | 1445,52 | 870,367 | 26,674 | 271,327 | 1040,4 | 81,664 | 174,193 | |
| Баланс | Вт | ∑ 2465,52 | ∑ 2464,625 |
5.7 Выполнение расчета с применением компьютера
5.7.1 Ввод исходных данных
Задаем матрицу A коэффициентов системы линейных уравнений.
Аналогично определяем вектор свободных членов системы уравнений B.
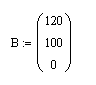
Вычисляем определитель матрицы А
Определитель не равен нулю, а это значит, что система имеет единственное решение. Найдем его несколькими способами.
5.7.2Решение системы линейных уравнений матричным способом:
Вводим формулу, определяющую решение системы в матричном виде: умножение обратной матрицы коэффициентов на вектор свободных членов.
5.7.3 Решаем систему линейных уравнений с помощью встроенной функции lsolve:
Ввожим строку l so l ve(A,B), в которой функция lsolve находит решение системы линейных уравнений, заданной матрицами А и В.
5.7.4 Решаем систему линейных уравнений с помощью вычислительного блока Given/Find:
Для того чтобы решить систему линейных уравнений с помощью вычислительного блока Given - Find, необходимо:
Ø задаем начальные приближения для всех переменных;
Ø вводим служебное слово Given;
Ø записываем систему уравнений, используя логический знакравенства;
Ø записываем функцию Find, перечислив неизвестные переменные в качестве параметров функции.
В результате расчетов вводится вектор решения системы.
5.7.5 Результаты выполнения работы в системе Mathcad:
5.8 Проверим расчеты параметров схемы с помощью системы виртуального моделирования Proteus 7 Professional.
