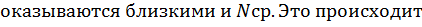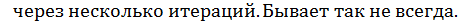Процесс размножения-гибели
Марковский процесс, с помощью которого была построена математическая модель в примере 2.8, является представителем важного класса марковских процессов – процессов размножения-гибели (ПРГ). Для ПРГ решение СЛАУ относительно стационарных вероятностей состояния записывается в явном виде.
ПРГ – это марковский процесс, граф переходов которого имеет такой вид, как на рис. 2.4. Каждое состояние в нем связано с двумя соседними, каждое из двух крайних связано с одним соседним.

Рис. 2.4. Граф переходов ПРГ
Для получения выходных параметров систем обслуживания часто бывает достаточно вычислить значения стационарных вероятностей 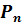 .
.

Вероятность 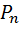 равна средней доле времени, проведенного системой в состоянии
равна средней доле времени, проведенного системой в состоянии 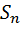 .
.
Эта система может быть получена непосредственно из графа по правилу «что входит, то и выходит» (принцип сохранения потока). Решение системы с учетом уравнения нормировки
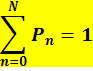
легко получить в явном виде последовательным выражением вероятностей 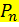 для
для 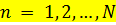 через
через 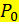 и подстановкой их в уравнение нормировки.
и подстановкой их в уравнение нормировки.
Попробуем. Вернемся к графу и уравнениям
 . Из второго . Из второго
 сокращая сокращая 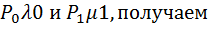 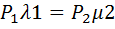 ; отсюда ; отсюда 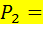 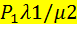 Или
Или 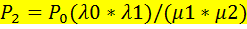 Продолжая так же, получаем
Продолжая так же, получаем
 или или 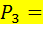 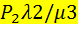
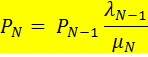

| (2.41) |
Подставляем все 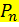 , выраженные через
, выраженные через 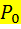 в уравнение нормировки
в уравнение нормировки
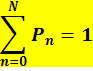
В результате получим, что для ПРГ решение СЛАУ относительно стационарных вероятностей состояния имеет вид:
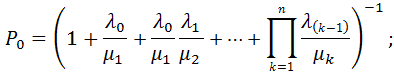 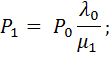 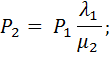 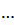 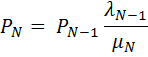
| (2.49) |
Дальше считаем Nср, M[Тр] и другие выходные параметры.
Почти одинаково считаются разомкнутые модели М/М/1, М/М/2, М/М/3,…(с любым числом процессоров и одним внешним пуассоновским потоком) и замкнутые модели
М/М/1/N (это как раз пример 2.8), М/М/2/N, М/М/3/N,…(с любым числом процессоров и N терминалами).
У них очень похожие графы переходов.
Например система М/М/К/N. В ней N (допустим, 100), терминалов и К ОА (К параллельно работающих процессоров, допустим, К = 7)
Назовем условно в графе строку лямбд строкой числителей, а строку мю строкой знаменателей. А между ними строка состояний (количества запросов в системе – в очереди и в процессорах – от нуля до 100).
И тогда строка числителей (коэффициентов при λ) – от 100 до 1, а строка знаменателей – от 1 до 7, а дальше сплошные семерки, потому что она (коэффициенты при μ) определяется формулой C(i)=min(i,К). То есть, сколько процессоров занято обслуживанием, когда в системе i заявок.
В Excel все эти три строки графа удобно расположить по вертикали (их от 0 до 100, а захотел –тут же можно расширить и до 250 или 500. (формулы однотипные –для двух –трех n написал – и протянул вниз до 500. Только формулы для суммы надо написать вверху (типа «от 0 до 2000») на всякий случай, чтобы не лазать вниз менять их при изменении N, и сразу было видно, что сумма вероятностей равна 1
Потом считается столбец коэффициентов (начиная с 1, а каждый следующий равен предыдущему, умноженному на предыдущий числитель, деленному на текущий знаменатель и умноженному на ρ=λ/μ. Тянем вниз до N или дальше (предусмотрев, чтобы дальше N были нули (например, через формулу в строке числителей)
Р0 - это сумма всех коэфф-тов. Сами сообразите, какая формула
в строке Р1 и дальше (опять через числители и знаменатели). Сообразите про формулы столбца для получения среднего значения (Nср) и эффективной производительности.
И потом среднее время реакции исходя из принципа: В замкнутых системах среднее время в каждой части системы пропорционально среднему числу требований в ней.
Проверяйте реализацию: сумма вероятностей равна 1, меняйте исх. данные для проверки правдоподобия поведения модели и т.д.
Марковская модель, но не ПРГ.
Агрегирование с использованием параметра связи
В настоящей главе рассмотрим примеры структурно более сложных марковских моделей, а на их основе – методы повышения вычислительной эффективности моделей, в результате чего становится возможным проведение многовариантных расчетов [18].
Пример 3.1
Рассмотрим модель, которая была актуальна в начале 70-х годов прошлого столетия, накануне появления персональных компьютеров. Сейчас она полезна с точки зрения методологии анализа структурно более сложных марковских моделей. Тогда она использовалась как инструмент анализа ядра комплекса технических средств (КТС) специализированной автоматизированной системы обработки данных, позволяющий определить характеристики КТС в зависимости от структурных и технических параметров входящих в КТС элементов. Упрощенная структура модели показана на рис.3.1.
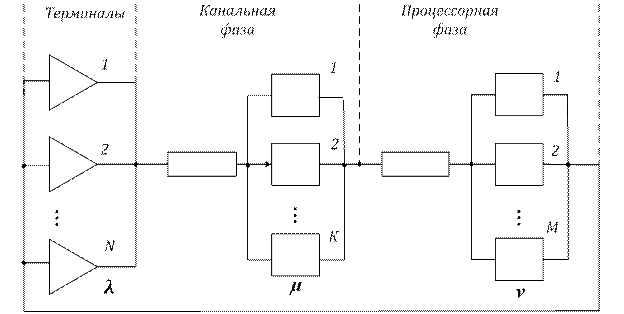
Рис. 3.1. Структура модели
В модели отдельно показана подсистема обработки (процессорная фаза), включающая в себя несколько параллельных процессоров, и подсистема обмена (канальная фаза), включающая в себя селекторные каналы и накопители на магнитных дисках (НМД). Пусть каждый запрос пользователя требует решения задачи в процессоре и обмена информацией между ОП и НМД, осуществляемый посредством селекторного канала. В зависимости от конкретного варианта подключения НМД к селекторным каналам и распределения задач пользователей по НМД получаются различные формализованные схемы подсистемы обмена. Рассмотрим один из вариантов, состоящий в том, что имеется общая очередь заявок к совокупности селекторных каналов, из которой заявки выбираются в порядке их поступления.
Пусть система содержит 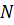 терминалов,
терминалов, 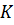 селекторных каналов и
селекторных каналов и 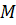 процессоров.
процессоров.
Если принять допущение, что время решения задачи в процессоре, время обмена информацией между оперативной и внешней памятью и время обдумывания задачи пользователем (время между соседними запросами одного пользователя) представляют собой независимые СВ, имеющие экспоненциальные распределения, то изменение состояния системы во времени может быть описано марковским случайным процессом. В такой модели среднее время реакции M[ 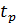 ] является функцией параметров
] является функцией параметров 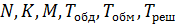 .
.
При этом первые моменты ФР указанных случайных величин равны соответственно:
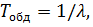 ,
, 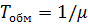 ,
, 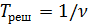 .
.
В качестве состояния системы в момент 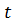 можно взять вектор
можно взять вектор 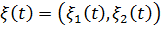 , где
, где 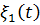 - число пользователей в момент
- число пользователей в момент 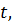 осуществляющих обдумывание своей задачи (число заявок на фазе терминалов), а
осуществляющих обдумывание своей задачи (число заявок на фазе терминалов), а 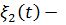 число задач в момент
число задач в момент 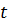 , осуществляющих обмен или ожидающих обмена между оперативной и внешней памятью (число заявок на фазе каналов обмена).
, осуществляющих обмен или ожидающих обмена между оперативной и внешней памятью (число заявок на фазе каналов обмена).
Тогда число заявок на фазе процессоров равно 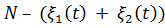 .
.
Граф переходов модели для частного случая 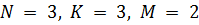 и структура фрагмента графа переходов (показаны только исходящие дуги) для общего случая изображены на рис. 3.2.
и структура фрагмента графа переходов (показаны только исходящие дуги) для общего случая изображены на рис. 3.2.
а)
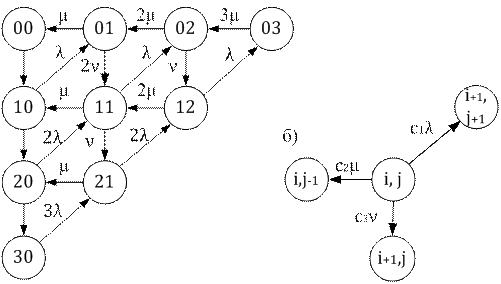
Рис. 3.2. Граф переходов (a) и структура фрагмента графа (b)
(записаны только исходящие интенсивности) Здесь обозначено:
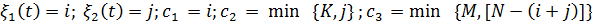 . Исходя из структуры графа переходов, в соответствии с общим правилом можно записать систему линейных алгебраических уравнений (СЛАУ) относительно компонент стационарного распределения вероятностей состояния системы. Написать решение этой системы в явном виде не удается, поэтому в процедуре расчета выходных параметров, осуществляемого с помощью ЭВМ, был предусмотрен блок формирования матрицы коэффициентов системы уравнений и обращение к стандартной программе решения СЛАУ методом Гаусса. Имея значения
. Исходя из структуры графа переходов, в соответствии с общим правилом можно записать систему линейных алгебраических уравнений (СЛАУ) относительно компонент стационарного распределения вероятностей состояния системы. Написать решение этой системы в явном виде не удается, поэтому в процедуре расчета выходных параметров, осуществляемого с помощью ЭВМ, был предусмотрен блок формирования матрицы коэффициентов системы уравнений и обращение к стандартной программе решения СЛАУ методом Гаусса. Имея значения 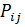 компонент стационарного распределения, можно вычислить среднее количество заявок на терминальной фазе
компонент стационарного распределения, можно вычислить среднее количество заявок на терминальной фазе 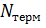 , а также среднее время реакции системы
, а также среднее время реакции системы 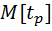
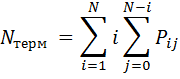

| (3.1) (3.2) |
СЛАУ относительно стационарных вероятностей состояния, а также соотношения (3.1) и (3.2) могут рассматриваться как базисная модель оценки характеристик производительности КТС.
Входящие в эту модель параметры 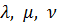 являются функциями технических характеристик процессоров, селекторных каналов и накопителей на магнитных дисках, а также характеристик решаемых в системе задач пользователей. Эта связь устанавливается с помощью интерфейсных моделей.
являются функциями технических характеристик процессоров, селекторных каналов и накопителей на магнитных дисках, а также характеристик решаемых в системе задач пользователей. Эта связь устанавливается с помощью интерфейсных моделей.
1 Чтобы убедиться, что вы поняли, как строится граф, попробуйте его построить, взяв за состояние не (i, j)= (число заявок на фазе терминалов, число заявок на фазе каналов), а
(i, j)= (число заявок на фазе каналов, число заявок на фазе процессоров).
Нарисуйте интенсивности и запишите их для общего случая
2 Попробуйте записать уравнения для какого-то конкретного состояния (i,j).
Представите мне – Вам кружок.
Но считать так плохо, даже если найдем подходящий софт для решения СЛАУ. Допустим, 50 терминалов. Не очень большая система. Треугольный граф 51х51/2 + мелочи ≅ 1350 уравнений с таким же количеством переменных, в сумме равных единице. Анализировать эти переменные (где там узкие места) – отдельная проблема.
Нужны изменения методики инженерного анализа. Аналогичная ситуация и в других инженерных отраслях (см., например, Н.Н. Моисеев, Математические задачи системного анализа, второе изд., гл. 8, Некоторые проблемы автоматизации проектирования, в которой предлагается схема декомпозиции при автоматизированном проектировании сложных систем).
Вообще декомпозиция лежит в основе проектирования любых сложных систем – начиная от больших зданий, мостов, туннелей, паровозов и автомобилей, и кончая самолетами, ракетами, космическими аппаратами и системами управления, энергетическими системами и чем угодно еще.
Рассмотрим один из методов декомпозиции на примере анализа рассмотренной марковской модели. Идея метода состоит в том, чтобы анализ сложной по структуре модели производить по частям, с помощью совокупности частично укрупненных («агрегированных») моделей. В каждой из таких моделей подробно представлена некоторая часть системы, а влияние остальных частей отражается некоторым обобщенным параметром (параметром связи). В итоге получается система уравнений, описывающих изменение состояния каждой из агрегированных моделей. Эти уравнения приходится решать совместно, так как в качестве переменных они содержат и параметры связи.
Рассмотрим вариант реализации метода агрегирования на примере модели примера 3.1, представленной на рис. 3.1, с использованием параметра связи.
Пример 3.2. Для модели, структура которой представлена на рис. 3.1, получить расчетные соотношения для выходных параметров в явном виде (не обращаясь к стандартной программе решения системы линейных алгебраических уравнений). Для этого рассмотрим две агрегированные модели, АМ1 и АМ2.
Модель АМ1. В агрегированной модели АМ1 канальная и процессорная фаза представлены укрупненно – одним агрегированным узлом - ОА с очередью, который описывается обобщенным параметром 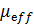 - средней производительностью в обработке запросов, зависящей от среднего числа заявок в этом узле. В качестве состояния системы в момент
- средней производительностью в обработке запросов, зависящей от среднего числа заявок в этом узле. В качестве состояния системы в момент 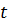 берется
берется 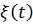 - количество запросов в очереди или на обслуживании. Структура модели АМ1 и граф переходов изображены на рис. 3.3, а и б соответственно.
- количество запросов в очереди или на обслуживании. Структура модели АМ1 и граф переходов изображены на рис. 3.3, а и б соответственно.
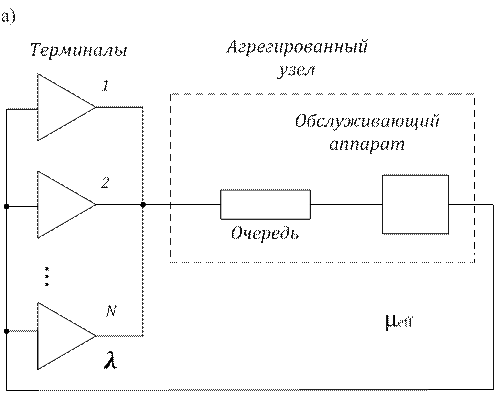
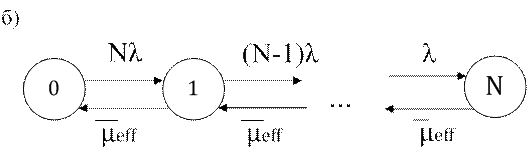
Рис. 3.3. Структура модели АМ1 (a) и граф переходов (б)
Поскольку процесс 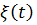 относится к классу ПРГ, решение системы уравнений относительно стационарных вероятностей записывается в явном виде:
относится к классу ПРГ, решение системы уравнений относительно стационарных вероятностей записывается в явном виде:
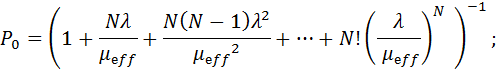 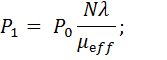
| (3.3) |
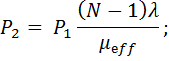 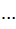 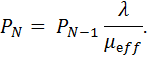
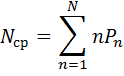 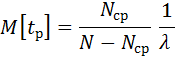 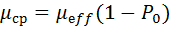
| (3.4) (3.5) (3.6) |
Следует отметить, что для расчета 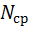 ,
, 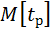 и
и 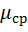 по формулам (3.4) - (3.6) кроме
по формулам (3.4) - (3.6) кроме 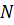 и
и 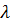 необходимо иметь значение параметра связи
необходимо иметь значение параметра связи 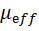 . Для его нахождения используется вторая агрегированная модель, АМ2.
. Для его нахождения используется вторая агрегированная модель, АМ2.
Модель АМ2. В модели АМ2 укрупненно представлена фаза терминалов. Ее влияние отражается с помощью обобщенного параметра 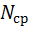 , представляющего собой среднее число заявок в системе «процессоры-каналы». В качестве состояния в момент
, представляющего собой среднее число заявок в системе «процессоры-каналы». В качестве состояния в момент 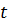 берется
берется 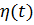 - число заявок на процессорной фазе. Структура модели АМ2 и граф переходов изображены на рис. 3.4 (а) и (б).
- число заявок на процессорной фазе. Структура модели АМ2 и граф переходов изображены на рис. 3.4 (а) и (б).
Обозначим
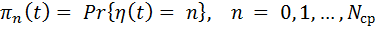
| (3.7) |
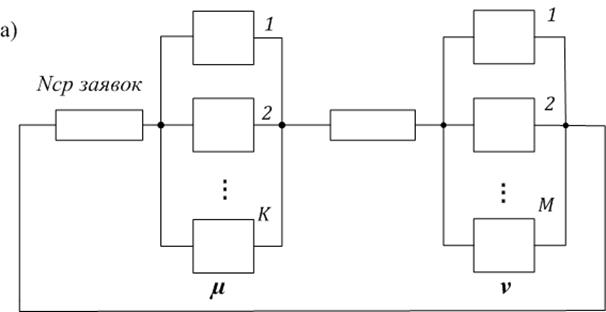
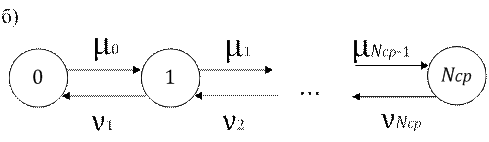
Рис. 3.4. Структура модели АМ2 (a) и граф переходов (б)
Расчетные соотношения таковы:
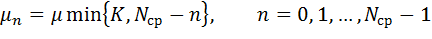 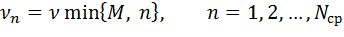
| (3.8) (3.9) |
Если обозначить через πn компоненту стационарного распределения вероятностей числа заявок на процессорной фазе, то
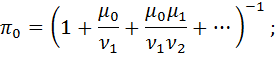
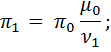
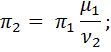 …
…
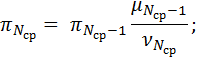
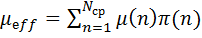 Ошибка в формуле! Как исправить? Ошибка в формуле! Как исправить?
| (3.10) (3.11) |
Для анализа АМ2, кроме 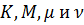 , надо знать
, надо знать 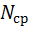 .
.
В рассмотренном варианте метода декомпозиции параметрами связи между агрегированными моделями АМ1 и АМ2 являются 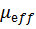 и
и 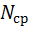 .
.
Таким образом, система уравнений (3.3) – (3.11) должна решаться совместно. Совокупность соотношений (3.3), (3.4) в сущности, представляет собой уравнение
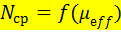
| (3.12) |
Совокупность соотношений (3.8) - (3.11) в сущности, представляет собой уравнение
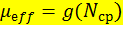
| (3.13) |
Подставляя (3.13) в (3.12), получаем уравнение
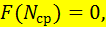 где где 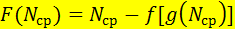 . .
| (3.14) (3.15) |
Уравнение (3.14) можно решать, например, методом половинного деления или методом перебора с переменным шагом, или методом простой итерации, взяв в качестве отрезка, на котором находится корень, отрезок 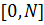
При 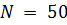 для решения уравнения (3.14) методом половинного деления потребуется 5 раз вычислить значение функции
для решения уравнения (3.14) методом половинного деления потребуется 5 раз вычислить значение функции 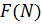 . Нетрудно видеть, что это составляет порядка 103 - 104 операций, что соответствует долям секунды (время одновариантного анализа) даже при использовании средних ЭВМ 70-х годов прошлого века. Поэтому такая декомпозиция легко допускает построение зависимостей выходных характеристик от параметров системы (многовариантный анализ).
. Нетрудно видеть, что это составляет порядка 103 - 104 операций, что соответствует долям секунды (время одновариантного анализа) даже при использовании средних ЭВМ 70-х годов прошлого века. Поэтому такая декомпозиция легко допускает построение зависимостей выходных характеристик от параметров системы (многовариантный анализ).
В рассмотренном варианте метода декомпозиции параметрами связи между агрегированными моделями АМ1 и АМ2 являются  и
и 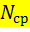 .
.
Итак. простая итерация. Nср0 = N/2. Подставляем в модель АМ2. Полученное  подставляем в модель АМ1. Получаем Nср1. После их сравнения подставляем Nср1 в модель АМ2. Получаем новое
подставляем в модель АМ1. Получаем Nср1. После их сравнения подставляем Nср1 в модель АМ2. Получаем новое  . При их близких значениях
. При их близких значениях