УДК:004.451:004.43
АРИФМЕТИЧЕСКИЕ СИСТЕМЫОГРАНИЧЕННОЙ РАЗРЯДНОСТИ/ТОЧНОСТИ
ЛюлюзовМалик Юсупович, магистрант 1-го курса направления 710400 «Программная инженерия», кафедра «Программное обеспечение компьютерныхсистем» (ПОКС), КГТУ им. И. Раззакова, (+996) 56-38-53. г.Бишкек, пр. Мира 66, e-mail:abdu.malik5660@gmail.com.
Тен Иосиф Григорьевич, к.т.н., профессор, заведующий кафедрой ПОКС, КГТУ им. И. Раззакова, (+996) 56-38-53. г.Бишкек, пр. Мира 66, e-mail:tenig@mail.ru.
Мусина Индира Рафиковна, к.т.н., доцент кафедры ПОКС, КГТУ им. И.Раззакова, (+996) 56-38-53. 720044, г.Бишкек, пр. Мира - 66, e-mail: musina-indira@yandex.ru
Аннотация
В данной статье рассматриваются основные причины появления ошибок, неизбежных при любых вычислениях на компьютере. Главное внимание уделено детальному изучению и наглядному представлению арифметических систем ограниченной разрядности/точности, которые используются в любых цифровых компьютерах. Предлагается решение проблемы определения требуемых характеристик процессора для успешной работы программы.
Ключевые слова: компьютерная арифметика, точность вычислений, разрядность процессора, числа с плавающей запятой.
Finite-precision arithmetic systems
Malik UsupovichLuluzov, First-year master student of Software Engineering (SE) Department, Kyrgyz State Technical University (KSTU) named after I. Razzakov, (+996) 56-38-53. 720044, Bishkek city, 66, prospect Mira, e-mail: abdu.malik5660@gmail.com.
IosifGrigorievich Ten, PhD, Professor, Head of SEDepartment, KSTU, named after I. Razzakov, (+996) 56-38-53. 720044, Bishkek city, 66, prospect Mira, e-mail: tenig@mail.ru.
Musina Indira Rafikovna, PhD, Associate Professor, SEDepartment,(+996) 56-38-53.720044, Bishkek city, KSTU named after I.Razzakov e-mail: musina-indira@yandex.ru.
Summary
The article discusses the main causes of the errors that are inevitable in any calculations on a computer. The main attention is paid to the detailed study and a clear presentation systems limited arithmetic word length /precision that is used in all digital computers. It proposed solution to the problem of determining the required processor performance to the success of the program.
Keywords: computer arithmetic, calculation accuracy, bit processor, a floating point number.
Введение
На сегодняшний день при решении любой задачи, требующей арифметических вычисленийна компьютере, пользователь сталкивается с двумя видами ошибок: ошибки входных данных (ошибки действий пользователя) и ошибки вычислений. И если на первый вид ошибок разработчикиникак повлиять не могут, то ответственность за появление ошибок второго вида полностью возлагается на них.Данная статья посвящена решению проблемы, связанной именнос ошибками вычислений.
Если исключить все ошибки разработчика, связанные с неверной реализацией алгоритма, то ошибки в вычисленияхмогут появляться из-за округления в самой системе, т.к. любая компьютерная система не может быть бесконечно точной. Причиной такого рода ошибок является ограничение памяти и разрядности процессора. К примеру, в обычной арифметике, между нулем и единицей существует бесконечное количество вещественных чисел, а компьютер из-за своей ограниченной памяти не может хранить и использовать такие числа. В таких случаях компьютеру приходится их округлять.Для представления таких чисел, была введена система чисел с плавающей запятой, что является компромиссом между точностью вычислений и скоростью работы.Число с плавающей запятой состоит из набора отдельных разрядов, условно разделенных на знак, порядок и мантиссу[1]. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой (рис. 1).
Рис.1. Представление числа с плавающей запятой.
Постановка задачи
Разработка любого программного обеспечения начинается с разработки технического задания (ТЗ). Кроме функциональных требований, в ТЗ должны быть представлены и нефункциональные требования, в которых одним из основных является требования к компьютеру (процессору). Большинство программистовне могут обоснованно предъявить требования к характеристикам hardware. Некоторые разработчики, пытаясь сэкономить средства заказчика, приводятв требованиях к hardware более слабые характеристики, тем самым подвергая рискам работу будущей системы.В то время как, другие завышают требования, вынуждая заказчиков приобретать более дорогие компьютеры с высокими характеристиками, в то время, как в этом нет никакой необходимости. Таким образом, возникает необходимость в программе, которая будет наглядно демонстрировать зависимость точности от разрядности процессора.
Разработка программы
Цель разработки программы - определить максимально возможную точность для разных процессоров. Эта программа позволит программистам в техническом задании правильно сформировать требования к характеристикам компьютера для достижения требуемой точности вычислений.
Для определения максимально возможной точности в программе пользователю будет необходимо лишь ввести некоторые исходные данные, такие как:
· β – основание исчисления. Основание определяет систему счисления разрядов. Математически доказано, что числа с плавающей запятой с базой β = 2 (двоичное представление) наиболее устойчивы к ошибкам округления, поэтому на практике встречаются только базы 2 и, реже, 10.
· t – параметр, характеризующий разрядность процессора,
· L – нижняя граница экспоненциального показателя,
· U – верхняя граница экспоненциального показателя.
Программа в качестве результатов выдает следующие параметры:
ü Любое число в системе с плавающей запятой представляется следующим образом:
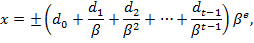
где
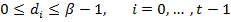
ü Количество всех чисел в системе с плавающей запятой, вычисляемое по формуле:
ü UFL – Уровень исчезновения разрядов:
ü OFL – Уровень переполнения разрядов:
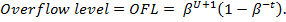
ü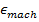 
–Machineprecision (машиннаяточность). Это - минимальный шаг от одного вещественного числа к другому. Перед вычислением значения 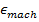необходимо определиться со способом округления чисел в системе с плавающей запятой. Существует два основных способа округления:
§ Chop – “Рубить” –«отрубает» правую часть вещественного числа, оставляя слева нужное количество символов.
§ Roundtonearest – “Округление до ближайшего”, является режимом по умолчанию и подходит для большинства применений, он обеспечивает наиболее точный результат.
После того, как определились с выбором способа округления, вычисляем значение 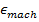. Для способа округления Chop, используем формулу [2]:
Для способа округления Roundtonearest, используем формулу[2]:
Выше представленные модели были реализованы в программе, разработанной специально для исследования зависимости точности от разрядности процессора. Программа разработана на языке C#в среде VisualStudio2013.
Результаты исследований
Для исследования зависимости точности вычислений от используемого процессора (процесса округления вычислений) с помощью разработанной программы использовались следующие значения (рис. 1):
Betta (β)= 2 – бинарная система исчисления;t= 3;
L (нижняя граница экспоненциального показателя) = -1;
U (верхняя граница экспоненциального показателя) = 1;
В качестве способа округления выбранRoundtonearest(округление до ближайшего).
После нажатия на кнопку Start программа вычислила:
UFL (Underflow Level) = 0.5;OFL (Overflow Level) = 3.5;E_mach (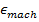)= 0,125;
AmountofPoints(Общее количество чисел в системе с плавающей точкой) = 25;
На графике, представленные на рисунке 1, изображены все точки, возможные при таких исходных данных. График показывает, что при разрядности процессора равной 3, нельзя получить, например, число 0,25 или 0,3. И если отнять от числа 3 число 0,75, то мы получим 2, т.к. в смоделированной системе чисел с плавающей запятой, числа 2,25 не существует.
На рисунке 3 представлены результаты работы программы при увеличении разрядности (t=4).В этом случае, благодаря увеличению точности, мы сможем получить число 2,25, если отнимем 0,75 от числа 3.
Рис.2.Результаты исследований приt=3.
График показывает, что с увеличением разрядности увеличивается точность вычисления, а также диапазон значений чисел и их количество.
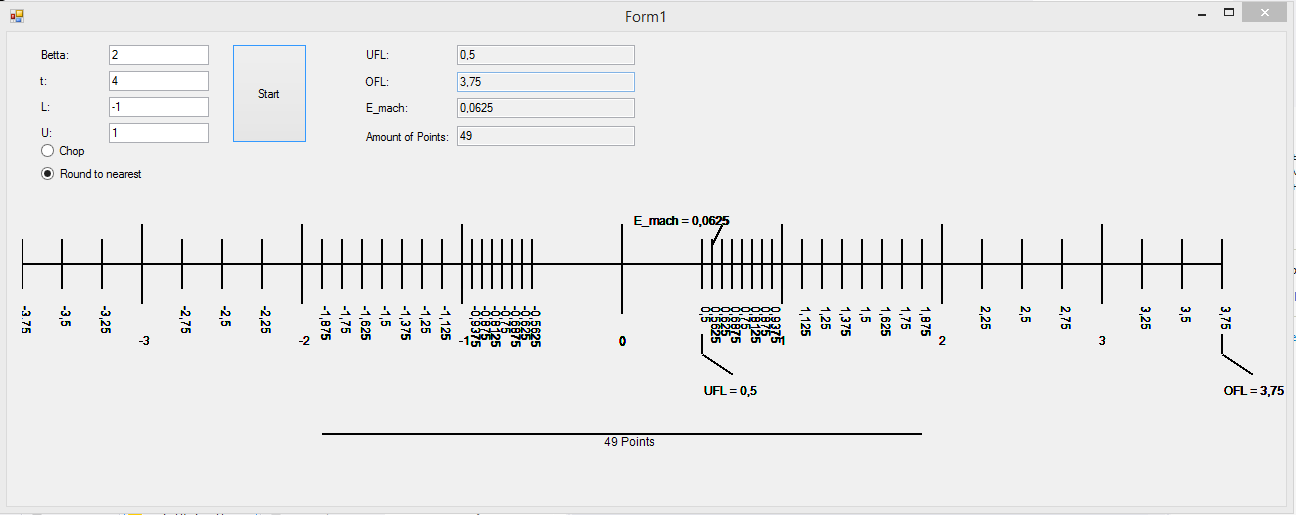
Рис.3.Результаты исследований приt=4.
Заключение
Были проведены исследования в области компьютерной арифметики, выявлены основные проблемы и на основе полученных данных была разработана программа, которая наглядно демонстрирует зависимость точности от разрядности процессора. С помощью данной программы можно определить максимально возможную точность для процессоров с разной разрядностью. Эта программа позволяет программисту в техническом задании правильно сформировать требования к характеристикам компьютера, чтобы достичь требуемой точности вычислений.
Литература
1. IEEE 754 - стандарт двоичной арифметикис плавающей точкой. https://www.softelectro.ru/ieee754.html.
2. Heath M.T. ScientificComputing.An Introductory Survey. Boston McGraw Hill, 1997 ISBN 0-07-027684-6.
References
IEEE Standard for Binary Floating-Point Arithmetic. (ANSI/IEEE Std 754-1985).
2. Heath M.T. ScientificComputing.An Introductory Survey. Boston McGraw Hill, 1997 ISBN 0-07-027684-6.