Занятие № 3
Пример 1. Пробу глины проанализировали в двух лабораториях и получили следующие значения содержания SiO2, %:
лаборатория № 1 (n = 5): 41,6; 41,9; 41,4; 41,3; 41,7;
лаборатория № 2: (m = 8): 41,1; 40,9; 41,3; 41,4; 42,1; 41,5; 41,4; 40,7.
Полагая, что содержание SiO2 подчиняются нормальному закону распределения, выяснить, можно ли считать равными оценки случайных погрешностей результатов анализа.
Введём выборочные данные в диапазоны А2:А6 и B2:B9, а тексты-метки в ячейки А1, B1, C2, C3, C4, C5, C6.
В ячейку D2 ввести формулу: =ДИСП.В(A2:A6). Получим значение исправленной выборочной дисперсии для лаборатории 1: 0,057.
В ячейку D3 ввести формулу: =ДИСП.В(B2:B9). Получим значение исправленной выборочной дисперсии для лаборатории 2: 0,018.
Так как D3 > D2, в ячейку D4 введём формулу = D3/ D2. Получим наблюдаемое значение критерия: 3,16.
Вычислим критические значения критерия. Функция F.ОБР.ПХ(вероятность;степени_свободы1;
степени_свободы2) возвращает обратное значение для F-распределения вероятностей.
Зададим уровень значимости α = 0,05. В ячейки D5 и D6 введём соответственно формулы: = F.ОБР.ПХ (0,05; 7; 4) и = F.ОБР.ПХ (0,025; 7; 4). Получим в ячейках D5 и D6 критическиезначения F кр.: 6,09 и 9,07.
Если в качестве альтернативной гипотезы рассматривается гипотеза H 1: D (Y)> D (X), то уровню значимости α = 0,05 и степеням свободы k 1 = 7 и k 2= 4 соответствует F кр.= 6,09. Так как F набл.< . F кр., то гипотеза H 0: D(X) = D(Y) принимается.
При альтернативной гипотезе H 1: D(Y) ≠ D (X)в качестве критического значения принимается F кр.= 9,07, также нет оснований отвергать нулевую гипотезу (3,16 < 9,07).
Вывод: результаты можно считать равноточными.
Для проверки гипотезы о равенстве дисперсий можно использовать функцию F.ТЕСТ(Массив 1, Массив 2), которая определяет расчётное значение уровня значимости p в случае двусторонней критической области.
Введём в свободную ячейку, например в D7, формулу:
=F.ТЕСТ(A2:A6; B2:B9). Получим результат: 0,28. (Уровень значимости для двусторонней критической области, а для односторонней - 0,14). Так как p > 0,05, то гипотеза H0 принимается на уровне значимости p.
Проверим нулевую гипотезу с помощью инструмента Пакета анализа «Двухвыборочный F-тест для дисперсии». Перейдём на вкладку Данные и в группе Анализ нажмём кнопку Анализ данных. В диалоговом окне Анализ данных выберем инструмент
«Двухвыборочный F-тест для дисперсии » и в окне диалога введём следующие значения:
Нажмём кнопку ОК и получим следующий результат:
В таблице результатов: df ‒ число степеней свободы; 
. Так как 
, то альтернативная гипотеза формулируется как H 1: D(X) < D(Y) и строится левосторонняя критическая область в интервале (0; 0,16). Так как F кр.= 0,32. F набл> F кр., следовательно наблюдаемое значение критерия не попадает в критическую область, и нулевую гипотезу следует принять. Значение левосторонней критической точки (показатель F критическое одностороннее) рассчитывается по формуле: = F.ОБР (0,05;4; 7).
Пример 2. Была измерена производительность шести химических аппаратов в кг/ч. Результаты измерений:
I: 14,0; 14,5: 13,7; 12,7; 14,1;
II: 14,1; 10,1; 14,7; 13,7;
III: 14,0; 12,3; 12,8; 11,0; 13,1;
IV: 14,5; 14,2; 15,0; 14,7; 13,5;
V: 12,5; 12,3; 11,5; 12,9;
VI: 14,0; 14,0; 13,5; 14,7.
На уровне значимости α = 0,05 проверить гипотезу о равенстве дисперсий.
Введём выборочные данные в диапазоны А3:F7, а тексты-метки в ячейки диапазона А2:F2.
В ячейки диапазона А8:F8 введём объёмы выборок n 1, …, n 6.
В ячейку A9 введём функцию =ДИСП.В(A3:A7). В ячейке A9 появится значение исправленной выборочной дисперсии 
. Протянем формулу до ячейки F9, скорректировав диапазоны,и получим значения 
,…, 
.
В ячейку A10 введём формулу =(A8-1)*A9 и затем с помощью маркера заполнения скопируем эту формулу в ячейки B10:F10. В ячейках диапазона A10:F10 появятся результаты вычислений по формуле 
.
В ячейку A11 введём формулу =LOG10(A9) и с помощью маркера заполнения скопируем эту формулу в ячейки B11:F11. В диапазонt A11:F11 появятся результаты вычислений по формуле 
.
В ячейку A12 введём формулу =(A8-1)*A11 и затем с помощью маркера заполнения скопируем эту формулу в ячейки B12:F12. В диапазоне A12:F12 появятся результаты вычислений по формуле 
.
В ячейку A13 введём формулу =1/(A8-1) и скопируем её с помощью маркера заполнения в ячейки B13:F13. В диапазоне A13:F13 появятся результаты вычислений по формуле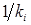 
.
В ячейки диапазона G1:G13 введём информационные метки.
В ячейки диапазона H1:H13 введём формулы, реализующие заключительный этап вычислений:
| Ячейка | Формула | Ячейка | Формула |
| H1 | =СУММ(A8:F8) | H8 | =H7-1/(H1-6) |
| H2 | =СУММ(A10:F10) | H9 | =H8/3/5 |
| H3 | =H2/(H1-6) | H10 | =1+H9 |
| H4 | =(H1-6)*LOG10(H3) | H11 | =H6/H10 |
| H5 | =СУММ(A12:F12) | H12 | =ХИ2.ОБР.ПХ(0,05;5) |
| H6 | =2,303*(H4-H5) | H13 | =ХИ2.РАСП.ПХ(H11;5) |
| H7 | =СУММ(A13:F13) |
Пример 3. Была измерена производительность шести химических аппаратов в кг/ч. Результаты измерений:
I: 14,0; 14,5: 13,7; 12,7; 14,1;
II: 14,1; 10,1; 14,7; 13,7; 14,0;
III: 14,0; 12,3; 12,8; 11,0; 13,1;
IV: 14,5; 14,2; 15,0; 14,7; 13,5;
V: 12,5; 12,3; 11,5; 12,9; 12,8;
VI: 14,0; 14,0; 13,5; 14,7; 13,6.
На уровне значимости α = 0,05 проверить гипотезу о равенстве дисперсий.
Введём данные и рассчитаем исправленные выборочные дисперсии в диапазоне А8:F8.
В ячейке I3 найдём значение G набл, найденное с помощью формулы =B8/СУММ(А8:F8), а в ячейке I5 – критическое значение g(0,05;6;4)=0,4803 этой статистики, вычисленное с помощью формулы = БЕТА.ОБР(1 – I4/I1;I2 /2; I2 * (I1 − 1)/2).
Полученный результат (G набл >gкрит) свидетельствует о том, что гипотеза о равенстве дисперсий противоречит реальным данным.
Пример 4. Были измерены диаметры валиков, изготовленных на двух агрегатах, в мм:
I агрегат: 180; 182; 184; 185; 182; 179; 185; 181; 183; 179
II агрегат: 183; 190; 184; 188; 182; 183; 189; 183; 185; 184;
183; 185.
Известно, что размер диаметров имеет нормальный закон распределения с дисперсиями D (X)= 5 мм2 для аппарата І и D(Y) = 7 мм2 для аппарата ІІ. Можно ли на уровне значимости α = 0,05 объяснить различие выборочных средних случайными причинами?
Введём исходные данные в диапазоны А2:А11 и B2:B13 и тексты-метки в ячейки А1, B1, C2, C3, C4, C5, C6, C7, C8, C9, C10. В ячейки D2 и D3 введём значения дисперсий, а в ячейки D4 и D5 ‒ объёмы выборок.
Вычислим средние значения для выборок. В ячейку D6 введём формулу =СРЗНАЧ(A2:A11), а в ячейку D7 ‒ =СРЗНАЧ(B2:B13). Получим значения 182 и 184,9167.
Рассчитаем наблюдаемое значение критерия. Для этого в ячейку D8 введём формулу: =(D6-D7)/КОРЕНЬ(D2/D4+D3/D5). Получим результат: -2,802243.
Для вычисления критического значения при конкурирующей гипотезе H 1: M (X) < M (Y) в ячейку D9 введём формулу: = НОРМ.СТ.ОБР(1-0,05). Получим результат: 1,644854.
Так как ½ Nнабл. ½> Nкр., то нулевую гипотезу о равенстве математических ожиданий следует отвергнуть.
При альтернативной гипотезе H 1: M (X) ≠ M (Y) уровню значимости α соответствует двусторонняя критическая область. Критическое значение вычисляется с помощью функции: НОРМ.СТ.ОБР(1-0,05/2). Введём формулу в ячейку D10 и получим результат: 1,959964. Так как ½ Nнабл. ½> Nкр., то нулевую гипотезу о равенстве математических ожиданий следует отвергнуть и в этом случае, то есть нельзя объяснить различие выборочных средних случайными причинами.
Для проверки гипотезы при известных дисперсиях можно использовать инструмент Пакета анализа «Двухвыборочный z-тест для средних ».
В диалоговом окне инструмента введём следующие данные:
Получим результат:
Если выборки имеют большой объём (>30) и независимы, то критерий для проверки о равенстве средних можно применять также в следующих случаях: генеральные совокупности распределены нормально, а дисперсии их неизвестны; генеральные совокупности не распределены нормально и дисперсии их неизвестны. При этом вместо неизвестных дисперсий используются исправленные выборочные дисперсии.
Пример 5. Проверить гипотезу о равенстве средних для данных примера 1.
В предположении, что дисперсии генеральных совокупностей одинаковы, требуется проверить гипотезу H 0: M (X) = M (Y), то есть необходимо установить, значимо или незначимо различаются статистические оценки 
и 
, вычисленные по независимым выборкам.
Для проверки гипотезы воспользуемся стандартной функцией MS Excel ТТЕСТ, которая определяет вероятность, соответствующую найденному значению критерия. Аргументы функции: Массив1 – первый набор данных; Массив2 – второй набор данных; Хвосты – число хвостов распределения (1 или 2). Если Хвосты равно 1, то функция определяет уровень значимости для односторонней доверительной вероятности. Если Хвосты равно 2, то функция определяет уровень значимости для двусторонней доверительной вероятности. Тип – вид исполняемого теста: 1 – парный; 2- двухвыборочный с равными дисперсиями (гомоскедатический); 3 – двухвыборочный с неравными дисперсиями (гетероскедастический).
В ячейку В30 введём формулу:
=TТЕСТ(A2:A12;B2:B11;2;2). Получим результат:.
Так как 
, то нет оснований отвергать нулевую гипотезу. Уровень значимости также больше 0,05.
Проверим гипотезу с использованием инструмента Пакета анализа Двухвыборочный t-тест с одинаковыми дисперсиями.
В таблице объединённая дисперсия рссчитывается по формуле:
Замечание. В случае, если гипотеза о равенстве дисперсий не подтверждается, то для проверки гипотезу о равенстве средних следует использовать инструмент Двухвыборочный t-тест с разными дисперсиями.
Пример 6. Необходимо сравнить работу двух измерительных приборов, используемых для проверки размеров деталей. Из партии была сделана случайная выборка объёмом n = 10 и проведены замеры обоими приборами. Результаты замеров:
Прибор А: 76,1; 76,2; 76,0; 76,04; 76,10; 76,08; 76,18; 76,02; 76,12; 76,06.
Прибор Б: 76,2; 76,0; 76,25; 76,02; 76,18; 76,06; 76,04; 76,25;
76,00; 76,10.
Необходимо на уровне значимости α = 0,01 определить, имеются ли существенные различия между приборами А и В.
Введём исходные данные и для проверки гипотезы воспользуемся функцией MS Excel TТЕСТ. В качестве аргумента Тип укажем 1 – парный тест.
В ячейку B13 введём формулу: =ТТЕСТ (A2:A11;B2:B11;2;1) и получим значение двусторонней вероятности значимости: 0,68442036.
В ячейку B14 введём формулу: =ТТЕСТ (A2:A11;B2:B11;1;1)
и получим значение односторонней значимости: 0,34221018.
В Пакете анализа MS Excel для проверки гипотезы о равенстве средних для двух зависимых выборок используется инструмент «Парный двухвыборочный t-тест для средних». В нём не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные. Парный тест используется, когда имеется естественная парность наблюдений в выборках.
Введём следующие параметры.
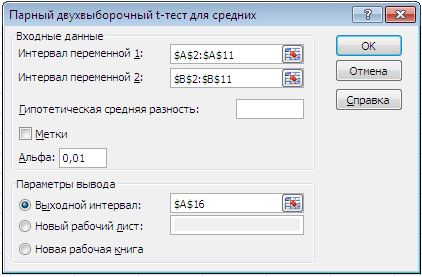
Вывод: так как ½ Tнабл. ½< Tкр., то нулевую гипотезу следует принять.
В итоговой таблице содержится значение выборочного коэффициента корреляции Пирсона, которое позволяет оценить степень зависимости выборок.