| Выполнила: студентка 3 курса группы МО-15 ИМИ СВФУ Николаева Валерия Васильевна Руководитель работы: Бубякин Игорь Витальевич, доцент кафедры алгебры и геометрии ИМИ СВФУ | |
| Работа проверена ___ ______________ 2018 г. Оценка __________________ _________________ И.В. Бубякин |
Якутск – 2018
ОГЛАВЛЕНИЕ
Введение.......................................................................................................................3
1 Лексикографическая последовательность элементов треугольника...................5[A1]
1.1 Лексикографическое изложение конструктивных задач геометрии треугольника.………….…...…………………………………………………...........5
1.1.1 Предмет и значение теории геометрических построений…….........5
1.1.2 Характеристика сборников конструктивных задач………........…...8
1.1.3 О лексикографическом принципе изложения……………........……9
1.2 Список Верника...……………………………………………..……....…12
2Изложение конструктивных задач........................................................................15
Заключение.................................................................................................................18
Список использованной литературы.......................................................................19[A2]
ВВЕДЕНИЕ
В 1937 году в журнале «Математика в школе» №5 и №6 была опубликована пространная статья В.Б. Фурсенко[8] о построении треугольника по трём элементам.В этой статье Фурсенко расположил все задачи на построение треугольника в лексикографическом порядке, решил все задачи, которые имеют решение и перечислил все задачи, которые решения не имеют.
В педагогической практике известны задачи на восстановление треугольника по трём заданным точкам. В 1982 году Уильям Верник [11] так же, как и Фурсенко в 1937-ом, составил лексикографический список задач на восстановление треугольника.
|
|
После чего он составил список, который называется список Верника, в котором из 139 принципиально различных задач лексикографического списка имеют решение чуть больше половины – 72 задачи. Интересно, что сам Верник, не исследовал задачи на неразрешимость, а нашел решение только 65 задач.
Цель моего исследования – это свежий взгляд на использование научных данных Фурсенко и Верника в методике преподавания. Она нуждается в глубоком изучении теоретического материала, его осмыслении и дальнейшем развитии.
В наше «компьютерное» время, существует много разных программ, которые способны решить геометрические задачи легкого уровня без проблем[A3]. Назревает вопрос«Как создать новую методику решения задач с помощью программирования, основываясь на трудах предыдущих математиков[A4]?».
Актуальна еще проблема школьной программы. Фурсенко выявил проблему в обучении школьников в своей статье, но это осталось незамеченным. И мы до сих пор мечемся из стороны в сторону, чтобы понять «Как учить?».
Задачи исследования: изучение научной и методической литературы, анализ научных статей, исследование задач конструктивной геометрии треугольника на основе лексикографической последовательности его элементов.
Объектом исследования данной работы является треугольник.
Методы исследования: анализ теоретического материала и решение задач.
Новизна работы: Возможно, создать что-то основанное на трудах Фурсенко, используя современные технологии и современную методику преподавания – это может являться новизной, но в данной работе мы рассматриваем только идеи, рассуждения, анализ теории и поэтому пока что новизна не установлена.
|
|
Курсовая состоит из введения, двух глав, заключения и списка использованной литературы.
В первой главе рассматривается такое понятия как предмет теории геометрических построений, значение теории геометрических построений, разрешимость конструктивных задач, характеристика сборников задач, методика решения задач, Список Верника.
Во второй главе проведен краткий анализ решенных конструктивных задач геометрии треугольника основанных на лексикографической последовательности его элементов.
1 ЛЕКСИКОГРАФИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ЭЛЕМЕНТОВ ТРЕУГОЛЬНИКА
1.1 Лексикографическое изложение конструктивных задач геометрии треугольника
1.1.1 Предмет и значение теории геометрических построений
Содержание теории геометрических построений, как известно, складывается главным образом из описании методов геометрических построений (инструменты и способы их применения для решения тех или иных задач). Наиболее развитой является теория методов геометрических построений с применением циркуля и линейки. Главной задачей теории геометрических построений является описание методов построения. В связи с нею рассматривается еще ряд вопросов. Прежде всего возникает вопрос об исследовании области применения средств построения (инструментов), т. е. выяснения того, какие задачи можно решать каждым из них в отдельности, какие же помощью нескольких. Непосредственным развитием этого вопроса являются доказательством невозможности решения некоторых задач при пользовании определенными инструментами. Ф. Энрикес[9] высказал следующее положение: «не существует абсолютно неразрешимых задач, не есть лишь относительно неразрешимые». Нас будет интересовать вопрос о том, какие задачи неразрешимые циркулем и линейкой.
|
|
Теория геометрических построений рассматривает также вопрос о классификации геометрических задач. Если в основу классификации положен принцип свойств искомой фигуры, то задачи распределяются на визуальные, метрические, проективные. Если в основу классификации кладутся те уравнения, к которым приводится решения задач, то говорят о задачах трансцендентных и алгебраических первой, второй, третьей, четвертой и высших степеней. В связи с этим можно классифицировать задачи по роду кривых, которые вычерчиваются при решении задач, а следовательно, и по роду инструментов, при помощи которых задача может быть решена: говорят о задачах из геометрии эллиптического циркуля и т. п. Наконец, в основу классификации могут быть положены сами искомые фигуры, т. е. можно говорить о задачах на построение треугольников, параллелограммов, окружностей т.п. Именно, классификация по этому признаку является наименее совершенной, в которых задачи распределились по данному признаку.
Значение теории геометрических построений не всегда правильно понимается.Элементарная формулировка конструктивных задач и то обстоятельство, что решение их требует обычно некоторой сообразительности, нередко возводится в основной признак, характеризующий значение геометрических построений. Геометрические построения рассматривают только как средство развития сообразительности учащихся средней школы, а отсюда вытекает либо то, что подбор задач, предлагаемых для решения в средней школе, носит случайный характер, либо то, что задачи на построение по причине их относительной трудности вовсе исключается из школьной практики.
Таким образом, непонимание истинного значения геометрических построений, сведения их на ряд занятых головоломок, обуславливает в значительной мере то, что место, занимаемое ими в школьном преподавании, все ещеостается не определенным, и официальная программа средней школы высказывается по этому вопросу также еще не вполне внятно. Прежде всего можно упомянуть о роли геометрических построения в решении некоторых экстремальных задач, разыскании некоторых экстремальных свойств изучаемой функции. Для этого достаточно придать геометрический смысл изучаемой зависимости и выполнить построение, отвечающее указанному геометрическому смыслу. Соответственное экстремальное свойство обычно немедленно вытекает из условий, при которых выполнимо данное геометрическое построение.
Решение нелинейных систем уравнений, приводящее к громоздким вычислениям, если решение проводится алгебраическим методами, путем методов геометрических построений во многих случаях значительно упрощается.
Большое значение имеют геометрические построения при решении вопросов об условиях равенства и подобия геометрических фигур. Построив изучаемую фигуру, нетрудно вывести из анализа данных, необходимых для построения и исследования количества получаемых решений, условия равенства изучаемых фигур. Равным образом, отбросив некоторое число линейных данных, нетрудно установить и условия подобия фигур.
Геометрические построения представляют мощное орудие математического исследования.
Неразрешимость некоторых задач теории геометрических построений послужила поводом глубочайших исследований, посвященных выяснению природы числа и явилась толчком к развитию тонкого и сложного математического аппарата.
В современном своем положении теория геометрических построений теснейшим образом связана с теорией Галуа. Вопросом о возможности того или иного построения равносилен вопросу о разрешимости известного класса уравнений в квадратных радикалах, ответ на который может дать теория Галуа. С другой стороны, если установлена возможность геометрического построения, отвечающего известному классу уравнения, то этим самым решен вопрос о разрешимости данного класса уравнений в квадратных радикалах, что не менее важно, так как применение теории Галуа к уравнениям высших степеней практически почти невозможно.
Другой путь решения вопроса о возможности того или иного построения, требует обширных исследований в области аналитической геометрии.
1.1.2 Характеристика сборников конструктивных задач
Как известно, существует достаточное количество всякого рода задачников, содержащих задачи на построение, а нередко и их решения. Эти задачники можно подразделить на три группы. Первая группа содержит задачи, распределенные по их «материальному» содержанию (задачи на построение отрезков, углов, треугольников, четырехугольников, кругов и т. п.). Вторая группа содержит задачи, распределенные по методам решения (метод геометрических мест, подобия, алгебраической и т. п.). Наконец, третья группа содержит задачи, распределенные по так называемому «педагогическому» принципу, т.е. в полном хаосе, так как в области теории геометрических построений нам не пришлось найти ни одной серьезной, на одной заслуживающей внимания методической статьи, в которой приводились бы научно обоснованные принципы установления порядка постепенного прохождения зада на построение.
Надо отметить, что ни одна из приведенных нами групп (о третьей говорить не приходиться) с точки зрения выдержанности принципа, положенного в основу составления задачника, не может быть признана удовлетворительной.
Если в основу положено материальное содержание задачи, то этот принцип не выдерживается в силу того, что авторы стремятся приноровить задачник к потребностям средней школы, где развивающийся курс геометрии предоставляет все новые методы для решения задач с материальным содержанием, уже рассмотренным ранее. В результате этого получается своеобразный концентризм и мы находим, например, три главы о построении треугольников (в элементарных построениях, после учения о подобии и после учения о площадях).
В геометрии можно указать очень хорошие задачи, которые решаются семью способами и даже более, и это ничуть не мешает задаче быть в том или другом отношении типичной. Напротив, появление нескольких решений одной задачи дает лишний шанс как автору задачника, так и преподавателю и ученику обнаружить зоркость и находчивость в выборе простейшего способа и умение сравнить методы в отношении простоты и типичности решения. Само собою разумеется, что учащихся должна быть предоставлена полная свобода в выборе решения-опыт показывает, что такая свобода вполне совместима с изучением методов.
Нам представляется, что единственно правильным распределением планиметрических задач на построение было бы таким:
1) элементарные построения;
2) небольшое количество подробно разобранных задач, расположенных по методам решения (не свыше пяти-шести на каждый метод);
3) задачи на построение треугольников по его элементам;
4) задачи на построение четырехугольников по его элементам;
5) задачи на построение кругов, касательных к прямым или данным кругам;
6) задачи на построение правильных многоугольников;
7) задач на рассечение площадей;
8) задачи положения.
Задачи внутри отделов 3-8 должны быть расположены лексикографически.
1.1.3 О лексикографическом принципе изложения
Прежде всего несколько слов о принятых в данной работе обозначениях.
Таблица 1 – Обозначения треугольника
| Элементы треугольника | Обозначения |
| Стороны треугольника | a, b, c |
| Противолежащие углы треугольника (так же обозначены его вершины) | А, В, С |
| Соответственные высоты | 
|
| Соответственные медианы | 
|
| Соответственные биссектрисы |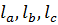 
|
| Радиус описанного круга | R |
| Радиус вписанного круга | r |
| Радиусы вневписанных кругов, касающихся соответственно сторон a,b,c | 
|
| Периметр треугольника | 2 p |
| Площадь треугольника | ∆=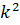 
|
Лексикографическая последовательность установлена следующая:
a, b, c,A,B,C, 
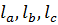, ,R,r, ,2p, ∆.
В данной статье рассматривается только остроугольные разносторонние треугольники, причем данный угол всегда предполагается острым.
Решение геометрической задачи склонны распределять на отдельные стадии. Например, Д. Гика [3]усматривает в решении конструктивной задачи пять стадий:
1) предположить задачу решенной и составить чертеж (гипотеза решения)
2) рассмотреть по чертежу, какие части фигуры даны, какие требуются найти и какая существует зависимость между искомыми данными на основании, известных теорем (анализ)
3) пользуясь зависимостью между искомыми и данными, найти искомые по данным (построение)
4) доказать, что найденные части фигуры удовлетворяют условия задачи (синтез)
5) рассмотреть, сколько задач имеет решений и определить условия их возможности (исследование)
Адлер [1]усматривает четыре стадии:
1) анализ геометрической задачи на построение,
2) выполнение построения,
3) доказательство правильности решения,
4) исследование
Основных методов, применяющихся при построении треугольников, имеется четыре.
Алгебраический метод.Этот метод является наиболее мощным. Сущность его заключается в том: что величину, определяющую искомый результат, а затем строят полученное алгебраическое выражение. Нередко при этом в полученное выражение входят тригонометрические функции. Если полученное выражение является неприводимым уравнением степени, неравной 2!, то данная задача неразрешима.
Будучи самым мощным, т.е. почти всегда приводящим к цели, алгебраический метод имеет тот недостаток, что мы по необходимости вводим в чертеж посторонние линии, чем затемняется геометрический смысл полученного решения.
Метод построения по частям. Этот второй по силе метод заключается в том, что задачу стараются свести к элементарным построениям или к ранее решенным задачам (последнее возможно при их лексикографическом расположении). Нередко при этом вращения, перекладывания или параллельного перенесения в другую, построение которой или части которой известны.
Метод геометрических мест.Этот метод слабее двух описанных выше, однако, применяется от также довольно часто. Метод заключается в том что данную задачу стараются свести к определению некоторой точки, определяемой двумя условиями, вытекающими из условий задачи. Если отбросить одно из этих условий, то второму будет удовлетворять бесчисленное множество точек, расположенных на некотором геометрическом месте. Если же отбросить второе условие вернуться к первому, то также получится некоторое геометрическое место. Каждая их точек пересечения этих двух геометрических мест удовлетворяет требования задачи.
Метод подобия. Наиболее слабым методом, применяющимся в нашей работе весьма ограниченно (главным образом, в тех задачах, является метод подобия. Сущность его заключается в том, что сначала строят фигур, подобную данной, а затем увеличивают или уменьшают ее в требуемом отношении. Метод подобия сокращено обозначается нами буквой (П).
В статье Фурсенко[8]рассмотрены все случаи построения остроугольного треугольника по трем его элементам, а следовательно работа автора заключалась, в том, что он, во-первых, составил из данных 22 элементов треугольника все возможные комбинации по три; во-вторых, удалил из этих 1540 комбинаций все тождественные. Это оказалось возможным благодаря применению лексикографического метода, т. е. установлению определенной иерархии между элементами треугольника и последующему расположению всех трех элементов по нисходящим степени этой иерархии.
В-третьих, был рассмотрен вопрос о том, какие из оставшихся 350 троек дают комбинации элементов, достаточные для построения треугольника циркулем и линейкой, что потребовало (исключая очевидные случаи, известные из школьного курса) исследования около 300 уравнений на их приводимость.
В-четвертых, осталось решить те задачи, которые допускают решение. Владея алгебраическими решениями всех 350 задач, автор, тем не менее, старался привести для разрешимых задач решение геометрическое или указать, по крайней мере, путь геометрического решения, следуя которому можно освободить чертеж от отрезков, посторонних геометрической сущности задачи, но которые необходимо возникают, если получается квадратное или биквадратное уравнение с более или менее сложными коэффициентами. Однако, не везде автору удалось это сделать и существующие задачники очень мало могли ему в этом помочь.
1.2 Список Верника
В статье Верника [11]было предложено рассмотреть задачу о восстановлении треугольника по трем точкам из следующих 16 (конечно же, многие подобные задачи рассматривались задолго до появления статьи):
A, B, C, O – вершины треугольника и центр описанной окружности;
, 
, 
, G – середины сторон треугольника и центр масс;
, 
, 
, H – основания высот треугольника и ортоцентр;
, 
, 
, I – основания биссектрис треугольника и центр вписанной окружности.
При таком подходе возникает 139 принципиально различных задач (например, из трех вариантов A, B, G; B, C, G; A, C, G естественно оставить только один). В некоторых тройках положение одной точки определяется по положению двух других. Например, таким свойством обладает тройка A, B, . Такие случаи помечены буквой R (redundant), задача о восстановлении треугольника для них не имеет однозначного решения. В некоторых тройках присутствует более слабая зависимость. Например, точки A, B, O не могут располагаться произвольно (точка O должна лежать на серединном перпендикуляре к отрезку AB). В зависимости от их взаимного расположения задача либо не имеет решения, либо имеет бесконечно много решений. Такие тройки помечены буквой L (locus– dependent). Разрешимые задачи имеют статус S (solvable), неразрешимые – U (unsolvable). Пустое место означает, что ответ насегодняшний день не известен.
По статье Верника, исследования провел преподаватель Хабаровского института прикладной математики ДВО РАН, Алексей Устинов. Тщательно изучив работу Вильяма Верника, он написал научную статью, которая называется «Можно ли построить треугольник по основаниям биссектрис?». [7]
Он рассуждает о нерешенных задачах и утверждениях, к которым они приводят, также раскрывает решения тех или иных задач черезнесколько теорем. Вот изначальный список Верника из его оригинальной статьи. [11]
Рисунок 1 – Список Верника(оригинальный вариант)
2 ИЗЛОЖЕНИЕ КОНСТРУКТИВНЫХ ЗАДАЧ
Двадцать один элемент лексикографической последовательности позволяет сформулировать 
= 1330 вариантов постановки задачи на построение треугольника по трем его элементам.
Поскольку любая задача на построение треугольника по трем его элементам допускает либо один вариант формулировки, либо три варианта, либо шесть, то указанные 1330 вариантов позволили выделить 293 различные задачи, из которых 178 оказались разрешимыми, а 115 – неразрешимыми или неопределенными.
Таблица 1 –Распределение элементов треугольника по базовым и дополнительным задачам[A5] (*с дополнительным элементом)
| № | Элемент треугольника сторона | БЗ | ДЗ* | Всего |
| угол | ||||
| высота | ||||
| медиана | ||||
| биссектриса | ||||
| радиус описанной окружности радиус вписанной окружности | ||||
| периметр |
a, b, c,A,B,C, , ,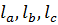R,r, ,2p.
Данная последовательность понимается как условный алфавит, предопределяющий порядок представления задач данного пособия. В частности, в первую очередь исчерпываются задачи, в которых дана хотя бы одна сторона треугольника, и т.д.
В статье Фурсенко существует 178 различных разрешимых задач, которые были исправлены, рассмотрены с другой стороны в 2015 году В.И.Голубевым, Л.Н.Ерганжиевой и К.К.Мосевичем, и была выпущена книга[4], где представлены все возможные построения треугольника по трем его элементам. Приводятся решения задач, сформулированных в многочисленных пособиях по элементарной геометрии. Также составлен список разрешимых и неразрешимых(неопределенных) задач, количество которых равно 176.
Так же как и Голубев, Ерганжиева и Мосевич, Алексей Устинов, преподаватель из Хабаровского отделения прикладной математики провел исследование глубже в учениях Уильяма Верника и добился немалых результатов, достигнув новых решений неопределенных задач. (см.рис.2) Он вывел немало теорем и лемм, следующих из решений задач. По некоторым тройкам точек из списка Верника возможно однозначное восстановление треугольника с помощью циркуля и линейки, по другим же тройкам однозначное восстановление невозможно. Кроме того, существуют другие тройки точек, не из списка Верника, при рассмотрении которых тоже получаются интересные задачи на построение.
В 2017 году студенты Агафонкин Григорий Андреевич и Веселова Варвара Алексеевна напечатали проектную работу «Восстановление треугольника по трем точкам». Основываясь на учениях Верника, они создали подборки наиболее интересных задач с наглядными иллюстрациями, а также навигатором используемым теоремам и методам. Они продолжают изучение и их исследование еще на стадии осмысления.
Рисунок 2 – Список Верника(дополненная Устиновым)
ЗАКЛЮЧЕНИЕ[A6]
В ходе написания курсовой работы, мы нашли новые статьи на данную тематику, сделали анализ их работы, также исследовали задачи конструктивной геометрии треугольника на основе лексикографической последовательности его элементов.
Данная работа дает краткий обзор основных научных статей на тему «Лексикографическая последовательность элементов треугольника», которая имеет важное место в геометрии треугольника. Исследование показало, что до сих пор, люди, интересующиеся углубленно геометрией треугольника пытаются найти решение тех или иных задач, основываясь на учениях Верника и Фурсенко. Этой теме есть куда развиваться[A7], и она не стоит на месте.
Список использованной литературы
[1] Адлер, А. Теория геометрических построений / А. Адлер – Л., Учпедгиз, 1940. – 232 с.
[2] Александров, И.И. Сборник геометрических задач на построение / И.И. Александров. –Учпедгиз, 1950. – 176 с.
[3] Гик, Д. Элементы геометрии, курс средних учебных заведений / Д. Гик –Москва: М.Д. Наумов, 1894. –250 с.
[4] Голубев, В.И. Построение треугольника / В.И. Голубев, Л.Н. Ерганжиева, К.К. Мосевич; – М.:БИНОМ. ЛЗ, 2015. –4-е изд. – 251 с.
[5] Куланин, Е.Д. Геометрия треугольника в задачах / Е.Д. Куланин, С.Н. Федин;– Мин. нар. Образования РСФСР, НИИ школ, 1990. – 144 с.
[6] Шлярский, Д.О. Избранные задачи и теоремы элементарной математики. Геометрия (планиметрия) / Д.О. Шлярский, Н.Н. Ченцов, И.М. Яглам;–М., Наука, 1976. – 384 с.
[7] Устинов, А.В. Можно ли построить треугольник по основаниям биссектрис? / А.В. Устинов // «Потенциал»: Математика, Физика, Информатика – 2013. – №10 – С. 41-[A8] 50.
[8] Фурсенко, В.Б. Лексикографическое изложение конструктивных задач геометрии треугольника / В.Б. Фурсенко // Математика в школе. –1937. – №5. –C. 6-35.
[9] Энрикес, Ф. Вопросы элементарной геометрии / Ф. Энрикес // СПБ, 1913. – С. 10-16.
[10] Meyers, L.F. Update in William Wernick’s “Triangle Constructions with Three Located Points” / L.F. Meyers // Math.Mag. –1996. – №69– С. 46-49.
[11] Wernick, W.Triangle Constructions with Three Located Points. / W. Wernick // Math.Mag. – 1982. – №55–С. 227-230.
[A1]многолочие
[A2]многоточие
[A3]Нет точки
[A4]Здесь должен стоять знак вопроса
[A5]отступ
[A6]по середине
[A7]нет запятой
[A8]дефис