РОЛЬ ВРЕМЕНИ В ИМИТАЦИОННЫХ МОДЕЛЯХ
План лекции
Масштабы времени
2. Способы управления модельным временем
Масштабы времени
Имитационный эксперимент представляет собой наблюдение за поведением системы в течение некоторого промежутка времени. Однако, далеко не во всех испытаниях фактор
времени играет ведущую роль, а в некоторых и вообще может не рассматриваться.
Например, при вычислении площади круга полученный результат
не зависит от того, сколь долго мы будем «бомбить» квадрат случайным и точками и исключать не принадлежащие кругу точки. Но значительно больше таких за-
дач, в которых оценка эффективности моделируемой системы напрямую связана с
временными характеристиками ее функционирования. К ним относятся, например,-
напримернннннндддд задачи по оценке производительности, некоторые задачи по оценке на-
дежности, качества распределения ресурсов, а также все задачи, связанные с иссле-
дованием эффективности процессов обслуживания. Характерной особенностью
большинства практических задач является то, что скорость протекания рассматри-
ваемых в них процессов значительно ниже скорости реализации модельного экспе-
римента. Например, если моделируется работа авторемонтной мастерской в тече-
ние недели, вряд ли кому-то придет в голову воспроизводить этот процесс в модели
в таком же масштабе времени.
С другой стороны, даже те имитационные эксперименты, в которых временные
параметры работы системы не учитываются, требуют для своей реализации опре-
деленных затрат времени работы компьютера.
В связи с этим при разработке практически любой имитационной модели и пла-
нировании проведения модельных экспериментов необходимо соотносить между
собой три представления времени:
|
|
- реальное время, в котором происходит функционирование имитируемой
системы;
- модельное (или, как его еще называют, системное} время, в масштабе которо-
го организуется работа модели;
- машинное время, отражающее затраты времени ЭВМ на проведение ими-
тации.
С помощью механизма модельного времени решаются следующие задачи.
1) отображается переход моделируемой системы из одного состояния в другое;
2) производится синхронизация работы компонент модели;
3) изменяется масштаб времени «жизни» (функционирования) исследуемой
системы;
4) производится управление ходом модельного эксперимента.
5) моделируется квазипараллельная реализация событий в модели;
Приставка «квази» в данном случае отражает последовательный характер об-
работки событий (процессов) в ИМ, которые в реальной системе возникают (про-
текают) одновременно.
Необходимость решения последней задачи связана с тем, что в распоряжении
исследователя находится, как правило, однопроцессорная вычислительная систе-
ма, а модель может содержать значительно большее число одновременно работаю-
щих подсистем, Поэтому действительно параллельная (одновременная) реализа-
ция всех компонент модели невозможна. Даже если используется так называемая распределенная модель, реализуемая на нескольких узлах вычислительной сети,
совсем необязательно число узлов будет совпадать с числом одновременно рабо-
тающих компонент модели. Немного забегая вперед, следует отметить, что реали-
зация квазипараллельной работы компонент модели является достаточно сложной
технической задачей.
|
|
Способы управления модельным временем
Ранее были названы два метода реализации механизма модельного времени — с
постоянным шагом и по особым состояниям.
Выбор метода реализации механизма модельного времени зависит от назначе-
ния модели, ее сложности, характера исследуемых процессов, требуемой точности
результатов и т. д.
При использовании метода постоянного шага отсчет системного времени ве-
дется через фиксированные, выбранные исследователем интервалы времени. Со-
бытия в модели считаются наступившими в момент окончания этого интервала.
Погрешность в измерении временных характеристик системы в этом случае зави-
сит от величины шага моделирования dt.
Метод постоянного шага предпочтительнее, если
~ события появляются регулярно, их распределение во времени достаточно равномерно;
~ число событий велико и моменты их появления близки;
~ невозможно заранее определить моменты появления событий.
Данный метод управления модельным временем достаточно просто реализовать
в том случае, когда условия появления событий всех типов в модели можно пред-
ставить как функцию времени.
Пусть, например, событие состоит в том, что летящий самолет пересекает неко-
торый воздушный рубеж, расстояние до которого равно R. Если самолет движется
по прямой с постоянной скоростью V, то можно вычислять путь, пройденный само
летом, с интервалом времени dt: S:= S+ Vdt. Соответственно событие считается
наступившим, если выполняется условие S > R, а момент времени наступления со-
бытия принимается равным n. d t, где n — номер шага моделирования, на котором
условие стало истинным.
|
|
В общем виде алгоритм моделирования с постоянным шагом представлен На
рис. 1. (tм — текущее значение модельного времени, Тм — интервал моделирования)-
ва.
С целью некоторого ~оживления~ приведенной выше схемы вернемся к примеру с самолетом. Введем в рассматриваемую ситуацию еще одно событие, которое
состоит в том, чтодиспетчер, наблюдающий за самолетом, вводит данные о нем в
некую систему управления. Процесс ввода заключается в наборе на клавиатуре
определенной текстовой информации. Известна длина текста (в символах) и средняя скорость ввода одного символа. В ходе модельного эксперимента требуется определить,
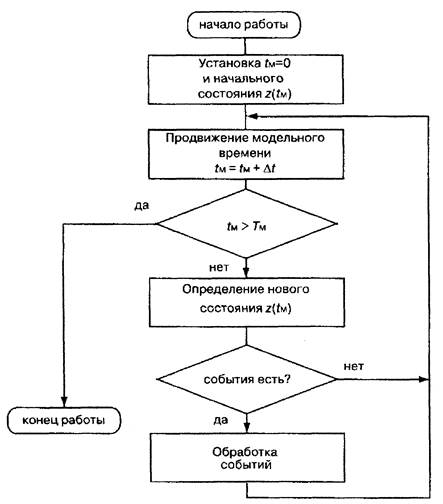
Рис. 1. Алгоритм моделирования с постоянным шагом
закончит ли диспетчер ввод текста до пересечения самолетом заданного
рубежа. Алгоритм управления модельным временем для рассматриваемого приме-
ра показан на рис. 2.
Очевидно, что оба рассматриваемых процесса (полет самолета и ввод информа-
ции) должны быть «привязаны» к единой оси модельного времени. Вместес тем
каждый из них характеризуется различной скоростью, разной степенью дискрет-
ностии т. д. В такой ситуации для различных значений шага моделирования ∆ t
экспериментможет дать разные результаты. Причем если шаг будет слишком боль-
шим, то результат, скорее всего, будет неверным. Момент окончания ввода информации будет всегда совпадать с моментом пересечения самолетом заданного рубежа. Такая ситуация показана на рис. 3.
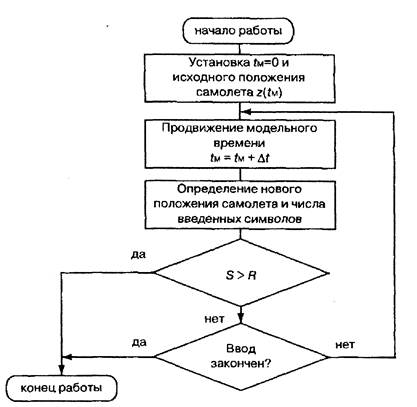
Рис. 2. Пример моделирования с постоянным шагом
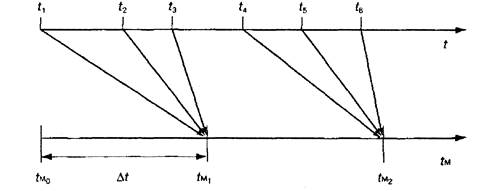
Рис.3. Пример привязки событий к оси модельного времени
Приведенный пример показывает, что выбор величины шага моделирования является нелегким и
очень важным делом. Универсальной методики решения этой проблемы не су-
ществует, но во многих случаях можно использовать один из следующих под-
ходов:
~ принимать величину шага равной средней интенсивности возникновения со-
бытий различных типов;
~ выбирать величину d t равной среднему интервалу между наиболее частыми
(или наиболее важными) событиями.
При моделировании поособым состояниям системное время каждый раз из-
меняется на величину, строго соответствующую интервалу времени до момента наступления очередного события. В этом случае события обрабатываются в поряд-
ке их наступления, а одновременно наступившими считаются только те, которые
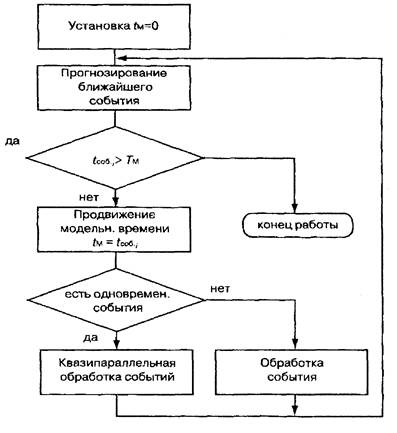
Рис. 4. Алгоритм моделирования по особым состояниям
являются одновременными в действительности.
Метод моделирования по особым состояниям сложнее в реализации, так как
для него требуется разработка специальной процедуры планирования событий (так
называемого календаря событий).
Моделирование по особым состояниям целесообразно использовать, если:
~ события распределяются во времени неравномерно или интервалы между
ними велики;
• предъявляются повышенные требования к точности определения взаимного
положения событий во времени;
- необходимо реализовать квазипараллельную обработку одновременных событий.
Дополнительное достоинство метода заключается в том, что он позволяет эко-
номить машинное время, особенно при моделировании систем периодического дей-
ствия, в которых события длительное время могут не наступать.
Обобщенная схема алгоритма моделирования ло особым состояниям представ-
лена на рис.4 (t соб. — прогнозируемый момент наступления i-го события.
Чтобы ~почувствовать разницу~ в использовании двух методов
управления модельнымвременем, вернемся еще раз к примеру с летящим самоле-
том и сидящим диспетчером,
На этот раз перед разработчиком модели встает иная проблема: что пони-
мать под "особыми состояниями", которые должны влиять на изменение мо-
дельного времени? На практике обычно вместо состояний рассматривают со-
бытия, определяющие смену состояний моделируемого процесса. Для процесса
ввода информации диспетчером такой переход выполняется достаточно просто:
событие — это ввод очередного символа; другими словами, ввод очередного сим-
вола «продвигает» модельное время на соответствующий интервал. Все так про-
сто потому что процесс ввода является дискретным. А что делать с непрерывно
летящим самолетом? Здесь возможны два варианта: либо увязать расчет нового
положения самолета с моментом ввода очередного символа, либо изменить в
модели представление полета с непрерывного на дискретное (например, рас-
сматривать перемещение не самого самолета в воздухе, а его «образах на экране
индикатора).
Алгоритм работы модели для первого варианта приведен на рис. 5.
А какбыть в том случае, когда и полет самолета, и работа диспетчера подверже-
ны влиянию случайных факторов? Ответим на этот вопрос для не очень слож-
ного, но весьма распространенного в практике моделирования варианта, когда рас-
сматриваемые процессы могут быть описаны с помощью случайных величин,
распределенных по заданному закону.
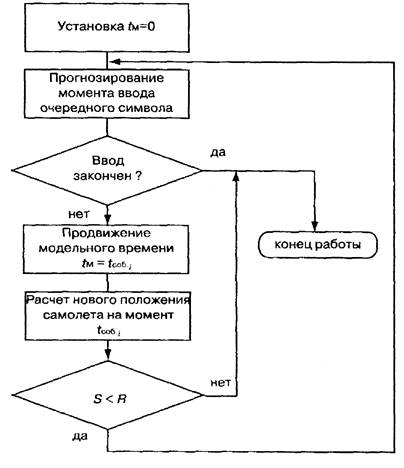
Рис. 5. Пример работы модели по особым состояниям
Для самолета такой величиной будет служить скорость полета, а для диспетче-
ра — скорость ввода символов. В этом случае изменение модельного времени и рас-
чет нового положения самолета также можно увязатьсвводом очередного символа. Логика работы такой модели по-прежнему будет соответствовать алгоритму,
изображенному на рис.5. Отличие заключается лишь в том, что прогноз времени
ввода очередного символа выполняется на основе функции распределения соот-
ветствующей случайной величины. Так, если скорость ввода символов подчиняет-
ся нормальному закону с параметрами т и d, то очередное i-е значение модельного
времени t мi, определяется следующим образом:
tм,. = tмi-1,. + norm(m, d).
В этом выражении слагаемое norm(m, d) означает обращение к генератору слу-
чайных чисел, распределенных по нормальному закону.