МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ.
МАТРИЦЫ
Определение 3.1. Матрицей называется прямоугольная таблица, состоящая из элементов  и содержащая
и содержащая  строк и
строк и  столбцов.
столбцов.  . Таблицу заключают в круглые или квадратные скобки, либо ограничивают двойными чертами.
. Таблицу заключают в круглые или квадратные скобки, либо ограничивают двойными чертами.  .
.
Определение 3.2. Число  называют размером матрицы. Матрица называется:
называют размером матрицы. Матрица называется:
1) прямоугольной, если  ;
;
2) квадратной, если  .
.
Определение 3.3. Число  называют порядком квадратной матрицы.
называют порядком квадратной матрицы.
Определение 3.4. Матрицу, имеющую одну строку, называются строкой, а число элементов в строке – длиной строки.
Определение 3.5. Матрицу, имеющую один столбец, называют столбцом.
Определение 3.6. Матрица, все элементы которой равны нулю, называется нулевой матрицей.
Определение 3.7. Элементы  квадратной матрицы составляют главную диагональ матрицы. Элементы
квадратной матрицы составляют главную диагональ матрицы. Элементы  составляют побочную диагональ квадратной матрицы.
составляют побочную диагональ квадратной матрицы.
Определение 3.8. Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, т. е. матрица вида:
 − называется диагональной.
− называется диагональной.
Определение 3.9. Диагональная матрица, у которой  , называется единичной, и обозначается
, называется единичной, и обозначается  или
или  , т. е.
, т. е. 
Определение 3.10. Квадратная матрица, у которой все элементы, стоящие под (над) главной диагональю, равны нулю, называют верхней (нижней) треугольной матрицей.
Операции над матрицами и их свойства
Равенство матриц
Две матрицы равны, если равны:
1) размеры матриц;
2) элементы матриц, стоящие на одинаковых местах.
Сложение матриц
Складывать можно только матрицы одинаковых размеров.
Определение 3.11. Суммой матриц  и
и  называется матрица
называется матрица  , элементы которой равны суммам соответствующих элементов данных матриц.
, элементы которой равны суммам соответствующих элементов данных матриц.
 ,
,  , (
, ( ;
;  ).
).
Свойства операции сложения:
1)  ;
;
2)  .
.
Умножение матрицы на число
Определение 3.12. Произведением матрицы  на число
на число  называется матрица
называется матрица  , элементы которой получаются из соответствующих элементов матрицы
, элементы которой получаются из соответствующих элементов матрицы  умноженных на число
умноженных на число  .
.
 ,
,  .
.
Свойства операции:
1)  ;
;
2) 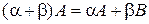 ;
;
3)  .
.
4) Разность  матриц одинаковых размеров определяется равенством
матриц одинаковых размеров определяется равенством  .
.
Умножение матриц
Определение 3.13. Произведением двух матриц  и
и  , причём число столбцов матрицы
, причём число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  , называется матрица
, называется матрица  , у которой элемент
, у которой элемент
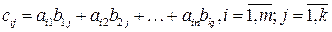 .
.
В общем случае  .
.
Пример 3.1. Найти  и
и  , если
, если 
 .
.
Решение. 
 . Тогда
. Тогда  . В обратном порядке
. В обратном порядке  перемножить нельзя, т. к. число строк
перемножить нельзя, т. к. число строк  не равно числу столбцов
не равно числу столбцов  .
.
Свойства операции:
1)  ;
;
2)  ;
;
3)  .
.
Определение 3.14. Матрицы, для которых выполняется равенство  , называются перестановочными (коммутирующими).
, называются перестановочными (коммутирующими).
Транспонирование матриц
Определение 3.15. Замена строк столбцами в матрице называется транспонированием.
Определение 3.16. Матрица  получающаяся из
получающаяся из  заменой строк столбцами, называется транспонированной по отношению к
заменой строк столбцами, называется транспонированной по отношению к  .
.
Операция транспонирования обозначается символом  или
или  .
.
Свойства операции:
1)  ;
;
2)  ;
;
3)  .
.
Квадратная матрица  называется
называется
1) симметрической, если  ;
;
2) кососимметрической, если  ;
;
3) ортогональной, если  .
.
Пример 3.2. Является ли матрица  симметрической?
симметрической?
Решение. Найдём  , т. к.
, т. к.  , то матрица
, то матрица  симметрическая.
симметрическая.
Обращение матриц
Определение 3.17. Квадратная матрица  называется обратимой, если существует квадратная матрица
называется обратимой, если существует квадратная матрица  , удовлетворяющая условиям
, удовлетворяющая условиям  .
.
Матрица  называется обратной к
называется обратной к  и обозначается
и обозначается  .
.
Свойства операции:
1)  ;
;
2)  .
.
Пример 3.3. Найти матрицу обратную к матрице  .
.
Решение. По определению  ,
, 
 , тогда
, тогда  Отсюда
Отсюда  .
.
Проверка. По определению  .
.  и
и  .
.
3.1. Вычислить:
1)  , 2)
, 2)  .
.
3.2. Вычислить:
1)  , 2)
, 2)  ,
,
3)  , 4)
, 4)  .
.
3.3. Матрица А имеет размер  , матрица С – размера
, матрица С – размера  . Существует ли произведение
. Существует ли произведение  ? Каковы размеры матриц B и ABC?
? Каковы размеры матриц B и ABC?
3.4. Проверить существует ли произведение матриц, если да, то вычислить его.
1)  , 2)
, 2)  ,
,
3)  , 4)
, 4)  .
.
3.5. Протранспонировать матрицу:
1)  2)
2)  3)
3)  4)
4) 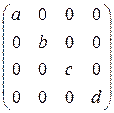
3.6. Всегда ли верно матричное тождество  . Привести примеры перестановочных матриц.−
. Привести примеры перестановочных матриц.−
3.7. Вычислить  , если
, если
1)  ,
, 
2)  ,
, 
3.8. Вычислить  .
.
1)  , 2)
, 2)  ,
,
3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  .
.
3.9. Найти все матрицы, перестановочные с матрицей
1)  , 2)
, 2)  .
.
3.10. Найти обратные матрицы для
1)  , 2)
, 2)  .
.
3.11. «Следом» квадратной матрицы называется сумма элементов главной диагонали. Доказать, что след  равен следу
равен следу  .
.
ОПРЕДЕЛИТЕЛИ.
Определение 3.18. Каждой квадратной матрице  -го порядка по некоторому закону может быть поставлено в соответствие число
-го порядка по некоторому закону может быть поставлено в соответствие число  , называемое определителем матрицы
, называемое определителем матрицы  , или просто определителем
, или просто определителем  -го порядка.
-го порядка.
Определение 3.19. Определителем второго порядка называют выражение:  .
.
Из произведения элементов главной диагонали отнимается произведение элементов побочной диагонали.
Пример 3.4. Вычислить  .
.
Решение.  .
.
Определение 3.20. Определителем третьего порядка называют выражение:

Определение 3.21. Минором  элемента
элемента  определителя
определителя 
 -го порядка называется определитель
-го порядка называется определитель  -го порядка, получающийся из
-го порядка, получающийся из  вычёркиванием
вычёркиванием  −строки и
−строки и  −столбца.
−столбца.
Определение 3.22. Алгебраическим дополнением  элемента
элемента  называется его минор, взятый со знаком
называется его минор, взятый со знаком  , т. е.
, т. е.  .
.
Определение 3.23. Определителем  -го порядка называется сумма произведений элементов любой строки (столбца) на их алгебраические дополнения:
-го порядка называется сумма произведений элементов любой строки (столбца) на их алгебраические дополнения:  и т. д.
и т. д.
Так как определители 2 и 3-го порядка уже определены, то находим определители высших порядков через них.
Пример 3.5. Найти  .
.
Решение.

 .
.
Пример 3.6. Найти  .
.
Решение:

Определитель нижнетреугольной (верхнетреугольной) матрицы равен произведению элементов главной диагонали.
Нахождение определителей ( ) по определению громоздкая процедура, её можно упростить, если узнать свойства определителей.
) по определению громоздкая процедура, её можно упростить, если узнать свойства определителей.
Свойства определителей.
Свойство 1. Определитель не меняется при транспонировании (равноправие строк и столбцов определителя).
Т. к. строки и столбцы равноправны, сформулируем свойства только для строк, для столбцов они будут тоже выполняться.
Свойство 2. Определитель равен нулю, если одна строка состоит из нулей. (Доказать самостоятельно.)
Свойство 3. При перестановке двух строк определитель меняет знак. (Доказать самостоятельно.)
Свойство 4. Определитель, имеющий одинаковые строки, равен нулю.
Свойство 5. Если элементы некоторой строки умножить на число  , то определитель увеличиться в
, то определитель увеличиться в  раз, и наоборот, из строки можно вынести общий множитель за знак определителя.
раз, и наоборот, из строки можно вынести общий множитель за знак определителя.
Свойство 6. Определитель, содержащий две пропорциональные строки, равен нулю.
Свойство 7. Если элементы некоторой строки определителя  представлены в виде суммы двух слагаемых, то и сам определитель равен сумме двух определителей
представлены в виде суммы двух слагаемых, то и сам определитель равен сумме двух определителей  и
и  . В определителе
. В определителе  указанная строка состоит из первых слагаемых, в
указанная строка состоит из первых слагаемых, в  –из вторых. Остальные элементы в
–из вторых. Остальные элементы в  и
и  те же, что и в
те же, что и в  .
.
Свойство 8. Определитель не меняется, если к элементам одной строки прибавить элементы другой строки, умноженные на одно число.
Свойство 9. Сумма произведений элементов любой строки на алгебраические дополнения к соответствующим элементам другой строки равна нулю.
Свойство 10. Определитель произведения двух матриц равен произведению определителей этих матриц, т. е.  (без доказательства).
(без доказательства).
Если в определителе  -го порядка одна из строк имеет один элемент, отличный от нуля, то по определению, данный определитель равен произведению этого элемента на его алгебраическое дополнение (т. е. определитель
-го порядка одна из строк имеет один элемент, отличный от нуля, то по определению, данный определитель равен произведению этого элемента на его алгебраическое дополнение (т. е. определитель  -го порядка).
-го порядка).
3.4. Алгоритм вычисления определителя  -го порядка
-го порядка
1) Получаем в какой-либо строке (столбце), используя свойство 8, нули, кроме одного элемента.
2) Раскрываем определитель по этой строке (столбцу) и приходим к вычислению определителя  порядка.
порядка.
Дальше повторяем пункт 1 и 2, столько раз, пока не придём к определителю 3 порядка, который умеем вычислять.
Пример 3.7. Вычислить  .
.
Решение. Получаем нули в первом столбце (можно во 2 строке, 4 столбце или 4 строке), т. к. один нуль там уже есть.
Удобно, когда в этой строке есть единица. Умножим первую строку на  и сложим с 3 строкой (по свойству 8), третью строку сложим с 4 стро
и сложим с 3 строкой (по свойству 8), третью строку сложим с 4 стро  кой, определитель не изменится.
кой, определитель не изменится.





3.12. Вычислить определители
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
3.13. Доказать, что для равенства нулю определителя второго порядка, необходимо и достаточно, чтобы его строки были пропорциональны. (коэффициент пропорциональности может быть равен 0).
3.14. Вычислить:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
7)  8)
8)  .
.
3.15. Доказать, что определитель диагональной матрицы равен произведению диагональных элементов.
3.16. Используя свойства определителя, доказать тождества:
1) 
2) 
3) Числа 19, 38 делятся на 19. Не вычисляя определителя, докажите, что определитель  делится на 19.
делится на 19.
3.17. Вычислить:
1)  2)
2)  3)
3) 
4) 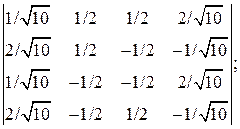 5)
5)  6)
6) 
7)  8)
8)  .
.
Вычислить 1) и 2) методом Гаусса.
ОБРАТНАЯ МАТРИЦА. РАНГ МАТРИЦЫ. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ.
ОБРАТНАЯ МАТРИЦА
Определение 4.1. Квадратная матрица называется вырожденной (особенной), если её определитель равен нулю.
Определение 4.2. Квадратная матрица называется невырожденной (неособенной), если её определитель отличен от нуля.
Определение 4.3. Матрица  называется обратной для матрицы
называется обратной для матрицы  , если
, если  .
.
Выясним, когда существует обратная матрица.
1 случай.  – вырожденная матрица, т. е.
– вырожденная матрица, т. е.  , тогда обратной матрицы не существует.
, тогда обратной матрицы не существует.
2 случай.  – невырожденная матрица, т. е.
– невырожденная матрица, т. е.  .
.
Пусть  .
.  . Обозначим
. Обозначим  − присоединённую матрицу, где
− присоединённую матрицу, где  алгебраические дополнения элементов
алгебраические дополнения элементов  .
.
Тогда  .
.
Значит, для невырожденной матрицы обратная матрица существует и равна  .
.
Пример 4.1. Найти  для
для  .
.
Решение. 1) Найдём  . Значит
. Значит  – невырожденная матрица и
– невырожденная матрица и  существует.
существует.
2) Найдём  – присоединённую матрицу, для этого вычислим алгебраические дополнения элементов матрицы
– присоединённую матрицу, для этого вычислим алгебраические дополнения элементов матрицы  .
.
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  ; тогда
; тогда  .
.
Протранспонируем  , т. е.
, т. е.  .
.
Тогда  .
.
4.1. Доказать, что  .
.
4.2. Найти обратные матрицы и сделать проверку  :
:
1.  ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  .
.
РАНГ МАТРИЦЫ
Рассмотрим прямоугольную матрицу  .
.
Пусть  . Выделим в этой матрице
. Выделим в этой матрице  строк и
строк и  столбцов.
столбцов.
Определение 4.4. Минором  -го порядка матрицы
-го порядка матрицы  называется определитель
называется определитель  - го порядка, составленный из элементов, стоящих на пересечении
- го порядка, составленный из элементов, стоящих на пересечении  строк и
строк и  столбцов.
столбцов.
В матрице  можно составить
можно составить 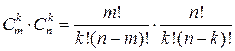 миноров
миноров  - го порядка.
- го порядка.
Пример 4.2. Найти все миноры матрицы  .
.
Решение. Т. к.,  то:
то:
1. миноров 1 порядка  (Это элементы матрицы)
(Это элементы матрицы)
2. миноров 2 порядка  . Это, например,
. Это, например,  ,
,  ,
,  и др.
и др.
3. миноров 3 порядка  . Это
. Это  ,
,  ,
,  ,
, 
Если посчитать миноры, то окажется, что:
1) есть отличные от нуля миноры 1 порядка;
2) есть отличные от нуля миноры 2 порядка;
3) миноры 3 порядка все равны 0;
В этом случае будем говорить, что ранг матрицы A равен 2.
Определение 4.5. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.
Таким образом, если ранг матрицы равен  , то среди миноров матрицы есть по крайней мере один минор
, то среди миноров матрицы есть по крайней мере один минор  -го порядка отличный от нуля, в то время как все миноры
-го порядка отличный от нуля, в то время как все миноры  - го порядка и выше равны нулю. Ранг только нулевой матрицы равен нулю.
- го порядка и выше равны нулю. Ранг только нулевой матрицы равен нулю.
Ранг матрицы будем обозначать  .
.
Для вычисления ранга матрицы существует метод (метод Гаусса), не требующий вычисления определителей, основанный на элементарных преобразованиях.
Определение. 4.6. Элементарными преобразованиями матрицы называются следующие преобразования:
1) транспонирование матрицы;
2) перестановка строк или столбцов;
3) умножение всех элементов строки (столбца) на любое число, отличное от нуля;
4) прибавление к элементам строки(столбца) соответствующих элементов строки (столбца), умноженных на одно и то же число.
Теорема 4.1. (О б элементарных преобразованиях).
При элементарных преобразованиях матрицы ее ранг не меняется.