Исследование формы эллипса по его уравнению.

ТЕМА II. «ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»

 

ОПОРНЫЙ КОНСПЕКТ ПО ТЕМЕ:

«Эллипс»

Каноническое уравнение эллипса.

Определение 1. Э лл ипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, бóльшая, чем расстояние между фокусами.

 

 

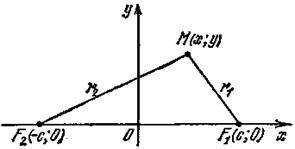
Рис. 1

 

Составим уравнение эллипса с фокусами в данных точках F₁ и F₂. Для этого выберем прямоугольную систему координат так, чтобы ось Ох проходила через фокусы, а начало координат делило отрезок F₁F₂ пополам (рис.1).

Обозначив F₁F₂=2c, получим F₁ (c; 0) и F₂ (–с; 0). Пусть М (х; у) – произвольная точка эллипса.

Определение 2. Расстояния r₁=F₁M и r₂=F₂M называются фокальными радиусами точки М.

Положим

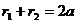; (1)

тогда согласно определению эллипса 2а – величина постоянная, причем 2а>2с, т.е. а>с.

По формуле расстояния между двумя точками находим

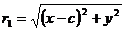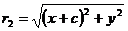и . (2)

Подставив найденные значения r₁ и r₂ в равенство (1), получим уравнение эллипса

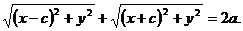(3)

Преобразуем уравнение (3) следующим образом:

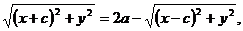
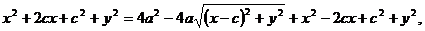
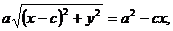
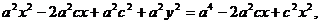
т. е.

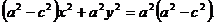
Так как а > с, то а²–с²>0. Положим

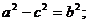(4)

 

тогда последнее уравнение примет вид

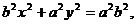
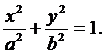
или

(5)

 

 

Так как координаты х и у любой точки М эллипса удовлетворяют уравнению (3), то они удовлетворяют и уравнению (5).

Покажем, что справедливо и обратное: если координаты точки М(х; у) удовлетворяют уравнению (5), то она принадлежит эллипсу.

Пусть М (х; у) – произвольная точка, координаты которой удовлетворяют уравнению (5). Так как из (5) следует

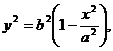(6)

то 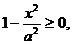откуда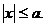

Подставив (6) в соотношения (2) и проведя необходимые упрощения, получим

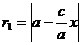и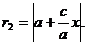

Но так как а > с > 0 и 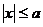, то

и ,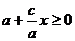

откуда

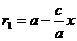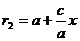и (7)

и, следовательно, 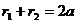, т. е., точка М (х; у) действительно принадлежит эллипсу.

Определение 3. Уравнение (5) называется каноническим уравнением эллипса.

Исследование формы эллипса по его уравнению.

Определим форму эллипса по его каноническому урав­нению (5).

1) Координаты точки О (0; 0) не удовлетворяют уравнению (5), поэтому эллипс, определяемый этим уравнением, не проходит через начало координат.

2) Найдем точки пересечения эллипса с осями координат. Положив в уравнении (5) у=0, найдем х = ± а. Следовательно, эллипс пересекает ось Ох в точках A₁ (a; 0) и А₂ (–а; 0). Положив в уравнении (5) х = 0, найдем точки пересечения эллипса с осью Оу: В₁ (0; b) и В₂ (0; –b) (рис. 2).

3) Так как в уравнение (5) переменные х и у входят только в четных степенях, то эллипс симметричен относительно координатных осей, а следовательно, и относительно начала координат.

4) Определим область изменения переменных х и у.

Выше мы уже показали, что

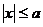, т.е. .

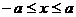Переписав уравнение эллипса (5) в виде

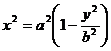, получим 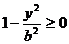, откуда

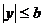, или .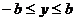

Таким образом, все точки эллипса находятся внутри прямоугольника, ограниченного прямыми х = а, х = – а, у = b и у = – b (см. рис. 2).

Рис. 2

 

5) Переписав (5) соответственно в виде

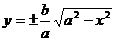и ,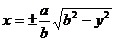

мы видим, что при возрастании | х |от 0 до а величина | у |убывает от b до 0, а при возрастании | у | от 0 до b величина | х| убывает от а до 0. Эллипс имеет форму, изображенную на рис. 3.

Определение 4. Точки А₁, А₂, B₁, B₂ пересечения эллипса с осями координат назы­ваются вершинами эллипса. Из равенства (4) следует, что а > b.

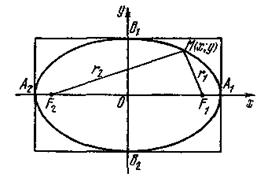
Рис. 3

Определение 5. Отрезок А₁А₂ (А₁А_г=2а, 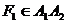, 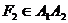) называется большой осью эллипса, а отрезок В₁В₂ (В₁B₂=2b) – малой осью. Оси A₁A₂ и В₁В₂ являются осями симметрии эллипса, а точка О – центром симметрии (или просто центром) эллипса.

3. Другие сведения об эллипсе. Вп. 2 мы установили, что в каноническом уравнении эллипса а > b. Если же а < b, то уравнение (5) не является каноническим уравнением эллипса. Однако и в этом случае уравнение (5) определяет эллипс, большая ось которого 2b лежит на оси Оу, а малая ось 2а – на оси Ох. Фокусы такого эллипса находятся в точках F₁ (0; с) и F₂ (0; – с), где 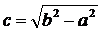(рис. 4).

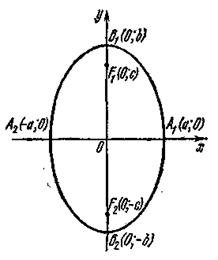
Рис. 4

 

Определение 6. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси и обозначается буквой ε.

Если a > b,то по определению

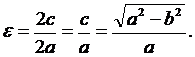(8)

При а < b имеем

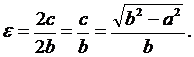(9)

Из формул (8) и (9) следует 0 ≤ ε ≤ 1. При этом с увеличением разности между полуосями а и b увеличивается соответствующим образом и эксцентриситет эллипса, приближаясь к единице; при уменьшении разности между а и b уменьшается и эксцентриситет, приближаясь к нулю.

Таким образом, по величине эксцентриситета можно судить о форме эллипса: чем больше эксцентриситет, тем более эллипс вытянут вдоль большой оси; чем меньше эксцентриситет, тем более эллипс по форме ближе к окружности. В частности, если b = a, то ε = 0, и уравнение эллипса

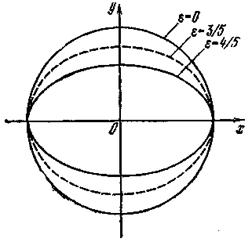
Рис. 5

примет вид х² + у² = а², которое определяет окружность радиуса а с центром в начале координат. Таким образом, окружность можно рассматривать как частный случай эллипса, у которого полуоси равны между собой, а, следовательно, эксцентриситет равен нулю.

Из рис. 5, на котором изображены эллипсы 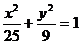(ε = 4/5), 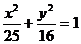(ε = 3/5) и окружность х² + у² = 25 (ε = 0), хорошо видна зависимость формы эллипса от его эксцентриситета.

Определение 7. Прямые, параллельные малой оси эллипса, находящиеся на расстоянии 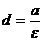от нее, называются директрисами эллипса.

Тогда уравнения директрис эллипса имеют вид:

, .

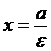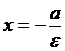В заключение поясним, как можно построить эллипс

.

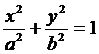Для этого на осях координат строим вершины эллипса А₁ (а; 0), А₂ (–а; 0), В₁ (0; b) и В₂ (0; – b). Затем из вершины B_t (можно из В₂) радиусом, равным а, на большой оси делаем засечки F₁ и F₂ (рис. 6). Это будут фокусы эллипса, потому что а² – b² = с². Далее, берем нерастяжимую нить, длина которой равна 2а, и закрепляем ее концы в найденных фокусах. Натягиваем нить острием карандаша и описываем кривую, оставляя нить все время в натянутом состоянии.

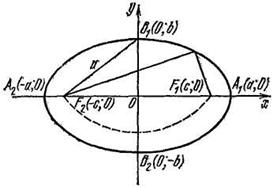
Рис. 6

 

В ряде задач математики и механики приходится иметь дело с эллипсом, центр которого находится не в начале координат, а в точке О' (х₀; у₀). Если оси эллипса параллельны осям координат, то уравнение эллипса имеет вид

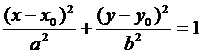. (10)

Это уравнение эллипса со смещенным центром.