Лекция 11. Основные теоремы дифференционного исчисления
План
Определение экстремума функции
Теорема Ферма и ее геометрический смысл
Теорема Ролля
Теорема Лагранжа. Формула Лагранжа
Теорема Коши
Теорема Дарбу
Производные высших порядков
Определение экстремума функции
Определение 1. Пусть функция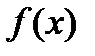 
определена на 
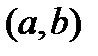. Говорят, что 
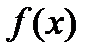имеет локальный максимум (минимум) в точке 
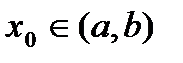, если существует такая окрестность точки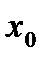 
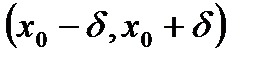, что для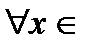 
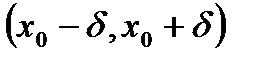выполняется неравенство:
.
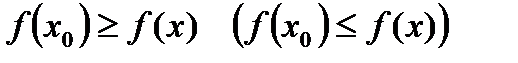Локальный максимум (минимум) называется строгим, если окрестность 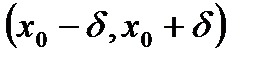можно выбрать так, что для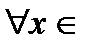 
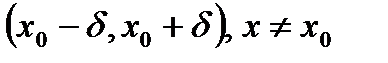, выполняется неравенство:
.
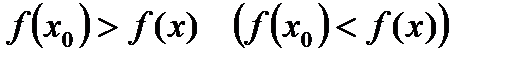Определение 2. Точки локального минимума и локального максимума называются точками локального экстремума.
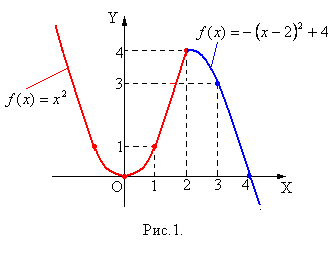
Пример. Рассматривается функция (рис.1):
.
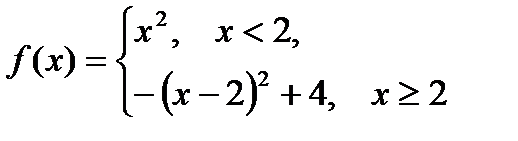По определению 2 точки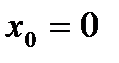 
и 
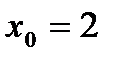являются точками локального минимума и локального максимума соответственно.
Теорема Ферма и ее геометрический смысл
Теорема (Ферма). Пусть функция 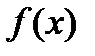определена на 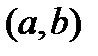и имеет локальный экстремум в точке 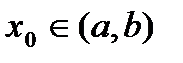. Если 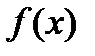дифференцируема в точке 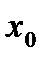, то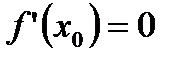 
.
Доказательство. Для определенности будем считать, что в точке 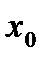локальный максимум. Рассмотрим разностное отношение
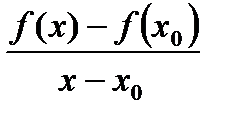. (10)
Поскольку 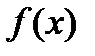дифференцируема в точке 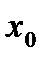, то существует
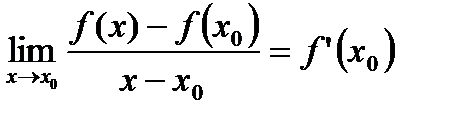. (15)
Для существования предела (15) надо, чтобы
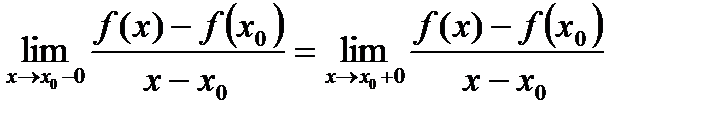, (20)
но, учитывая, что в точке локальный максимум, имеем
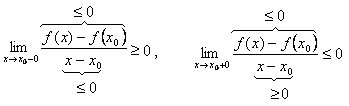
Тогда равенство (20) возможно лишь, когда:
,
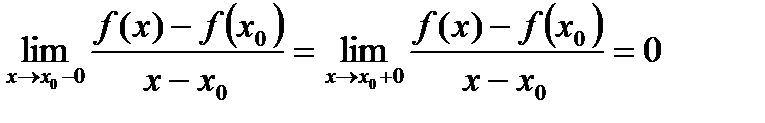т.е. .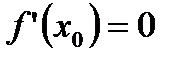
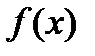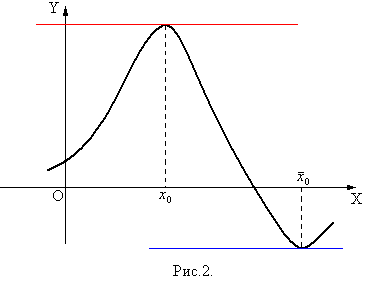
Дифференцируемость функции в точке 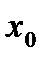геометрически говорит о существовании касательной к графику функции в точке 
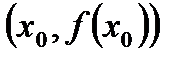, а значение 
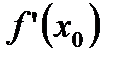- это тангенс угла наклона касательной к положительному направлению оси ОХ. Таким образом 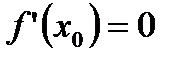геометрически означает, что касательная к графику в точке 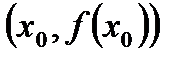существует, и эта касательная параллельна оси ОХ, а геометрический смысл теоремы Ферма состоит в следующем: в точке локального эстремума касательная к графику функции, если она вообще существует, будет параллельна оси ОХ (рис.2).
Теорема Ролля
Определение. Пусть функция 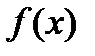определена на 
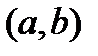. Если в каждой точке интервала 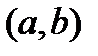функция 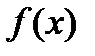имеет производную, то будем говорить, что 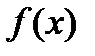дифференцируема в .
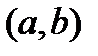Теорема (Ролля). Пусть функция 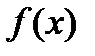определена на 
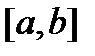и выполняются условия:
1. 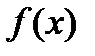непрерывна на 
;
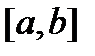2. 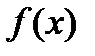дифференцируема в ;
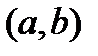3. 
,
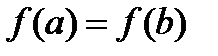Тогда существует точка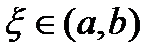 
, что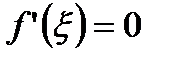 
.
Доказательство. По второй теореме Вейерштрасса поскольку 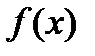непрерывна на 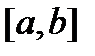, она достигает на 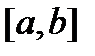своих инфимума и супремума. Пусть
, 
.
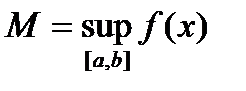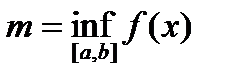Рассмотрим два возможных варианта:
1. 
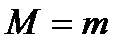. Если инфимум и супремум функции совпадают, то 
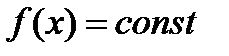, а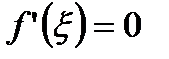 
в любой точке .
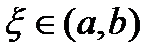2. 
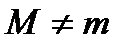. Поскольку 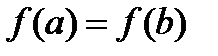, то наибольшего или наименьшего своего значения функция обязательно достигает в 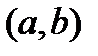. Допустим, что в 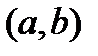функция достигает супремума. Пусть это происходит в точке : 
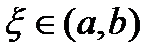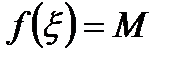. В точке 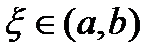функция имеет локальный максимум, по второму условию теоремы 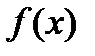дифференцируема в точке 
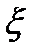, поэтому по теореме Ферма: 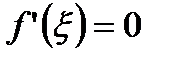, что и нужно было доказать.
Замечание 1. Если предположить, что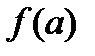 
и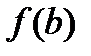 
не просто равные, а 
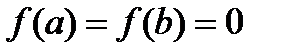, то теорему Ролля можно сформулировать иначе: между любыми двумя нулями дифференцируемой функции находится хотя бы один нуль производной.
Замечание 2. Все условия теоремы Ролля являются важными для ее выполнения.
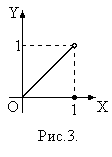Проверим истинность замечания 2.
1. Рассмотрим функцию (рис.3):
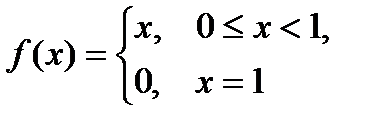
которая определена на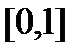 
.Эта функция удовлетворяет всем условиям теоремы Ролля, кроме условия 1: 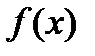не является непрерывной на 
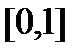, она имеет разрыв в точке 
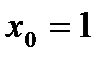. Это «нарушение» приводит к невыполнению теоремы: в 
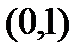не существует точки, в которой производная равнялась бы нулю.
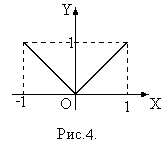
2. Рассмотрим функцию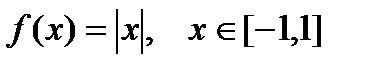 
(рис.4). Эта функция не удовлетворяет условию 2 предыдущей теоремы, потому что в точке 
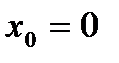является недифференцируемой. Теорема не выполняется: на 
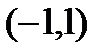нет точки, где производная функции будет равняться 0.
3. Для функции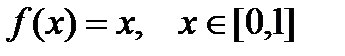 
не выполняется условие 3, теорема не выполняется.
Пример. Показать, что уравнение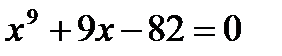 
имеет не больше, чем один действительный корень. Обозначим: 
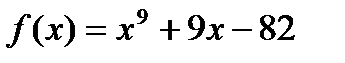, тогда 
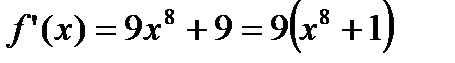. Понятно, что 
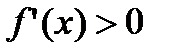для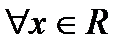 
. Если б уравнение 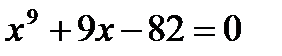имело хотя бы 2 действительных корня, то есть функция 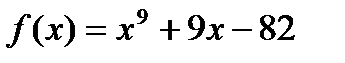имела хотя бы 2 нуля, то по теореме Ролля между ними был бы хотя бы один нуль производной, но производная не имеет нулей. Таким образом, уравнение 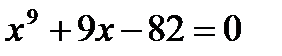имеет лишь один действительный корень.
Теорема Лагранжа. Формула Лагранжа
Теорема (Лагранжа). Пусть функция 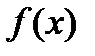определена на 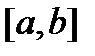и выполняются условия:
1. 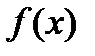непрерывна на ;
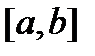2. 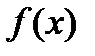дифференцируема в .
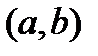Тогда существует точка 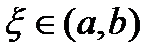, что
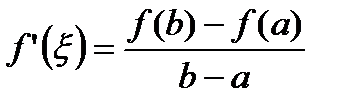. (30)
Доказательство. Построим вспомогательную функцию
.
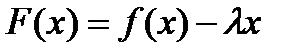Коэффициент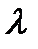 
выберем так, чтобы выполнялось условие: 
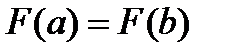. По определению функции 
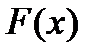это эквивалентно:
,
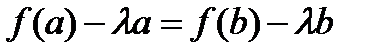откуда
,
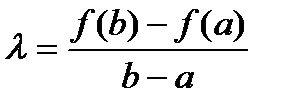а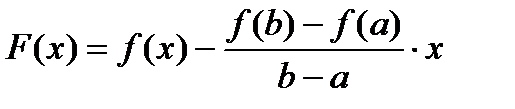 
.
Для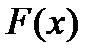 
выполнены все условия теоремы Ролля, поэтому существует 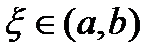, что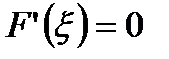 
:
,
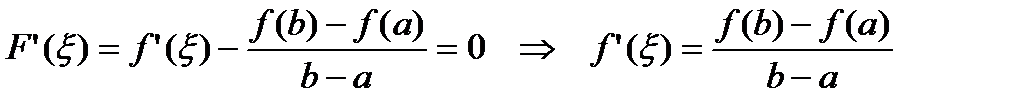что и нужно было доказать.
Формулу (30) можно записать в эквивалентном виде:
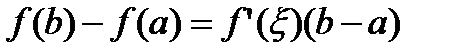. (40)
Формула (40) называется формулой Лагранжа.
Замечание. Теорема Ролля является частным случаем теоремы Лагранжа. Действительно, если к условиям 1,2 теоремы Лагранжа добавить условие 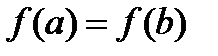, то формула (30) будет иметь вид: 
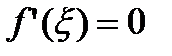, что отвечает теореме Ролля.
Геометрический смысл теоремы Лагранжа понятен из рис.5: если выполняются условия теоремы, то найдется такая точка 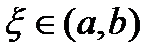, что касательная к графику функция, проведенная в точке 
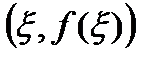, будет параллельна секущей к графику, проведенной через точки 
, 
.
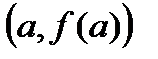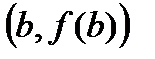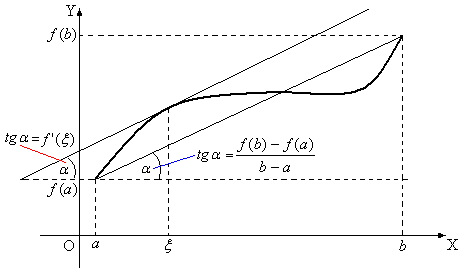
Рис.5.
Теорема Коши
Теорема (Коши). Пусть функции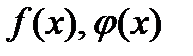 
рассматриваются на 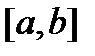и выполняются условия:
1. 
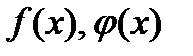непрерывны на ;
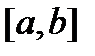2. 
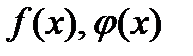дифференцируемы в ;
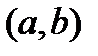3. 
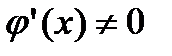для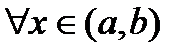 
.
Тогда существует точка 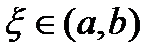, что
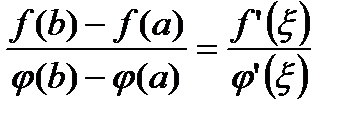. (50)
Доказательство. Знаменатель в левой части формулы (50) не равняется нулю. Действительно, если предположить, что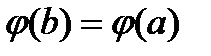 
, то функция 
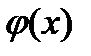удовлетворяет всем условиям теоремы Ролля, а потому для нее нашлась бы такая точка 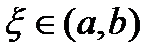, что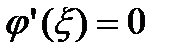 
, что противоречит третьему условию теоремы.
Построим вспомогательную функцию
.
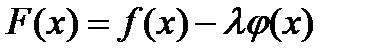Попробуем выбрать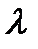 
так, чтоб 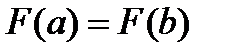. По определению функции 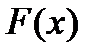это эквивалентно:
,
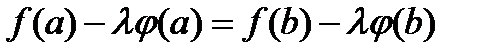откуда, учитывая, что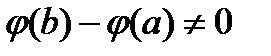 
, получим
,
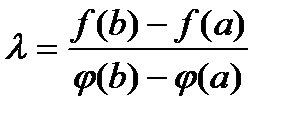а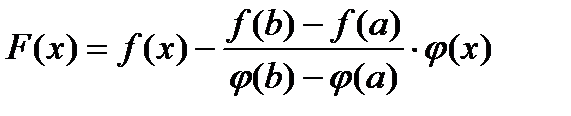 
.
Производная функции 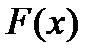определяется следующим образом:
.
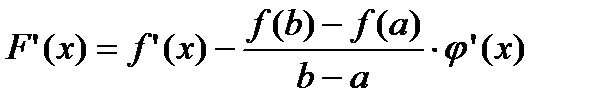Для 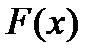выполнены все условия теоремы Ролля, поэтому существует 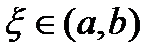, что :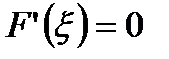
,
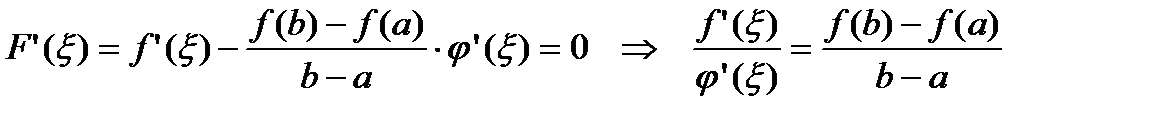что и нужно было доказать.
Замечание. Теорема Лагранжа является частным случаем теоремы Коши при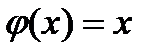 
.
Теорема Дарбу
Определение 3. Будем говорить, что функция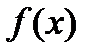 
имеет конечную производную на , если она имеет конечную производную в 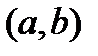, а в точках 
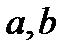имеет конечные односторонние производные.
Пусть функция 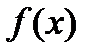имеет конечную производную на некотором промежутке 
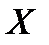. Тогда каждой точке 
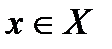можно поставить в соответствие значение 
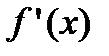, то есть определить функцию:
.
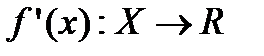Такая функция будет называться функцией производной.
Теорема (Дарбу). Пусть функция 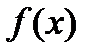имеет конечную производную на 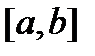. Тогда для 
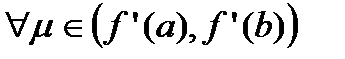найдется такая точка 
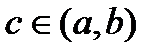, что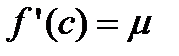 
. Иначе это означает, что функция 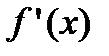не может иметь разрывов І рода.