События
Будем считать, что поводится некоторый эксперимент. Само проведение эксперимента будем называть «испытанием». Результат этого эксперимента будем называть «событием». Если событие происходит при каждом испытании, то его будем называть «достоверным» и обозначать греческой буквой Ω (омега). Если событие не наступает ни при каком испытании, то его будем называть «невозможным» и обозначать символом пустого множества: Æ. Если событие может произойти, а может и не произойти, то его будем называть «случайным» и обозначать большими латинскими буквами: A, B, C, ….
Заметим, что использование символики теории множеств здесь вполне оправдано. Кроме символа пустого множества в дальнейшем будут использоваться равенства и подмножества, знаки операций пересечения, объединения и разности множеств. Так, если события A и B всегда наступают одновременно, то будем записывать A=B. Если наступление события A влечёт за собой наступление события B, то это обозначим как AÌB. Событие, наступающее при одновременном наступлении событий A и B, будем обозначать AÇB. Событие, которое наступает, в тот случае, если произошло хотя бы одно из событий A или B, будем обозначать AÈB. Событие, которое наступает, если событие A произошло и при этом событие B не произошло, обозначим A\B. Аналогом достоверного события Ω в теории множеств является универсальное множество. Противоположным событием для события A будем называть событие Ω\A, которое обозначим чёрточкой наверху: `A=Ω\A (эта операция аналогична дополнению в теории множеств). Справедливы равенства A Ç`A = Æ, A È`A = Ω.
События, которые не могут наступить одновременно, называются «несовместными». Если события A и B несовместны, то AÇB=Æ.
Иногда бывает удобно использовать понятие «элементарного» события. Событие A будем называть элементарным для данного эксперимента, если для любого события B будет справедливым одно из утверждений: AÌB или AÇB=Æ. То есть, либо событие A целиком входит в событие B, либо целиком не входит. Множество, состоящее из всех элементарных событий данного эксперимента, называется «вероятностным пространством».
В качестве примера эксперимента приведём бросание игральной кости (кубика). При таком эксперименте можно фиксировать число очков на его верхней грани. Тогда элементарными событиями будут шесть событий, заключающихся в выпадении единицы, двойки, тройки, четвёрки, пятёрки и шестёрки на верхней грани кубика. Достоверным событием будет «выпадение числа очков меньше семи». Невозможным событием будет выпадение нуля очков. Случайных событий, не являющимся элементарными, достаточно много, например, таким событием является «выпадение числа очков меньше пяти».
Понятие вероятности
Что такое «вероятность»? Это слово часто используется в обыденной жизни. Им обозначают меру уверенности в том, что произойдёт некоторое событие. При этом обычно вероятность выражают в процентах, имея в виду, что если событие обязательно произойдёт, то вероятность этого равна 100%. Так, в прогнозе погоды можно услышать, что вероятность дождя в ближайшие два часа равна 60%.
Разберёмся, что имеется в обычной жизни в виду, когда утверждается, что вероятность события A равна числу р? Попытайтесь сами себе ответить на вопрос: «Что такое вероятность события 60%?» Скорее всего, Ваш ответ будет такой: «Событие произойдёт в 60 случаях из 100». Вы на верном пути. Просто слишком категорично. Неужели Вы всерьёз думаете, что событие произойдёт ровно в 60 случаях из 100? Действительно, такая предопределённость, особенно во время сотого испытания выглядит весьма неправдоподобно. Более верным следует признать такой ответ: «Событие произойдет примерно в 60 случаях из 100». Согласен. Остался другой вопрос: «Что такое примерно 60? Это больше чего и меньше чего?» Не нужно ждать строгих ответов на такие вопросы.
Чтобы окончательно разобраться в том, что такое вероятность с житейской точки зрения, введём понятие частоты появления события. Пусть произведено N испытаний и событие A произошло M раз. Тогда частотой f появления события будем называть дробь M / N. Предположим, что проводимый эксперимент характеризуется устойчивостью частот. Под этим термином подразумевается, что в разных достаточно длинных сериях испытаний, частоты появления события A не сильно отличаются друг от друга. В опытах с такими условиями обычно наблюдается, что чем больше длина серии экспериментов, тем частота появления события ближе к некоторому числу, являющемуся внутренней характеристикой события (которое и называется вероятностью). Если Вы помните тему «пределы» из курса математики, то может быть, Вам пришла мысль о том, что вероятность — это предел частоты, при стремлении числа испытаний к бесконечности. Практически идеально, только опять не надо так категорично. Если бы это было так, то согласно определению предела последовательности, для любого числа ε>0, существовал бы такой номер испытания, начиная с которого, обязательно выполнилось бы неравенство p –ε < f < p +ε. Подобного ограничения не может быть, так как теоретически (но не практически!) частота f может принимать любые, допустимые правилами арифметики, значения. Верным будет утверждение, известное в теории вероятностей под названием «Теорема Бернулли»: для любого числа ε>0 верно, что 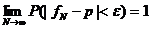 . Здесь fN это частота появления события A в первых N испытаниях. Такое стремление частоты к вероятности математики называют «стремлением по вероятности». Разумеется, это не есть стремление в полном смысле этого слова. В одной из моих любимых книжек (Вентцель Е.С. «Теория вероятностей») для такого стремления используется глагол «приближается». Некоторым недостатком формулировки теоремы Бернулли, выдаваемой здесь за житейский смысл вероятности, является то, что вероятность события определяется через вероятность другого события.
. Здесь fN это частота появления события A в первых N испытаниях. Такое стремление частоты к вероятности математики называют «стремлением по вероятности». Разумеется, это не есть стремление в полном смысле этого слова. В одной из моих любимых книжек (Вентцель Е.С. «Теория вероятностей») для такого стремления используется глагол «приближается». Некоторым недостатком формулировки теоремы Бернулли, выдаваемой здесь за житейский смысл вероятности, является то, что вероятность события определяется через вероятность другого события.
Если Вы согласны с близостью вероятности и частоты при большом количестве испытаний, то теперь можете окончательно сформулировать ответ на вопрос: «Что такое вероятность 60%?» Видимо ответ такой: «При большом числе испытаний частота события приближается, пусть с некоторыми временными отклонениями, к 3/5». Последний вопрос: «А как быть с вероятностью дождя в ближайшие два часа?» Действительно, не может быть и речи о проведении этого эксперимента многократно. Ближайшие два часа пройдут раз и навсегда. Дождь либо будет, что приведёт к частоте, равной единице, либо не будет, и тогда частота этого события окажется равной нулю. В любой ситуации, никакого приближения частоты к вероятности не ожидается. Чтобы решить эту проблему запомните свои ощущения относительно меры уверенности того, что в многократно повторяющемся эксперименте произойдёт событие с аналогичной вероятностью, и перенесите эти ощущения на событие в неповторяемом эксперименте.
Аксиомы вероятности
В математике даётся следующее определение понятия вероятность: каждому событию A ставится в соответствие вещественное число P(A), удовлетворяющее следующим трём аксиомам:
1) Неотрицательность. P(A)³0,
2) Нормированность. P(Ω)=1,
3) Аддитивность (аксиома сложения). Если A i ÇA j =Æ при i ≠ j, то 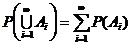 , или то же самое в развёрнутом виде: P(A1ÈA2ÈA3È…ÈA n È…)=P(A1)+P(A2)+P(A3)+…+P(A n)+…. В частности для двух событий: если AÇB=Æ, то P(AÈB)=P(A)+P(B). Или то же самое словами: Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.
, или то же самое в развёрнутом виде: P(A1ÈA2ÈA3È…ÈA n È…)=P(A1)+P(A2)+P(A3)+…+P(A n)+…. В частности для двух событий: если AÇB=Æ, то P(AÈB)=P(A)+P(B). Или то же самое словами: Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.
Теперь возникает закономерный вопрос гуманитария: «Почему так, и какая связь этого с житейским пониманием вероятности». Выше было установлено, что вероятность приближённо равна частоте (при достаточно большом количестве испытаний) и «приближается» к ней при неограниченном увеличении числа испытаний (я всё-таки глагол «приближается» пишу в кавычках, так как ни о какой монотонности убывания величины | f – p | не может быть и речи). И житейские представления о вероятности, кроме как с понятием частоты, связать не с чем. Убедимся в выполнении свойств частоты, соответствующих трём аксиомам вероятности.
1) Частота равна отношению двух неотрицательных чисел (числа наступивших событий и количества испытаний) и не может быть отрицательной.
2) Если событие достоверное, то оно происходит при любом испытании. Число появлений события совпадает с числом экспериментов. Оказываются равными числитель и знаменатель дроби, равной частоте. Поэтому частота появления достоверного события равна единице.
3) Разберём простейший случай. Пусть событий не бесконечно много, а всего два. Пусть поведено N испытаний, событие A произошло K раз, а событие B наступило L раз. Причём, поскольку A и B несовместные события, то одновременно они произойти не могли, и, следовательно, хотя бы одно из этих событий наступило столько же раз, сколько наступило ровно одно из них, то есть (K + L) раз. Тогда частота наступления события A равна K / N, частота наступления события B равна L / N, а частота наступления хотя бы одного из этих событий равна (K + L)/ N. И действительно справедливо равенство K / N + L / N =(K + L)/ N.
Теперь остаётся надеяться (а математик аксиомы постулирует, не испытывая никаких психологических проблем), что у вероятности свойства такие же как и у частоты.
Следствия из аксиом вероятности
1. Вероятность противоположного события P(`A) = 1 – P(A).
Доказательство. Поскольку A Ç`A = Æ и A È`A = Ω, то по нормированности вероятности и аксиоме сложения: 1 = P(Ω) = P(A È`A) = P(A) + P(`A). Следовательно P(`A) = 1 – P(A), как впрочем и P(A) = 1– P(`A). Это свойство часто используется при нахождении вероятностей реализации хотя бы одного из некоторого набора событий. Обычно гораздо проще найти вероятность противоположного события (заключающееся в том, что должны будут одновременно реализоваться все события из этого набора) и вычесть её из единицы.
2. Вероятность невозможного события P(Æ)=0.
 Доказательство. Поскольку Æ = Ω\Ω =`Ω, то по вероятности противоположного события P(`Ω)=1 – P(Ω)=1–1=0.
Доказательство. Поскольку Æ = Ω\Ω =`Ω, то по вероятности противоположного события P(`Ω)=1 – P(Ω)=1–1=0.
3. Монотонность вероятности. Если AÌB, то P(A) ≤ P(B).
Доказательство. Разобьём событие B на два несовместных события A и B\A (см. рис. 1). Теперь из AÇ(B\A)=Æ и AÇ(B\A)=B по аксиоме сложения следует, что P(B)=P(A)+P(B\A). Но по неотрицательности вероятности P(B\A) ≥ 0 и поэтому P(B) = P(A) + P(B\A) ≥ P(A) + 0 = P(A). Это свойство названо монотонностью, поскольку напоминает определение возрастающей функции на промежутке, согласно которому большему значению аргумента соответствует большее значение функции.
4. Ограниченность вероятности. P(A) ≤ 1.
Доказательство. Любое событие AÌΩ. По свойству монотонности и аксиоме нормированности P(A) ≤ P(Ω) = 1.
5.  Правило сложения. P(AÈB)=P(A)+P(B)–P(AÇB). В отличие от аксиомы сложения здесь события A и B какие угодно (в аксиоме сложения они были обязательно несовместные).
Правило сложения. P(AÈB)=P(A)+P(B)–P(AÇB). В отличие от аксиомы сложения здесь события A и B какие угодно (в аксиоме сложения они были обязательно несовместные).
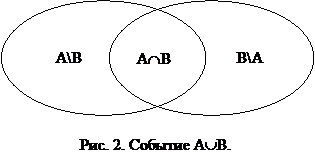
Доказательство. Разобьём событие AÈB на три несовместных события A\B, B\A и AÇB (см. рис. 2). Теперь из того, что AÈB=(A\B)È(B\A)È(AÇB), и попарной несовместности этих трёх событий, то есть из того, что (A\B)Ç(B\A)=Æ, (A\B)Ç(AÈB)=Æ и (B\A)Ç(AÈB)=Æ, согласно аксиоме сложения следует, что P(AÈB)=P(A\B)+P(B\A)+P(AÇB). Заметим, что при этом разбиении, событие A автоматически окажется разбитым на два несовместных события: A\B и AÇB. И из того, что (A\B)Ç(AÇB)=Æ и A=(A\B)È(AÇB) по аксиоме сложения следует, что P(A)=P(A\B)+P(AÇB). Аналогичное явление произойдёт и с событием B. Оно тоже будет разбито на два несовместных события: B\A и AÇB. И из того, что (B\A)Ç(AÇB)=Æ и B=(B\A)È(AÇB) по аксиоме сложения следует, что P(B)=P(B\A)+P(AÇB). Теперь из трёх полученных равенств с помощью арифметики можно доказать требуемое утверждение: 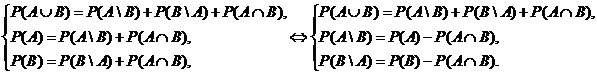 Подставляя второе и третье равенства, в первое, получим
Подставляя второе и третье равенства, в первое, получим
P(AÈB)=P(A)–P(AÇB)+P(B)–P(AÇB)+ P(AÇB)= P(A)+P(B)–P(AÇB).
6. Неравенство для совокупности событий. 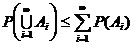 , или то же самое в развёрнутом виде: P(A1ÈA2ÈA3È…ÈAnÈ…) ≤ P(A1)+P(A2)+P(A3)+…+P(An)+…. В частности для двух событий: P(AÈB) ≤ P(A)+P(B).
, или то же самое в развёрнутом виде: P(A1ÈA2ÈA3È…ÈAnÈ…) ≤ P(A1)+P(A2)+P(A3)+…+P(An)+…. В частности для двух событий: P(AÈB) ≤ P(A)+P(B).
Доказательство проведём только для двух событий. По правилу сложения P(AÈB)=P(A)+P(B)–P(AÇB). По неотрицательности вероятности P(AÇB) ≥ 0. Следовательно, P(AÈB)=P(A)+P(B)–P(AÇB) ≤ P(A)+P(B)–0=P(A)+P(B). Напомним, что равенство наступает при AÇB=Æ.
Классический способ вычисления вероятностей
Пусть при проведении эксперимента возможно появление n различных элементарных событий. Обозначим их ω1, ω2, ω3, …, ω n. Таким образом, они оказываются попарно несовместными (при i ≠ j ω i Çω j =Æ) и единственно возможными (ω1Èω2Èω3È…Èω n =Ω). По аксиоме сложения P(ω1)+P(ω2)+P(ω3)+…+P(ω n)=P(ω1Èω2Èω3È…Èω n)=P(Ω)=1. Если теперь предположить, что события ω1, ω2, ω3, …, ω n равновозможные, то их вероятности логично считать равными друг другу: P(ω1)=P(ω2)=P(ω3)= … =P(ω n). И поэтому сумма их вероятностей — это сумма равных друг другу n слагаемых:
1 = P(ω1) + P(ω2) + P(ω3) + … + P(ω n) = P(ω1) + P(ω1) + P(ω1) + … + P(ω1) = n P(ω1). Следовательно, P(ω1)=1/ n. Как впрочем и все остальные: P(ω1)=P(ω2)=P(ω3)=… =P(ω n)=1/ n. Пусть событие A состоит из m элементарных событий, для конкретности первых m: A=ω1Èω2Èω3È…Èω m. По аксиоме сложения вероятность события A будет равна сумме m одинаковых слагаемых: P(A)=P(ω1)+P(ω2)+P(ω3)+…+P(ω m)=1/ n +1/ n +1/ n +…+1/ n = m ∙(1/ n)= m / n. Если события ω1, ω2, ω3, …, ω n не будут равновозможными, то нельзя их вероятности считать равными друг другу и выведенная формула не будет справедливой. Равновозможность событий ω1, ω2, ω3, …, ω n обычно следует из симметричности задачи. Например, если игральная кость сделана без смещённого центра тяжести, то нет оснований предпочесть какую-то из её граней другим. Для игральной кости P(ω1)=P(ω2)=P(ω3)=P(ω4)=P(ω5)=P(ω6)=1/6. Существуют и другие объекты, обладающие свойством симметрии. Простейшим из них является монета (если не оговорено, что она гнутая). При подбрасывании монеты возможны два исхода: выпадение герба и выпадение решётки на её верхней грани. Для симметричной монеты P(ω1)=P(ω2)=1/2. Можно организовать эксперимент с любым заранее данным числом n равновозможных исходов. Для этого можно взять колоду из n карт, перемешать её и наугад выбрать одну карту. Тот же эффект достигается, если n различных шариков поместить в урну, и вытащить один из них не глядя.
Геометрический способ вычисления вероятностей
Пусть эксперимент состоит из бросания точки x на промежуток [ a; b), причём вероятность попадания этой точки в любые промежутки равной длины, являющиеся его частями одинаковая. Исследуем вероятности попадания точки в два промежутка различной длины. Обозначим эти длины l 1 и l 2. Пусть отношение длин этих промежутков равно отношению двух целых чисел: l 1/ l 2= k 1/ k 2. Тогда по свойству пропорции l 1/ k 1= l 2/ k 2= m. Здесь m имеет смысл длины k 1 непересекающихся промежутков, составляющих промежуток длины l 1 и k 2 непересекающихся промежутков, составляющих промежуток длины l 2. Пусть вероятность попадания в промежуток длины m равна p. Тогда по аксиоме сложения вероятности попадания в промежутки длин l 1 и l 2 соответственно равны pk 1 и pk 2. И отношение этих вероятностей окажется равной отношению длин промежутков: pk 1/(pk 2)= l 1/ l 2. Логично предположить, что этим свойством обладают и промежутки, отношение длин которых нельзя выразить рациональным числом (любое иррациональное число можно представить как предел последовательности рациональных чисел), то есть вероятность попадания в промежуток при вышеупомянутом условии всегда пропорциональна его длине. Поскольку попадание точки x в промежуток [ a; b) событие достоверное, то вероятность этого равна единице. И, следовательно, для любого промежутка [ c; d)Ì[ a; b) справедливо:  .
.
Полученная формула позволяет обнаружить «парадокс нулевой вероятности» заключающийся в существовании событий, не являющихся невозможными, но тем не менее вероятности которых равны нулю (такие события называются «почти невозможными»). Действительно, если поставить вопрос о попадании точки x в точку c (это событие возможно), которую можно трактовать как предельное состояние промежутка [ c; d) при d стремящимся к c, то  . Если развивать эту мысль дальше, то окажется, что отрезок, на который точка неизбежно упадёт, состоит только из таких точек, вероятности попадания в которые равны нулю. И, следовательно, в первом же эксперименте (как впрочем и во всех остальных) обязательно произойдёт почти невозможное событие! По теореме Бернулли при p =0 для любых чисел ε>0 и δ>0 существует номер испытания, начиная с которого P(f < ε) > 1–δ. Здесь частота f вовсе не обязательно равна нулю. Из этой теоремы следует, что при неограниченном увеличении числа опытов, частота почти невозможного события, опустится ниже любого, наперёд заданного значения со сколь угодно большой вероятностью. Если перейти от теоретических бесед к практике (источнике здравого смысла) и пытаться получить почти невозможное событие в опыте, то для фиксации такого события придётся обзавестись измерительным прибором бесконечной точности, что невозможно.
. Если развивать эту мысль дальше, то окажется, что отрезок, на который точка неизбежно упадёт, состоит только из таких точек, вероятности попадания в которые равны нулю. И, следовательно, в первом же эксперименте (как впрочем и во всех остальных) обязательно произойдёт почти невозможное событие! По теореме Бернулли при p =0 для любых чисел ε>0 и δ>0 существует номер испытания, начиная с которого P(f < ε) > 1–δ. Здесь частота f вовсе не обязательно равна нулю. Из этой теоремы следует, что при неограниченном увеличении числа опытов, частота почти невозможного события, опустится ниже любого, наперёд заданного значения со сколь угодно большой вероятностью. Если перейти от теоретических бесед к практике (источнике здравого смысла) и пытаться получить почти невозможное событие в опыте, то для фиксации такого события придётся обзавестись измерительным прибором бесконечной точности, что невозможно.
Естественно ожидать, что существуют и события с вероятностью равной единице, не являющиеся достоверными. Их называют «почти достоверными». Это события, противоположные почти невозможным событиям. Например, это событие x Î[ a; c)È(c; b).
Как организовать эксперимент с бросанием точки на отрезок, именно так, чтобы вероятность попадания этой точки в любые промежутки равной длины, одинаковая? Можно предложить нанести числа от a до b на обод велосипедного колеса (при этом концы промежутка, числа a и b, геометрически будут находиться в одной точке обода, именно по этой причине один из концов промежутка в него не был включён), поднять колесо над поверхностью земли, раскрутить его, и в случайно выбранный момент нажать на тормоз. То число, которое окажется напротив тормозной колодки и определит точку x.
Геометрическим способом можно также определить вероятность попадания точки на часть плоской фигуры, при условии, что вероятности попадания этой точки в любые фрагменты фигуры равной площади одинаковые. В этом случае вероятность будет равна отношению площади части фигуры к площади всей фигуры.
Условная вероятность
Вероятность события A при условии, что произошло событие B, называется «условной вероятностью» и обозначается P(A|B). Рассмотрим только случай, когда P(B) > 0 (даже если событие B произошло, то в силу парадокса нулевой вероятности, ещё нет оснований полагать, что P(B) ≠ 0). В математике даётся следующее определение понятия условной вероятности при P(B) > 0: 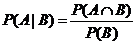 . Это очень странное заявление для представителей гуманитарных наук. Действительно, если словесное описание дано, то как можно постулировать формулу? Она должна быть выведена из словесного описания! Или наоборот: почему эта формула равна вероятности события A при условии, что событие B произошло?
. Это очень странное заявление для представителей гуманитарных наук. Действительно, если словесное описание дано, то как можно постулировать формулу? Она должна быть выведена из словесного описания! Или наоборот: почему эта формула равна вероятности события A при условии, что событие B произошло?
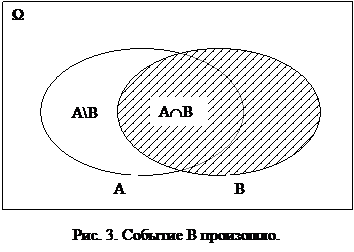 Посмотрите на рисунок 3. На нём большим прямоугольником обозначено достоверное событие Ω, а эллипсами случайные события A и B. Если принять за факт, что событие B произошло, то теперь уже оно начинает играть роль достоверного события. Для случаев, когда вероятность можно вычислить классическим (на основании равновозможности элементарных событий) или геометрическим способами, можно доказать, что отношения друг к другу вероятностей различных событий, влекущих за собой наступление события B (в частности событий AÇB и собственно B), остаются неизменными. Будем надеяться, что это свойство остаётся справедливым и для других экспериментов, вероятности событий в которых нельзя вычислить ни с помощью классического ни с помощью геометрического способов. Тогда получим:
Посмотрите на рисунок 3. На нём большим прямоугольником обозначено достоверное событие Ω, а эллипсами случайные события A и B. Если принять за факт, что событие B произошло, то теперь уже оно начинает играть роль достоверного события. Для случаев, когда вероятность можно вычислить классическим (на основании равновозможности элементарных событий) или геометрическим способами, можно доказать, что отношения друг к другу вероятностей различных событий, влекущих за собой наступление события B (в частности событий AÇB и собственно B), остаются неизменными. Будем надеяться, что это свойство остаётся справедливым и для других экспериментов, вероятности событий в которых нельзя вычислить ни с помощью классического ни с помощью геометрического способов. Тогда получим:  . В этих равенствах использовано, что при наступлении события B, говорить о наступлении события A и события AÇB то же самое, поскольку оставшаяся часть (A\B) события A никак уже произойти не сможет, и поэтому действительно P((AÇB)|B)=P(A|B).
. В этих равенствах использовано, что при наступлении события B, говорить о наступлении события A и события AÇB то же самое, поскольку оставшаяся часть (A\B) события A никак уже произойти не сможет, и поэтому действительно P((AÇB)|B)=P(A|B).
Вернёмся к случаю P(B) = 0. Условная вероятность P(A|B) (с точки зрения математика она не определена), с точки зрения гуманитария, равна вероятности события A при условии, что произошло событие B. Напомним, что вероятность в житейском понимании определяется через частоту появления события в эксперименте при стремлении числа испытаний (которое будет равно числу появления события B) к бесконечности. Теперь вопрос: как организовать эксперимент, чтобы в нём событие B с нулевой вероятностью произошло бесконечное число раз, при отсутствии технической возможности зафиксировать такое событие?
Правило произведения
Из равенства, служащего определением условной вероятности 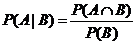 следует формула: P(AÇB)=P(A|B)∙P(B). Её называют «правило произведения». Она используется для нахождения вероятности одновременной реализации двух событий. Сначала вычисляется вероятность какого-то одного из этих событий, а потом, вообразив, что первое событие уже произошло, находят вероятность второго события. Перемножая эти две вероятности, получают окончательный результат.
следует формула: P(AÇB)=P(A|B)∙P(B). Её называют «правило произведения». Она используется для нахождения вероятности одновременной реализации двух событий. Сначала вычисляется вероятность какого-то одного из этих событий, а потом, вообразив, что первое событие уже произошло, находят вероятность второго события. Перемножая эти две вероятности, получают окончательный результат.
Формула полной вероятности
Рассмотрим двухступенчатый эксперимент, в котором на первой стадии обязательно происходит ровно одно из n событий: H1, H2, H3, …, H n (буква H — это первая буква в слове «гипотеза»). Для этого эти n событий должны быть попарно несовместными (при i ≠ j H i ÇH j =Æ) и единственно возможными (H1ÈH2ÈH3È…ÈH n =Ω) событиями. На второй стадии эксперимента, после того как уже одно из событий H i произошло, происходит или не происходит событие A. Схема опыта изображена на рисунке 4.
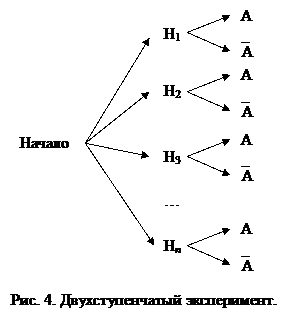 Представим событие A в виде объединения непересекающихся событий: A=AÇΩ=AÇ(H1ÈH2ÈH3È…ÈH n)=(AÇH1)È (AÇH2)È(AÇH3)È …È(AÇH n) (на рисунке 5 показано разложение события A, обозначенного эллипсом). По аксиоме сложения вероятностей имеем: P(A) = P(AÇH1) + P(AÇH2) + + P(AÇH3) + … + P(AÇH n).
Представим событие A в виде объединения непересекающихся событий: A=AÇΩ=AÇ(H1ÈH2ÈH3È…ÈH n)=(AÇH1)È (AÇH2)È(AÇH3)È …È(AÇH n) (на рисунке 5 показано разложение события A, обозначенного эллипсом). По аксиоме сложения вероятностей имеем: P(A) = P(AÇH1) + P(AÇH2) + + P(AÇH3) + … + P(AÇH n).
Если все события H i имеют ненулевые вероятности (иначе не записать условные вероятности), то используя правило произведения для каждого слагаемого получим: P(A)=P(A|H1)·P(H1)+P(A|H2)·P(H2)+ +P(A|H3)·P(H3)+…+P(A|H n)·P(H n). Выведенная формула называется «формулой полной вероятности».
Формула гипотез (Байеса)
 Пусть завершился двухступенчатый эксперимент, описанный в предыдущем пункте. Пусть на его второй стадии произошло событие A. Предположим, что P(A)¹0 (иначе не записать условную вероятность). Поставим вопрос: какова условная вероятность того, что на первой стадии эксперимента произошло событие H k (где k =1, 2, 3, …, n)? Эта условная вероятность P(H k |A) называется «апостериорной», в отличие от вероятности P(H k), которая называется «априорной». Эти две вероятности одного и того же события могут отличаться друг от друга, поскольку априорная вероятность вычисляется до эксперимента, а апостериорная после, когда уже появилась дополнительная информация, используя которую возможно скорректировать вероятность события H k. По формуле, являющейся определением условной вероятности, имеем:
Пусть завершился двухступенчатый эксперимент, описанный в предыдущем пункте. Пусть на его второй стадии произошло событие A. Предположим, что P(A)¹0 (иначе не записать условную вероятность). Поставим вопрос: какова условная вероятность того, что на первой стадии эксперимента произошло событие H k (где k =1, 2, 3, …, n)? Эта условная вероятность P(H k |A) называется «апостериорной», в отличие от вероятности P(H k), которая называется «априорной». Эти две вероятности одного и того же события могут отличаться друг от друга, поскольку априорная вероятность вычисляется до эксперимента, а апостериорная после, когда уже появилась дополнительная информация, используя которую возможно скорректировать вероятность события H k. По формуле, являющейся определением условной вероятности, имеем: 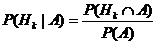 . Теперь числитель этой дроби преобразуем по правилу произведения, а знаменатель по формуле полной вероятности:
. Теперь числитель этой дроби преобразуем по правилу произведения, а знаменатель по формуле полной вероятности:  . Выведенная формула называется «формулой Байеса».
. Выведенная формула называется «формулой Байеса».
Независимость двух событий
В математике даётся следующее определение независимости событий: «два события A и B называются независимыми, если P(AÇB)=P(A)∙P(B)».
Что такое, с точки зрения здравого смысла, независимость события A от события B? Это означает, что вероятность события A никак не изменится, если произойдёт событие B. На языке формул это выглядит следующим образом: P(A)=P(A|B). В записи этого соотношения использована условная вероятность, поэтому придётся предположить, что P(B)¹0.
Используя формулу (при P(B)¹0), служащую определением условной вероятности получим: 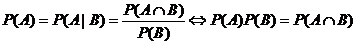 . Действительно, получилось соотношение, которое было дано в определении. Интересно, что в него события A и B входят симметрично. Действительно произведение не меняется, если переставить местами сомножители. Аналогичным свойством обладает и фраза об одновременном появлении событий. Если предположить, что и P(A)¹0, то по правилу произведения можно записать: P(A)∙P(B)=P(AÇB)=P(BÇA)=P(B|A)∙P(A). Сокращая это равенство на P(A)¹0, получим: P(B)=P(B|A). То есть, вероятность события B тоже не изменяется в зависимости от того, произошло ли событие A. Таким образом, если P(A)¹0 и P(B)¹0, то независимость событий A и B друг от друга может быть только двусторонней: если событие A не зависит от события B, то и событие B не зависит от события A.
. Действительно, получилось соотношение, которое было дано в определении. Интересно, что в него события A и B входят симметрично. Действительно произведение не меняется, если переставить местами сомножители. Аналогичным свойством обладает и фраза об одновременном появлении событий. Если предположить, что и P(A)¹0, то по правилу произведения можно записать: P(A)∙P(B)=P(AÇB)=P(BÇA)=P(B|A)∙P(A). Сокращая это равенство на P(A)¹0, получим: P(B)=P(B|A). То есть, вероятность события B тоже не изменяется в зависимости от того, произошло ли событие A. Таким образом, если P(A)¹0 и P(B)¹0, то независимость событий A и B друг от друга может быть только двусторонней: если событие A не зависит от события B, то и событие B не зависит от события A.
Заметим, что определение независимости событий формально можно применять и для событий с нулевой вероятностью, но при этом будет невозможно сравнить результат с соображениями здравого смысла, поскольку они оперируют понятием условной вероятности.
Свойства независимых событий
1.  Если события A и B независимые, то и события A и`B тоже независимые.
Если события A и B независимые, то и события A и`B тоже независимые.
Доказательство. Представим событие B в виде объединения несовместных событий (см. рис. 6): B=ΩÇB=(AÈ`A)ÇB=(AÇB)È È(`AÇB). Тогда по аксиоме сложения P(B)=P(AÇB)+P(`AÇB). Из независимости событий A и B следует, что P(AÇB)=P(A)×P(B). Подставляя это равенство в предыдущее, учитывая свойство вероятности противоположного события, получим: P(B)=P(A)×P(B)+P(`AÇB)ÛP(B)–P(A)×P(B)=P(`AÇB)Û ÛP(B)×(1–P(A))=P(`AÇB)ÛP(B)×P(`A)=P(`AÇB). Последнее равенство и доказывает независимость событий A и`B.
2. Если P(A)=0, то событие A независимо с любым событием.
Доказательство. Пусть вероятность события B равна нулю: P(B)=0. Для этого оно должно быть либо невозможным, либо почти невозможным. Заметим, что (AÇB)ÌB и по аксиоме неотрицательности и свойству монотонности вероятности: 0≤P(AÇB)≤P(B)=0, и, следовательно, P(AÇB)=0. Тогда P(AÇB)=P(A)×P(B)Û Û0=P(A)×0 Û 0=0 верное равенство, что и доказывает независимость событий A и B. С философской точки зрения так и должно быть: невозможное событие никогда не происходит, и вполне естественно, что оно ни от чего не может зависеть и от него ничего не может зависеть.
3. Если P(A)=1, то событие A независимо с любым событием.
Доказательство. Пусть вероятность события B равна единице: P(B)=1. Для этого оно должно быть либо достоверным, либо почти достоверным. По свойству вероятности противоположного события P(`B)=1–P(B)=1–1=0. Тогда по предыдущему свойству события A и `B независимые. А поскольку противоположным к событию `B является событие B, то первому из этих свойств события A и B независимые. Действительно достоверное событие происходит при любом испытании независимо ни от чего. Естественно, что и от него ничего не может зависеть.
4. Если события с ненулевыми вероятностями независимые, то они совместные.
Доказательство. Пусть события A и B независимые, то есть P(AÇB)=P(A)×P(B), а по условию P(A)>0 и P(B)>0. Поэтому P(AÇB)>0, и, следовательно, событие AÇB не может быть несовместным (иначе бы его вероятность была бы равна нулю).
5. Если события с ненулевыми вероятностями несовместные, то они зависимые.
Доказательство. Пусть события A и B несовместные, то есть AÇB=Æ. Тогда P(AÇB)=0. По условию P(A)>0 и P(B)>0. Следовательно, P(A)×P(B)>0, и поэтому равенство P(AÇB)=P(A)×P(B) невозможно, то есть события A и B не являются независимыми.
6. Если события с ненулевыми вероятностями противоположные, то они зависимые.
Доказательство. Если события противоположные, то они обязательно несовместные и это свойство следует из предыдущего.
Независимость трех и более событий
Если событий три или больше, то различают два вида независимости: попарную и взаимную.
События A1, A2, A3, …, A n называются попарно независимыми, если независимы события в каждой из пар этих событий, то есть для любых i ¹ j верно, что P(A i ÇA j)=P(A i)×P(A j). В частности, три события A, B и C будут попарно независимыми, если 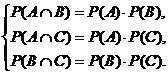
События A1, A2, A3, …, A n называются взаимно независимыми (или независимыми в совокупности), если для любого набора из этих n событий верно, что вероятность их одновременного появления равна произведению их вероятностей. В частности, три события A, B и C будут взаимно независимыми, если 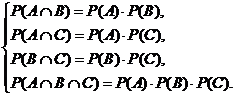
Из этих двух определений следует, что если события взаимно независимые, то они обязательно попарно независимые. Действительно, если что-то верно для любого набора, то это верно в том числе и для любой пары. Поэтому, когда употребляют термин «независимые события» без уточнения как именно независимые, то следует понимать, что они взаимно независимые. Разберём, что такое взаимная независимость событий с точки зрения здравого смысла на примере трёх событий. Если событие A не зависит от появления любой комбинации событий B и C, то кроме независимости от событий B и C это ещё означает независимость от события BÇC. Другими словами: должно ещё выполняться равенство P(A)=P(A|BÇC). Учитывая определение условной вероятности получим 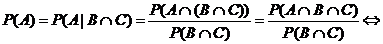 P(AÇBÇC)= =P(A)∙P(BÇC)=P(A)∙P(B)∙P(C). Действительно, данное определение совпадает с представлениями о независимости, следующими из здравого смысла.
P(AÇBÇC)= =P(A)∙P(BÇC)=P(A)∙P(B)∙P(C). Действительно, данное определение совпадает с представлениями о независимости, следующими из здравого смысла.
Рассмотрим ещё один вопрос: если из взаимной независимости следует попарная, то не следует ли из попарной взаимная? Правильный ответ: нет, не следует. Чтобы доказать это достаточно привести хотя бы один пример трёх попарно независимых событий, которые не являются взаимно независимыми. Такой пример был найден советским математиком Бернштейном. Он предложил взять тетраэдр (тетраэдр — это правильная объёмная фигура, состоящая из четырёх одинаковых равносторонних треугольников) и покрасить одну его сторону в красный цвет, другую в синий, третью в зелёный, а на четвёртую частично разукрасить в красный цвет, частично в синий и частично в зелёный (см. рис. 7).
Экспериментом будет подбрасывание тетраэдра с фиксацией нижней грани после падения. Пусть событие A: «на оказавшейся внизу грани присутствует красный цвет», событие B: «на оказавшейся внизу грани присутствует синий цвет» и событие C: «на оказавшейся внизу грани присутствует зелёный цвет». Тогда событиями AÇB, AÇC, BÇC и AÇBÇC будет событие: «на оказавшейся внизу грани присутствуют все три цвета». В силу симметрии тетраэдра возможно использование классического способа вычисления вероятностей, согласно которому вероятности того, что тетраэдр упадёт на каждую из четырех граней, равны друг другу и равны ¼. Для реализации каждого из событий A, B и C возможно два способа: тетраэдр упадёт на грань, целиком закрашенную в соответствующий цвет, и на грань, содержащую все три цвета. Поэтому P(A)=P(B)=P(C)=2/4=1/2. А вероятности одновременной реализации любой комбинации этих трёх событий равны: P(AÇB)=P(AÇC)=P(BÇC)=P(AÇBÇC)=1/4. Очевидно, что выполняются три равенства, обеспечивающие попарную независимость событий A, B и C: 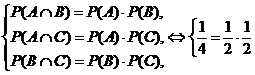 . А четвёртое равенство, которое как раз и позволяет отличить взаимную независимость от попарной не выполнятся:
. А четвёртое равенство, которое как раз и позволяет отличить взаимную независимость от попарной не выполнятся: 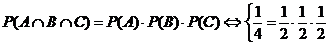 , поскольку
, поскольку 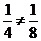 . Поэтому введённые события A, B и C попарно независимые, но не взаимно независимые. Если интуиция подсказывала Вам, что события A, B и C не должны были быть даже попарно независимыми, то могу сказать, что интуиция Вас не подвела. Попарная независимость не более чем арифметический фокус, и если бы бросаемая фигура не была бы симметричной, никакой независимости бы не было.
. Поэтому введённые события A, B и C попарно независимые, но не взаимно независимые. Если интуиция подсказывала Вам, что события A, B и C не должны были быть даже попарно независимыми, то могу сказать, что интуиция Вас не подвела. Попарная независимость не более чем арифметический фокус, и если бы бросаемая фигура не была бы симметричной, никакой независимости бы не было.
Последовательность независимых испытаний с двумя исходами
Рассмотрим эксперимент, заключающийся в подбрасывании несимметричной монеты. У несимметричной монеты (в отличие от симметричной) вероятности появления герба и решётки не обязательно равны. Обозначим вероятность выпадения герба p, а решётки q. Поскольку эти события несовместны, и монета обязательно упадёт либо на герб, либо на решётку, то справедливо равенство p + q =1 Û q =1- p. С точки зрения здравого смысла, рассматриваемые события независимые, то есть результат каждого подбрасывания монеты никак не зависит от результатов других подбрасываний в любых комбинациях. Выводы, полученные в этом пункте, окажутся справедливыми и для других экспериментов с двумя исходами, характеризующимися неизменностью вероятностей событий и взаимной независимостью испытаний. Исторически сложилось, что подобная задача родилась при составлении математической модели азартной игры. Это привело к появлению специфической терминологии. Событие, вероятность которого равна p называется «успехом», а противоположное ему событие «неудачей».
Обычно задача ставится так: «какова вероятность того, что произойдёт ровно m успехов в серии из n независимых испытаний?» Эту величину обозначают P n (m). Для решения этой проблемы ответим на пару вопросов:
1. Сколько всего существует элементарных событий, которые соответствуют появлению m успехов в n испытаниях?
На этот вопрос отвечает раздел математики, называемый «комбинаторика». Доказано, что количество способов выбрать m элементов из n без учёта порядка выбора (это как раз нужная ситуация: выбираются номера испытаний, в которых будут зафиксированы успехи; при этом порядок выбора не важен) равно числу сочетаний, которое обозначается 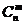 , и может быть найдено по формуле:
, и может быть найдено по формуле:  .
.
2. Какова вероятность каждого из таких элементарных событий?
Поскольку успехов должно быть m (вероятность появления каждого равна p), а число испытаний n, то число неудач должно быть равно (n - m), при этом вероятность неудачи известна и равна q. По правилу произведения для взаимно независимых событий получим произведение m со