МЕЖВУЗОВСКОЙ ОЛИМПИАДЫ ПО ФИЗИКЕ 2013

ЗАДАЧИ С РЕШЕНИЯМИ

(11 апреля 2013 года, СПбГЭТУ «ЛЭТИ»)

1. По вертикально стоящей гладкой и жёсткой спирали скользит гайка, имеющая момент инерции J и массу m. Шаг спирали (расстояние между двумя соседними витками) h. В начальный момент времени гайка покоится. За какое время гайка опустится на расстояние H? (H > h).

Решение: Гайка имеет лишь одну степень свободы, т.к. её поступательное движение и вращательное движение связаны. Вертикальное перемещение D x при повороте на угол Dj находим из условия 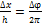, что дает связь соответствующих линейной v и угловых скоростей .

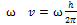При отсутствии трения закон сохранения энергии имеет вид: 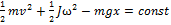. Отсюда находим выражение для скорости гайки: .

, .
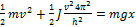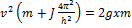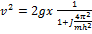Дифференцируя по времени, получим: 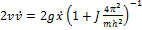, , 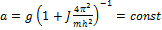следовательно, , , , .

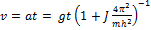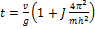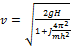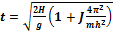2. Велосипедист едет со скоростью v по горизонтальной дороге на велосипеде без крыльев. На какую максимальную высоту h может быть заброшена вверх грязь, срывающаяся с колёс велосипеда? Указать положение той точки на покрышке колеса, с которой при данной скорости движения велосипеда грязь будет забрасываться выше всего. Радиус колеса R. При решении задачи учесть то обстоятельство, что для типичных значений R » 35 см и v » 18 км/ч отношение Rg / v ² < 1, g – ускорение свободного падения. Сопротивление воздуха движению отброшенной вверх грязи не учитывать.

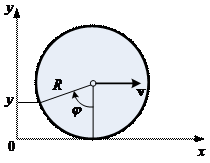Решение. Координата y произвольной точки на ободе колеса может быть записана выражением 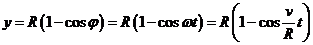(рис.),

откуда 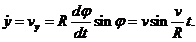Величины 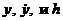связаны соотношением 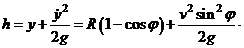Максимальную высоту определим из условия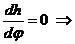 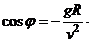Отсюда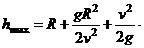

Для исходных численных данных получаем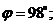

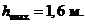
3. Внутри неподвижной сферической чашки радиуса R может двигаться тонкий стержень длины l < 2 R, так что он остается в вертикальной плоскости, проходящей через центр сферы (см. рис.). Если пренебречь трением, то стержень совершает незатухающие колебания. Определите их частоту.

Решение:

Здесь мы имеем пример задачи, в которой из закона сохранения дифференцированием можно получить уравнение движения. Запишем уравнение свободных колебаний в канонической форме .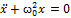

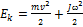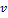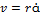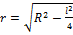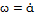В данном случае выполняется закон сохранения энергии. Запишем кинетическую энергию по формуле Кенига: , где – скорость центра масс, J – момент инерции относительно оси, проходящей через центр масс. Учитывая, что , где , и 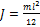. Находим 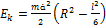. Потенциальную энергию определим по высоте центра тяжести над положением равновесия: .

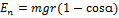Если рассматриваются малые колебания, то 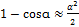, и закон сохранения энергии имеет вид:

.

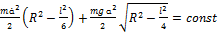Дифференцируя это выражение по времени и записывая полученный результат в форме канонического уравнения колебаний, находим

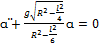. Откуда определяем циклическую частоту колебаний: .

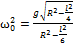4. Термически изолированный цилиндрический сосуд разделён легким подвижным поршнем на две части A и B, в которых находится по одному молю идеального одноатомного газа. В начальный момент температура газа в объёме A равна T_A = T, а в объёме B – T_B = nT. Какую полезную работу могла бы совершить система при условии, что передача тепла от одного объёма к другому полностью обратима?

Решение: Максимально полезную работу можно рассчитать по разности внутренней энергии в начальном и конечном состоянии:

, (*)

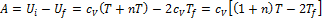Где 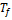– конечная температура системы. Если передача тепла происходит обратимо, а вся система находится в адиабатической оболочке, то её энтропия остается постоянной. Из этого условия можно определить конечную температуру системы 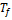. Для каждого объёма

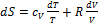, отсюда находим .

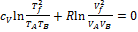Где – объем, занимаемый каждой частью газа после выполнения всей работы, т.е. 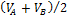, , 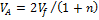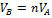. Следовательно,

,

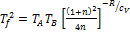Учитывая, что газ одноатомный 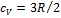, находим 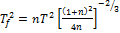. Откуда, используя (*), получаем окончательный ответ: .

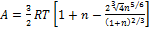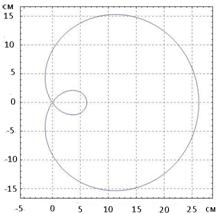5. На рисунке изображена эквипотенциальная линия с потенциалом 9∙10⁵ В для электрического поля, созданного двумя точечными зарядами q ₁ = 20мкКл и q ₂ = –5мкКл. Определить координаты зарядов.

Решение: Силовые линии электрического поля перпендикулярны эквипотенциальной поверхности. В окрестности точки (0,0) однозначное проведение силовой линии невозможно. Следовательно, напряжённость равна нулю. Условие равенства нулю напряжённости поля в точке (0,0):

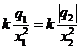(1)

Равенство потенциала в этой точке заданному в условии задачи значению:

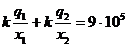(2)

Решая уравнения (1) и (2), получим x ₁ = 10 см; x ₂ = 5 см.

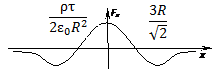6. Тонкое проволочное кольцо радиусом R равномерно заряжено с линейной плотностью зарядов t. Примем ось кольца за ось Х, с началом в центре кольца. Поместим в произвольную точку оси Х точечный диполь с электрическим моментом р, направленным параллельно этой оси. Найдите функциональную зависимость силы, действующей на диполь от координаты х, и постройте примерный график этой зависимости.

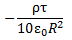Решение. 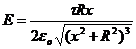; 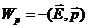, Þ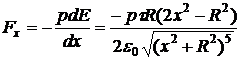

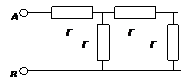7. Вычислите сопротивление между точками А и В бесконечной электрической цепи (см. рисунок), если все сопротивления в цепи одинаковы и равны r.

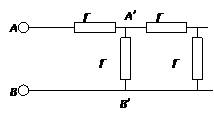Решение:

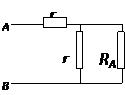Задача имеет решение, поскольку при добавлении нового звена сопротивление между точками А и В падает. При этом искомое сопротивление R _AB не превышает сопротивления одного звена, которое равно 2 r, но больше сопротивления одного резистора r: r < R _AB < 2 r.

Поскольку цепь бесконечная, сопротивление между точками А’ и В’ также равно R _AB (см. рисунок). Тогда исходная схема эквивалентна следующей:

Искомое сопротивление 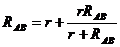, откуда получаем .

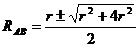Отрицательный корень не имеет физического смысла, поэтому окончательный ответ

.

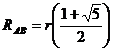8. Пространство между обкладками плоского конденсатора, имеющими форму круглых дисков, заполнено однородной слабо проводящей средой с удельным сопротивлением r и диэлектрической проницаемостью e. Расстояние между обкладками d. Пренебрегая краевыми эффектами, найти напряжённость магнитного поля между обкладками на расстоянии r от их оси, если на конденсатор подано переменное напряжение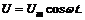

Решение.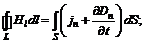

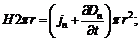
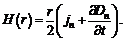
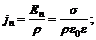
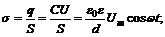
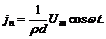
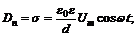
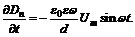
Таким образом, 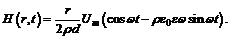Положим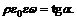

Тогда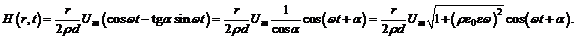

Или 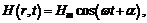где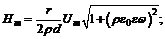

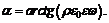
9. Тонкостенная пластмассовая трубка с массой m, длиной ℓ и радиусом r способна вращаться вокруг вертикальной оси, совпадающей со своей продольной осью симметрии. После сообщения трубке угловой скорости ω₀ она приходит во вращение и, вследствие трения в оси, останавливается через промежуток времени t ₁. Чрез какое время t ₂ остановится трубка, если перед сообщением ей скорости ω₀ по её поверхности равномерно распределить заряд q? Трубку считать длинной, так что ℓ >> r.

Решение: В отсутствии заряда величина ускорения вращающейся трубки определяется уравнением движения

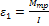(1),

где 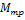– момент сил трения, 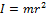– момент инерции трубки.

Трубка с распределенным по ней зарядом q, вращающаяся с угловой скоростью ω, создает круговой ток с силой тока

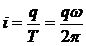(2)

Внутри трубки создаётся магнитное поле, индукция которого зависит от тока, текущего по единице длины (аналогично полю длинного соленоида)

(3)

Изменение угловой скорости при торможении трубки приводит к изменению индукции и, следовательно, к появлению вихревого поля с напряжённостью .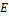

Согласно закону электромагнитной индукции

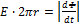(4),

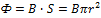где (5).

Из (2),(3),(4),(5) получим

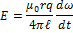
Электрическое поле создаёт момент сил, направленный против силы трения и препятствующий торможению:

(6)

Уравнение движения трубки:

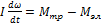(7)

Подставляя (6) в (7), выразим угловое ускорение трубки :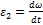

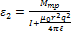(8)

Так как время остановки 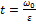, то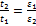

Учитывая (1) и (8),получаем: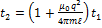

10. На дифракционную решётку длиной 1,5 см с числом щелей 10⁴ падает свет под углом 30^о. Свет содержит дублет спектральных линий с длинами волн 499,975 и 500,025 нм. Вычислите расстояние, на котором находятся изображения этих линий на фотопленке в спектре наибольшего порядка, если оптическая сила линзы, проектирующей свет на фотопленку, равна 2 диоптриям.

Решение: D (общее) = ; ;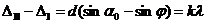

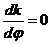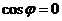, Þ j = ±1. ;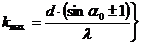

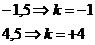| k | =4; 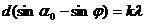; 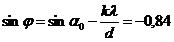, Þ 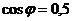; 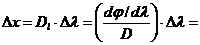1,34×10^-4 м.

11. От двух когерентных источников в данную точку Р попадает свет. Если включить только первый источник, то в точку Р будет попадать 10⁶ фотонов в 1с, если включить только второй, то попадет 4×10⁶ фотонов в 1 с. Какое количество фотонов попадет в точку Р за 1 с от включения обоих источников одновременно, если известно, что это число минимально по сравнению с точками, соседними с точкой Р?

Решение: 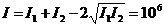с^-1.

Дополнительные задачи:

1. Моль идеального газа с показателем адиабаты g = 1.5 находится в вертикальном цилиндре с теплоизолированными стенками и поршнем. Поршень может перемещаться в цилиндре без трения. На поршень медленно по песчинке насыпают некоторое количество песка так, что давление увеличивается на 3% от исходного значения, после этого весь насыпанный песок резко убирают и дожидаются пока газ придет к равновесию. Насколько в результате таких манипуляций изменится энтропия газа?

Решение: Пусть давление скачком возрастает на D р

a) Найдём, насколько при этом изменится T:

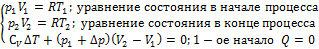
Из первых двух уравнений выразим объёмы и подставим в третье уравнение:

; (*)

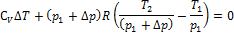
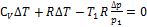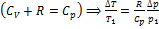б) При сжатии (добавление по песчинке) процесс идет квазиравновесно: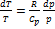

После интегрирования получаем уравнение равновесной адиабаты: .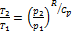

Естественно изменение энтропии при сжатии D S _сжат = 0.

в) При резком возвращении к первоначальному давлению формула (*) дает

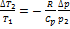(**) (в данном случае ).

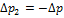Изменение энтропии при таком неравновесном расширении:

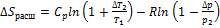, учитывая малость относительных отклонений t и p, раскладывая логарифм в ряд с точностью до квадратичных слагаемых и подставляя (**), получаем: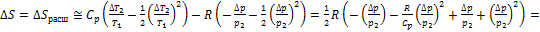

= .

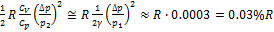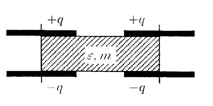
2. Два одинаковых плоских изолированных конденсатора с квадратными обкладками расположены так, как показано на рисунке. В конденсаторы вставлена длинная диэлектрическая пластинка массой m с диэлектрической проницаемостью 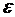. Толщина пластинки равна зазору конденсаторов. В положении равновесия диэлектрик заполняет половину объема каждого из конденсаторов. Ёмкость конденсатора без диэлектрика равна C ₀, сторона обкладки конденсатора l, конденсаторам сообщены одинаковые заряды q.

1) Определить частоту малых горизонтальных колебаний диэлектрической пластинки, пренебрегая силами трения.

2) Какие колебания будет совершать пластинка, если конденсаторы соединить параллельно?

.

Решение. Обозначим смещение пластинки из положения равновесия через x. Рассматривая каждый конденсатор как параллельное соединение конденсатора с диэлектриком и воздушного, для их ёмкостей получим:

; .

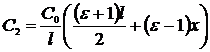Энергия системы двух конденсаторов равна

.

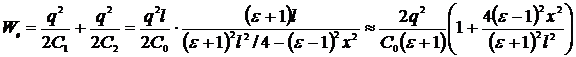Полная энергия системы конденсаторы-пластинка сохраняется:

.

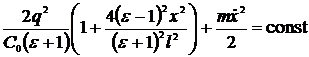Дифференцируя это выражение по времени и учитывая, что 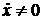, получаем уравнение гармонического осциллятора:

.

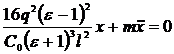Следовательно, частота колебаний пластинки равна .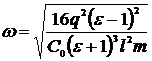

2) Если конденсаторы соединены параллельно, их полная энергия 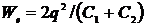не зависит от x, следовательно, пластинка колебаться не будет.

3. Существуют различные конструкции черенковских счётчиков, в которых излучение Вавилова-Черенкова используется для регистрации быстро двигающихся заряженных частиц. Частицы попадают на блок ABCD прозрачного вещества и возбуждают в нем черенковское излучение. Излучение выходит через грань AB и попадает на фотоумножитель. Считая, что частицы двигаются по нормали к грани CD, как на рисунке, определите, при каких скоростях они могут регистрироваться счётчиком, если показатель преломления вещества блока равен n. При каком показателе преломления n ультрарелятивистские (β = V /c≤ 1) частицы не могут регистрироваться?

Ответ: черенковское излучение возникает при следующем условии: 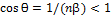. Чтобы это излучение могло выйти через грань AB, на границе раздела не должно наблюдаться полного внутреннего отражения, т.е. 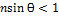,иначе 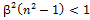. При этих условиях частицы будут регистрироваться при скоростях, удовлетворяющих неравенству 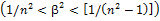. Для регистрации частиц (β ≈ 1) это условие не выполняется при 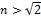(частицы не регистрируются).

4. Вблизи спектральной линии обычного водорода с длиной волны l₁ = 486,1320 нм
Г.К. Юри в 1931 г. обнаружил линию с длиной волны l₂ = 485,9975 нм. Предполагая, что эта спектральная линия обусловлена примесью одного из более тяжёлых изотопов водорода, определите во сколько раз атомная масса этого изотопа больше, чем атомная масса обычного водорода.

Решение. По Бору .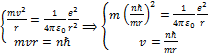

Отсюда .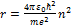

.

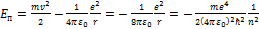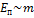, здесь 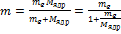– приведённая масса электрона в атоме.

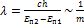для длины волны перехода между заданными уровнями .

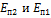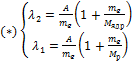, где 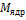– масса ядра изотопа, 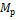– масса протона, A – некоторая комбинация постоянных, одинаковая для исследуемого изотопа и атома обычного водорода (протия).

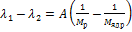Поделим это уравнение на второе уравнение системы (*)
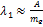– в первом порядке малости.

,

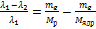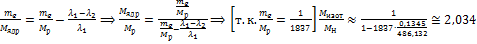
. Изотоп – дейтерий.