Симметрия в мире растений

Те общие соображения о симметрии, которые были изложены в главе о животных, применимы, разумеется, и к растительным организмам. От животных растения отличаются вообще своей неподвижностью и в соответствии с этим меньшей пластичностью своих тканей. Поэтому мы вправе ожидать, что в растениях мы встретим более благоприятные условия для проявления симметрии. Наблюдение, действительно, широко подтверждает такое предположение. Как в животных, так и в растениях природа постоянно осуществляет принцип экономии. В растении мы видим также, как целый организм составляется из однообразного повторения одинаковых и одинаково расположенных друг относительно друга частей.

Однако между симметрией животных и растений есть громадная разница. Если для жизни животных в большинстве случаев свести внешнюю поверхность тела до возможно меньшего размера, для растений это является совершенно невозможным. Растение устроено так, что должно питаться исключительно внешнею своею поверхностью: с этой внешней поверхностью соприкасаются, с одной стороны, воздух, составные части которого усваиваются листьями, с другой – минеральные составные части почвы, усваиваемые корнями. Так как такое усвоение производится поверхностью растения, то эта поверхность должна иметь большую площадь. Она обыкновенно разбивается на множество отдельных частей, - листьев и корней. Помимо этой существенной разницы, симметрия растений, как и животных, сводится на симметрию его органов и на симметрию взаимного расположения этих органов. Как и у неподвижных животных, у растений преобладает лучевая форма симметрии.

Типичным примером лучистой симметрии может служить круглый ствол наших двудольных деревьев с его годичными концентрическими кольцами и радиальными лучами. Не у всех растений, однако, ствол или стебель бывает круглый: иногда он бывает четырёхгранным или трёхгранным.

Листья по своему физиологическому назначению должны обладать большой поверхностью, так как они служат для усвоения углекислоты из воздуха, для дыхания и испарения. Поэтому наиболее совершенная форма листа должна быть пластинчатая, а так как лист одним концом прикреплён к стеблю, то его пластинка естественно должна обладать двусторонней симметрией. Эта симметрия иногда не выдерживается строго, и по одну сторону своего срединного нерва лист бывает больше, чем по другую. Но и в листе часто остаются следы лучевой симметрии: вспомним почти круглый лист настурции с прикреплённым почти в середине его черешком, соединенным с листом почти перпендикулярно; вспомним разрезной лист конского каштана, лапчатый лист клёна.

Части цветка произошли из видоизмененных листьев, поэтому некоторые из этих частей сохраняют пластинчатую форму, а иногда и двустороннюю симметрию листа, как лепестки и чашелистики. В цветах растений природа, несомненно, воплотила идею красоты, а поэтому интересно будет остановиться на симметрии именно этих органов растений.

Совершенно несимметричные цветы встречаются у растений очень редко, обыкновенно же они бывают с одной плоскостью симметрии, так называемые зигоморфные (рис.72 слева), и с несколькими плоскостями симметрии – актиноморфные цветы(рис.72 справа и рис. 73).

Примером зигоморфного цветка может служить цветок какого-нибудь мотылькового растения, например, гороха, или цветок Иван-чая (Epilóbium angustifolium,рис. 72 слева).

Чрезвычайно интересно, что двусторонняя симметрия цветка часто бывает внешнего происхождения, а именно, она образуется под влиянием силы тяжести. Это доказывается следующим простым опытом. На время цветения растение прикрепляется к особому аппарату – клиностату, снабженному часовым механизмом, с помощью которого растения можно вращать в определённом направлении. Если вращать растение так, чтобы верхушка его то опускалась, то поднималась, то сила тяжести будет во всё время вращения действовать на растение по различным направлениям, и совершенно утратится её характерное постоянное действие в одном направлении – сверху вниз. Оказывается, что распустившиеся в таких условиях зигоморфные цветы становятся лучевыми, актиноморфными. На рис. 72 справа изображён цветок Иван- чая, превращенный вышеописанными способами в актиноморфный.

Симметрия актиноморфных цветов бывает тройная, четверная и пятерная. Она, очевидно, имеет тесную связь с внутренней природой растения, так как у однодольных растений мы наблюдаем обыкновенно тройную симметрию цветка, а у двудольных же пятерную и иногда четверную. У однодольных тройная симметрия так распространена, что однодольное растение вороний глаз, Pāris quadrifōlia (рис. 74), с четверной симметрией составляет интересное исключение. У этого растения четверная симметрия распространяется и на расположение листьев и на цветок.

Симметрия цветка распространяется также и на плод, составные части которого в молодости составляют лишь часть цветка. Припомним яблоко или грушу с их радикальной симметрией и стручок гороха с двусторонней.

Все перечисленные случаи симметрии частей растений общеизвестны, и останавливаться на них подробнее нет надобности. Но в высшей степени замечательно и имеет глубокий философский смысл то проявление симметрии в растениях, которое выражается в периодическом повторении одинаковых частей растения по его длине. Мы видели выше, когда говорили о симметрии вообще, что прямолинейная последовательность одинаковых равностоящих предметов есть особый вид симметрии. Для полноты симметрии, однако, необходимо, чтобы такой ряд был бесконечен. Если мы возьмём какое-нибудь высшее растение, положим, дерево, то увидим что оно растёт периодически, увеличиваясь каждый год на определённую длину. Теоретически тут мы имеем дело с беспредельным периодическим повторением одного и того же процесса роста, который в действительности не беспределен только благодаря различным противодействиям, в виде силы тяжести, в виде постепенного истощения жизненной энергии организма и необходимости возобновления последней путём полового размножения и проч. Каждое новое растение, вырастающее из семян старого, представляет, в свою очередь, лишь один из периодов в росте бесконечной непрерывной цепи происходящих друг от друга неделимых. Таким образом, мы видим, что тот род симметрии, который характеризуется элементом поступательного перемещения, широко осуществляется в растениях, насколько это позволяет природа растительного организма и внешние условия его существования на земле.

Эта симметрия поступания выражается в высшей степени рельефно в так называемом листорасположении. Под этим термином надо понимать не только расположение листьев на стебле и ветвях, но и расположение вообще органов, происшедших из листьев – частей цветка, чешуек в почке, в еловой шишке и т.п.

Закон, по которому расположены листовые органы на побеге, можно определить следующим образом. Срежем побег перпендикулярно к его длине, на уровне одного листа. Затем от основания этого листа проведём по поверхности побега кратчайшую линию к основанию листа, ближайшего к первому и к линии среза. Самый побег при этом мы вообразим себе в виде правильного круглого цилиндра. Чтобы перейти от первого листа ко второму, надо по круговой линии среза пройти некоторый путь, т.е. повернуть цилиндр на некоторый угол, так называемый угол расхождения листьев, и затем пройти по образующей цилиндра, т.е. по длине побега, некоторое расстояние. Таким образом, мы имеем характерные для винтовой оси поворот и поступательное перемещение. Заметим, что ботаник называют образующую цилиндра, проходящую через основание листа, ортостихой. Переходя по винту к следующему листу, мы опять должны сделать поворот на прежний угол расхождения и пройти по следующей ортостихе прежнее расстояние. Угол расхождения может быть целою частью не одного, а нескольких полных поворотов. Так, например, угол расхождения может быть равен окружности. Это значит, что цилиндр надо повернуть пять раз на оси для перехода от листа к листу, при чём за это время цилиндр совершит два полных оборота и придёт в прежнее положение, при котором по винтовой линии мы дойдём до листа, помещающего выше первого на одной с ним ортостихе. Мы прошли от листа к листу по так называемой основной, или генетической, спирали, прошли по двум её полным оборотам и встретили по пути пять листьев, составляющих листовой цикл. Поэтому в данном случае угол расхождения, характеризующий листовой цикл, обозначается дробью . В знаменателе этой дроби стоит число листьев цикла, а в числителе – число полных оборотов спирали.

На рис. 75 изображены два случая листорасположения, выражающиеся дробями и . Рис 76. Представляет листорасположение клёна, для которого надо принять две

генетические спирали, идущие от двух взаимно противоположных листьев; для каждой спирали листоположение выразится дробью .

Для изображения листового цикла служат диаграммы, на которых цилиндр заменяется конусом, а самый конус изображается так, как если бы мы на него смотрели сверху вниз, - основание его нам представляется кругом, а вершина совпадает с центром этого круга; ортостихи заменяются образующими конуса и изобразятся радиусами круга. Винтовая линия изобразится спиралью, огибающею центр круга и оканчивающийся в этом центре. На рис. 77-80 представлены такие диаграммы для случаев листорасположения , и . Самые распространенные случаи изображаются дробями , , , и . Дроби эти имеют замечательное свойство: сумма числителей двух смежных дробей даёт числителя, сумма знаменателей – знаменателя дроби, следующей за двумя взятыми дробями.

Можно считать листья по побегу и в обратную сторону. Тогда мв получим то же число листьев цикла, но число оборотов спирали будет иное, а именно оно будет равно дополнению числителя до знаменателя. Напр., если, считая в одном направлении, мы получим дробь , то в другом получим 1 – = .

Переходя от листа к листу по генетической спирали, мы часто минуем лист, наиболее близкий у первоначальному, потому что он отстоит дальше от основания побега, чем лист на генетической спирали, а между тем этот переход от листа к листу в ближайшем направлении иногда очень бросается в глаза. Это видно, напр., на еловой шишке (рис. 81), где чешуйки, ближайшие друг к другу, так и хочется соединить спиралью и притом как вправо, так и влево. Эти бросающиеся в глаза винтовые линии называются у ботаников парастихами. Если назвать парастихой вообще каждую винтовую линию, проходящую через основания двух произвольно выбранных листьев, то в этом смысле и генетическая спираль, и ортостиха будут парастихами, выделяющимися, однакоже, из общего числа парастих своим специальным значением. Так как обе вышеупомянутые парастихами, соединящие наиболее близкие друг к другу листовые органы, особенно выделяются из общего числа парастих, то мы назовём их главными парасихами. Полезно ещё различать одну линию – линию горизонтального среза, не витую, разомкнутую, а кольцевую, замкнутую, проходящую только через один начальный нижний лист и представляющуб окружность основания цилиндрического побега. Эту линию можно было бы назвать гипостихой; она представляет лишь частный случай парастих.

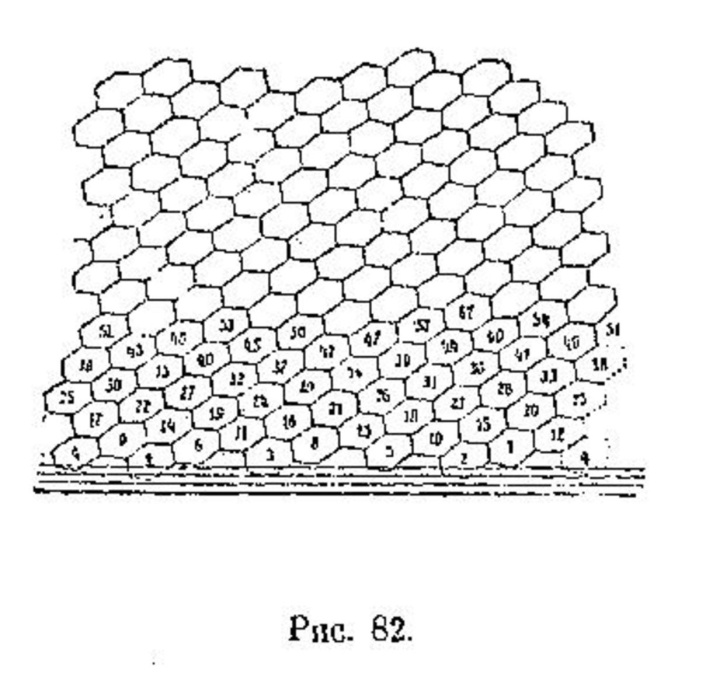
Следует заметить, что на одной парастихе расположены не только те два листа, через которые она проведена, но целый ряд листьев. Если пронумеровать листья вдоль генетической спирали, то окажется что номера листьев, расположенных на одной парастихе, разнятся между собой на какое-нибудь постоянное число, напр.: 0,5,10,15 и т.д., или: 3.11,19.27 и т.д, при чём эта разница одинакова у парастих одного направления, параллельных друг другу, и притом равна числу парастих, которое можно сосчитать, обходя вокруг побега поперёк: если при таком обходе мы сосчитаем пять парастих одного наклона, то номера листовых органов, расположенных на каждой из таких парастих будут отличаться друг от друга на 5, и т.д. Этим свойством парастих легко воспользоваться, чтобы перенумеровать листы на побеге. На рис.82 представлена еловая шишка, развёрнутая на плоскости, при чём схематически чешуйки шишки обозначены шестиугольниками. На шишке бросаются в глаза два ряда главных парастих, подымающихся справа налево, -восемь, число менее крутых и подымающее слева направо – пять. Среди шестиугольников легко проследить эти два ряда парастих и следую этим парстихам, легко пронумеровать шестиугольники, приняв один из шестиугольников за номер первый.

Заметим ещё, что, взяв отношение чисел, характерных для обеих главных парастих, мы получим дробь, входящую в ряды дробей данного листорасположения. Напр., для данной шишки эта дробь будет 5/8, входящая в ряды 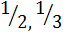, , …, так как = 1 - . Приняв, что над первым номером как раз выше лежит номер 22, мы установим для нашей шишки листорасположение ; если сочтём, что ещё ближе к вертикали номер 35, то листорасположение будет .

Интересно ближе рассмотреть свойства чисел, характеризующих данное расположение. Напишем ряд дробей

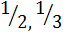, , , , , , и т.д.

Выразив эти обыкновенные дроби десятичными, получим, с точностью до четвертого знака:

0,5000; 0,3333; 0,4000; 0,3750; 0,3846; 0,3809; 0,3823; 0,3818; 0,3820.

Мы видим, что эти дроби постепенно становятся всё ближе друг к другу. Конечно, если бы мы вычислили наши десятичные дроби с большим числом знаков, мы бы и в последних их взятых дробей нашли более заметную разницу, и для того. Чтобы её сгладить, надо было бы взять дроби, ещё более отдалённые от начала нашего ряда. Как бы мы далеко от начала ни взяли две смежные дроби, вычисляя достаточное число десятичных знаков, мы всегда найдём разницу, но эта разница будет становится всё меньше и меньше. Возьмём вместо наших дробей число ; то число не может быть определено точно, так как корень квадратный из пяти есть число иррациональное, для выражения своего требующее бесконечного числа десятичных знаков. Первые восемь десятичных знака числа будут 0,38196601. Вычисляя как угодно точно, т.е. с каким угодно числом десятичных знаков, наши дроби и число мы найдем, что чем дальше от начала брать дробь, тем с большей точностью она будет воспроизводить это число, т.е. тем меньше будет разница между дробью и нашим числом. Говорят, что иррациональные число есть предел дробей нашего ряда. Оно является вместе с тем истинным выражением для взятого листорасположения. Мы пришли к неожиданному результату, что листорасположение выражается только на первый взгляд рациональными дробями, т.е. дробями, числитель и знаменатель которых - целые числа, на самом же деле оно выражается иррациональным числом. Для других случаев листорасположения мы найдём и другие иррациональные числа, подобные вышеуказанному. Рациональные дроби представляют только приблизительные значения настоящей предельной величины, характеризующей листорасположение. Мы укажем ещё на происхождение этих приблизительных величин.

Число , как этому учит алгебра, представляет значение так называемой непрерывной дроби,

продолжающейся без конца.

Действительно, вычисляя последовательно дроби

= , = ,

и т.д., мы придём последовательно к каждой из обыкновенных дробей нашего ряда. Поэтому эти дроби называются подходящими дробями взятой непрерывной дроби. Они поочередно то больше, то меньше предельного значения всей непрерывной дроби.

Нельзя не отметить ещё одного удивительного свойства чисел, характеризующих наиболее часто встречающиеся виды листорасположения, т.е. ряда дробей 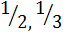, , и т.д. Мы видели, что предельное значение этих дробей есть . Оказывается, что если разделить длину, равную единице, на такие две части, чтобы вся длина относилась к большей части, как большая часть к меньшей, то большая часть будет , а меньшая Деление прямого отрезка на такие части называется золотым делением. Ему придают большое эстетическое значение и находят его во взаимном соотношении частей предметов, производящих на нас впечатление красоты, будут ли это творения природы, как, напр., красивое человеческое тело, или же произведение искусства, как напр., красивое здание.

Таков в общих чертах замечательный закон листорасположения. Мы потому подробнее остановились на нём, что он представляет самое блестящее приложение понятия о симметрии к учению о формах организмов. Мы ещё вернёмся к этому закону, когда будем говорить об аналогии между ним и законом кратных отношений в кристаллах.

Располагаясь винтом по побегу, листья ка бы раскидываются во все стороны и не заслоняют друг друга от света, столь необходимого

для жизни растений. Смотря на побег сверху, мы видим листорасположение в так называемой мозаике листьев (рис.83).