Обобщенная Многокомпонентная оптимальная интерполяция
Если определить объединяющий вектор для двух переменных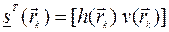 
, тогда вектор размерности 
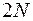в точках наблюдений может быть определен как
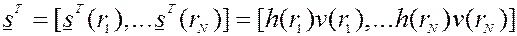
Тогда система уравнений корректировки (анализа) может быть сведена к системе
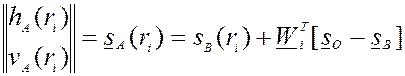
Где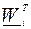 
вектор апостериорных весов с элементами – подматрицами 
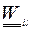, размерности 
.
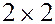Уравнение для определения весов также может быть записано в форме, совпадающей с уравнением для одной переменной:
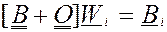
Где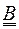 
и 
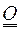квадратные ковариационные матрицы с элементами-подматрицам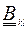и 
и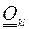 
, соответственно. А 
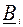- вектор с элементами-подматрицами 
.
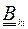Если количество переменных увеличивается, то, опять же, система уравнений сохраняет свой вид, то размерность вектора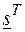 
увеличивается до 3N, 4N и т.д. Соответственно увеличивается и размерность матриц в системе уравнений для определения весов.
Также может быть получена нормализованная (безразмерная) форма алгоритма оптимальной интерполяции для нескольких переменных. Если нет наблюдени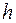й 
или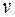 
на какой-то конкретной станции, то порядок матриц 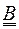и 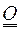сокращается на единицу. Если ошибки наблюдений пространственно не коррелируют и нет корреляций измерений между разными переменными, то все элементы 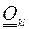, за исключением диагональных обращаются в ноль, а все элементы 
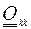тоже обращаются в нуль за исключением 
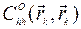и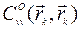 
.
Данный алгоритм, также как и алгоритм для одной переменной, может быть записан в форме с исключенными весами. Так для произвольного узла модельной сетки с радиусом вектором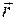 
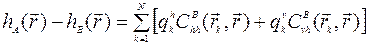
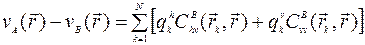
Где
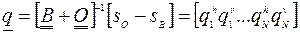
Ограничения метода оптимальной интерполяции
1. Проблема интерполяции. Предполагается, что фоновые оценки известны как в узлах модельной сетки, так и в точках наблюдений. Если в качестве фоновых оценок используется моделирование, то в качестве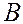 
мы имеем результаты модельного расчета в узлах модельной сетки. Для того чтобы получить 
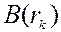в точках измерений необходимо интерполировать модельные значения из узлов модельной сетки в точки измерений. Это прямая задача и она может быть источником дополнительных ошибок. Особенно это существенно для интерполяции по вертикали, т.к. изменчивость процессов по высоте значительно больше, чем в горизонтальном направлении.
2. Корреляция ошибок измерений и оценок первого приближения. В алгоритме оптимальной интерполяции существенным допущением является предположение о некоррелируемости ошибок измерений и результатов моделирования. Если используются спутниковые измерения, то часто такая связь существует, т.к. измеряются радиационные характеристики, а по ним восстанавливаются профили температуры, ветра и т.д. При этом может использоваться информация о норме, т.е. о фоновых оценках по результатам моделирования, т.е. ошибки могут корредировать.
3. Упрощение матрицы ковариаций оценки первого приближения. В реальной практике часто используются предположения об однородности, изотропности, независимости ковариаций по разным пространственным направлениям. Это может привести к дополнительным ошибкам.
4. Оценка матрицы ковариаций оценки нормы в местах отсутствия измерений. Если измерительная сеть густая, то измерения регулярно используются для оценки матрицы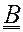 
. Если станций мало, то оценка 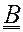в сильной степени зависит от точности используемой модели и возраста последнего измерения. Если измерений долго не было, то в качестве фоновых оценок используются климатические значения.
5. Непрерывность корреляционных функций. Для производных используются конечно-разностные представления, нпр.:
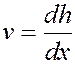
фактически заменяется на
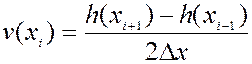
где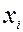 
представляют собой модельную сетку. Для многих соотношений оценок ковариаций используется условие непрерывности изменчивости ковариационных функций и использование дискретных значений для производных приводит к погрешностям.
6. Локализация использования алгоритма. Обычно алгоритм оптимальной интерполяции используется локально. Это означает, что средняя ошибка по всей модельной сетке не обязательно достигает минимума.