Занятия 1, 2. Комплексные числа и действия над ними
Комплексными числами называются объекты вида 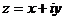 , где
, где 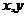 – действительные числа, для которых
– действительные числа, для которых
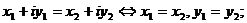

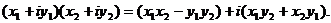
Комплексные числа складываются, вычитаются и умножаются по законам обычной алгебры с учетом того, что 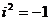 . Символ
. Символ 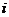 называется мнимой единицей.
называется мнимой единицей.
Приняты следующие обозначения:
 – множество всех комплексных чисел;
– множество всех комплексных чисел;
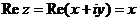 – действительная часть числа
– действительная часть числа  ;
;
 – мнимая часть числа
– мнимая часть числа  ;
;
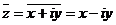 – число, сопряженное с числом
– число, сопряженное с числом  .
.
Геометрически число 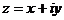 изображается как точка
изображается как точка 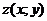 на координатной плоскости Oxy или как вектор
на координатной плоскости Oxy или как вектор 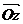 (рис.1).
(рис.1).
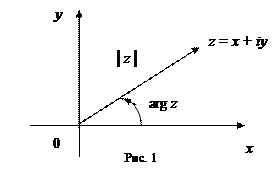
Длина вектора 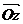 называется модулем комплексного числа
называется модулем комплексного числа  и обозначается
и обозначается 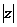 . Модуль числа
. Модуль числа  определяется формулой
определяется формулой

и обладает всеми свойствами модуля действительного числа.
Любой угол между осью  и вектором
и вектором 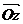 называется аргументом числа
называется аргументом числа  и обозначается
и обозначается  , а угол из промежутка
, а угол из промежутка  называется главным значением аргумента и обозначается
называется главным значением аргумента и обозначается 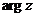 .
.
Функции 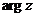 и
и  для
для 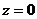 не определены.
не определены.
В зависимости от того, в какой четверти расположено число 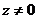 (рис. 2), главное значение
(рис. 2), главное значение 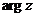 определяется однозначно формулой
определяется однозначно формулой
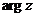 =
= 
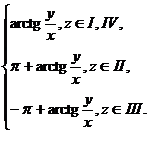
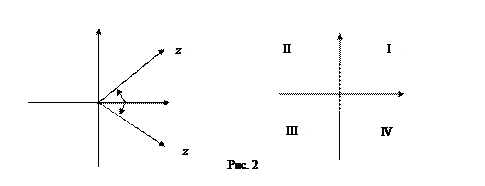
 в отличие от
в отличие от 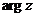 для каждого
для каждого 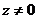 принимает бесконечно много значений, т. е. представляет собой бесконечное множество действительных чисел
принимает бесконечно много значений, т. е. представляет собой бесконечное множество действительных чисел
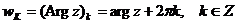 .
.
Ради удобства пишут:
 =
=  .
.
В зависимости от решаемой задачи применяются различные формы записи комплексного числа.
Алгебраическая форма: 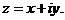
Показательная форма: 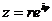 ,
,
где 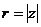 и
и  - одно из значений
- одно из значений  . Можно взять, например,
. Можно взять, например,  . Функция
. Функция 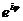 обладает всеми свойствами показательной функции.
обладает всеми свойствами показательной функции.
Тригонометрическая форма:
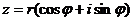 ,
,
где 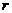 и
и  имеют тот же смысл, что и в показательной форме.
имеют тот же смысл, что и в показательной форме.
Переход от показательной формы к тригонометрической и обратный переход осуществляются на основе формулы Эйлера:
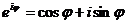 .
.
Следует учесть, что при сложении и вычитании комплексных чисел удобно пользоваться алгебраической формой, а при умножении, делении и, особенно, при возведении в большие степени удобно пользоваться показательной формой.
Если  ,то
,то
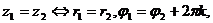
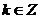 ,
,
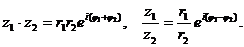
Если 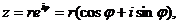 то
то 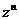 и
и 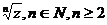 определяются по формулам Муавра:
определяются по формулам Муавра:
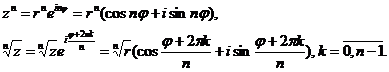 Функция
Функция  для каждого значения
для каждого значения  принимает
принимает 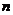 различных значений, т.е. представляет собой множество из
различных значений, т.е. представляет собой множество из 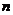 различных комплексных чисел
различных комплексных чисел

Множество 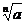 ,
, 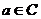 есть множество решений уравнений
есть множество решений уравнений
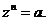
Множество решений квадратного уравнения
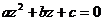
с комплексными коэффициентами  дается формулой
дается формулой
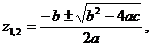
где под 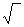 понимается одно из значений квадратного корня из комплексного числа.
понимается одно из значений квадратного корня из комплексного числа.
Теоретические упражнения
1. Пользуясь определением модуля, доказать, что модуль комплексного числа удовлетворяет неравенствам треугольника:
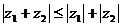 ;
; 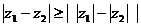
2. Доказать, что операции сложения и умножения комплексных чисел обладают свойствами:
а) коммутативности:
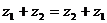 ,
, 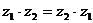 ;
;
б) ассоциативности:
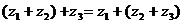 ,
, 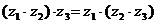 ;
;
в) дистрибутивности умножения относительно сложения:
 .
.
3. Доказать следующие свойства сопряженных комплексных чисел:
а) 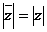 ;
; 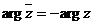 ; б)
; б) 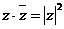 ;
;
в) 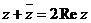 ;
;  .
.
4. Основываясь на результатах предыдущей задачи вывести формулы для действительной и мнимой частей комплексного числа 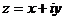 :
:
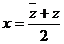 ;
; 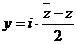 .
.
Задачи
1. Найти 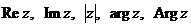 следующих комплексных чисел:
следующих комплексных чисел:
а) 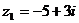 , ,
| д) 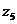 = 8, = 8,
|
б) 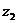 = = 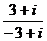 , ,
| е)  = -3, = -3,
|
в) 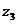 = = 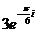 , ,
| ж) 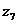 = =  . .
|
г) 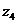 = = 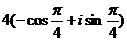 , ,
|
Решение:
а) 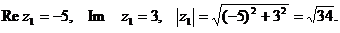
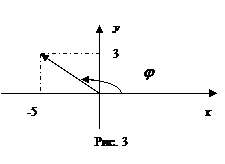
Изобразим число 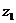 на комплексной плоскости (см. рис.1). Из рис. 3 видим, что угол
на комплексной плоскости (см. рис.1). Из рис. 3 видим, что угол  между осью
между осью  и вектором
и вектором 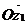 , принадлежащий промежутку
, принадлежащий промежутку 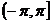 , будет равен
, будет равен 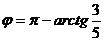 .
.
Значит, 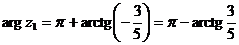 ,
,

б) Умножим числитель и знаменатель числа 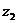 на сопряженное к знаменателю, т. е. на
на сопряженное к знаменателю, т. е. на 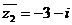 , получим:
, получим:
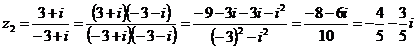
Тогда
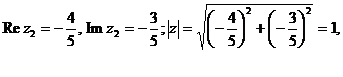
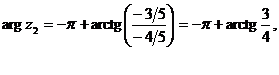

в) Сравнивая число 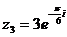 с показательной формой
с показательной формой 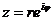 комплексного числа, видим, что 3 есть
комплексного числа, видим, что 3 есть  , а
, а 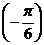 одно из значений аргумента. Так как
одно из значений аргумента. Так как 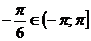 , то
, то
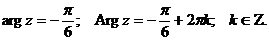
Согласно формуле Эйлера

Значит,
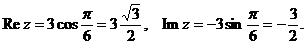
г) 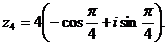
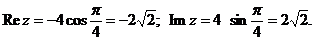
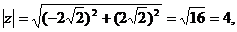
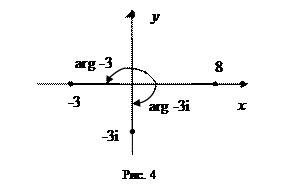
 д), е), ж)
д), е), ж) 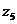 = 8,
= 8,  =
= 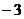 ,
, 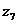 =
=  .
.
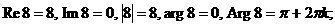
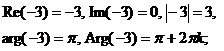
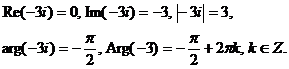
2. Записать следующие комплексные числа в показательной и тригонометрической формах:
а) 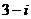 , б)
, б)  , в)
, в)  , г)
, г) 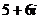 .
.
Решение:
а) так как 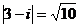 ,
, 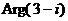 =
=  , то взяв
, то взяв 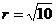 и одно из значений аргумента
и одно из значений аргумента 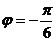 , получим число
, получим число 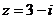 в показательной форме:
в показательной форме:  . Применяя формулу Эйлера, получим
. Применяя формулу Эйлера, получим  Значит, тригонометрическая форма
Значит, тригонометрическая форма 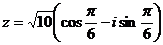 ;
;
б) Так как 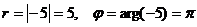 - одно из значений аргумента, то
- одно из значений аргумента, то
 ;
;
в) Так как 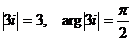 , то
, то

г) Так как 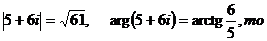
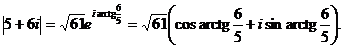
3. Вычислить 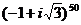 .
.
Решение.Запишем число  в показательной форме. Так как
в показательной форме. Так как 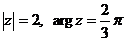 (см. рис.5), то
(см. рис.5), то
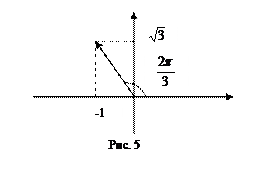
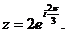 Тогда по формуле Муавра
Тогда по формуле Муавра
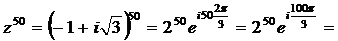
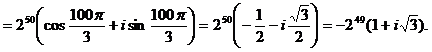
4. Найти все значения следующих корней:
а)  , б)
, б) 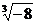 .
.
Решение:
а) Представим число 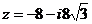 в тригонометрической форме. Для этого вычислим
в тригонометрической форме. Для этого вычислим 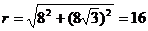 ,
, 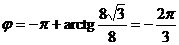 . Тогда
. Тогда
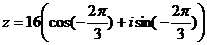 .
.
По формуле Муавра получаем
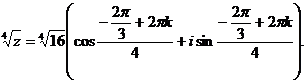
При различных  получим следующие значения корня:
получим следующие значения корня:

б) Так как число 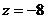 в тригонометрической форме имеет запись
в тригонометрической форме имеет запись  , то по формуле Муавра
, то по формуле Муавра
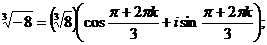
при 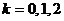 получим
получим 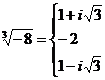 .
.
5. Решить уравнения:
а) 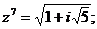 б)
б) 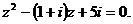
Решение:
а) Множество решений уравнения 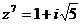 совпадает с множеством всевозможных различных значений
совпадает с множеством всевозможных различных значений 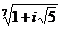 .Так как
.Так как 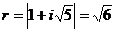 ,
, 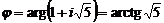 , то по формуле Муавра
, то по формуле Муавра
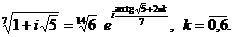
Следовательно, корнями уравнения будут числа:
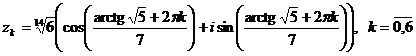
б) По формуле корней квадратного уравнения
 ,
,
где под 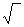 понимается одно из значений квадратного корня. Так как
понимается одно из значений квадратного корня. Так как 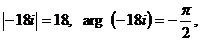 то
то 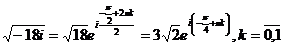 .
.
При 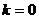 получаем одно из значений квадратного корня
получаем одно из значений квадратного корня
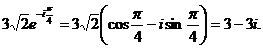
Значит,  , т.е. уравнение имеет корни
, т.е. уравнение имеет корни
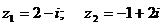 .
.
6. Изобразить на комплексной плоскости множество точек  , заданное условиями
, заданное условиями
а)  , в)
, в)  ,
,
б) 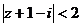 , г)
, г) 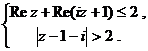
Решение:
а) Модуль  есть расстояние между точками
есть расстояние между точками  и
и 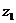 . Следовательно, соотношению
. Следовательно, соотношению  удовлетворяют те и только те точки
удовлетворяют те и только те точки  комплексной плоскости, которые равноудалены от точек
комплексной плоскости, которые равноудалены от точек 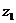 и
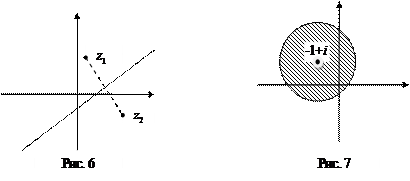
и 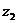 . Как известно, множество таких точек есть серединный перпендикуляр к отрезку с концами в точках
. Как известно, множество таких точек есть серединный перпендикуляр к отрезку с концами в точках 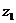 и
и 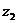 (рис.6).
(рис.6).
б) Неравенству 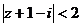 удовлетворяют те и только те точки
удовлетворяют те и только те точки  комплексной плоскости, расстояние от которых до точки
комплексной плоскости, расстояние от которых до точки 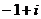 меньше 2. Множество таких точек есть внутренность круга радиуса 2 с центром в точке
меньше 2. Множество таких точек есть внутренность круга радиуса 2 с центром в точке 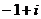 (рис.7).
(рис.7).
в) Неравенствам  удовлетворяют те и только те точки
удовлетворяют те и только те точки  , для которых угол между осью
, для которых угол между осью  и вектором, имеющим начало в точке
и вектором, имеющим начало в точке 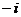 и конец в точке
и конец в точке  , больше
, больше  и меньше
и меньше  , включая
, включая  . Это есть угол с вершиной в точке
. Это есть угол с вершиной в точке 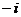 , за исключением одной стороны (рис. 8).
, за исключением одной стороны (рис. 8).
г) Так как  , а
, а
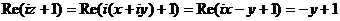 ,
,
то первое неравенство имеет вид 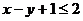 , откуда
, откуда 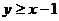 . Этому неравенству удовлетворяют те и только те точки
. Этому неравенству удовлетворяют те и только те точки  , которые лежат в полуплоскости, выше прямой
, которые лежат в полуплоскости, выше прямой 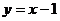 , включая саму прямую. Второе неравенство определяет внешность окружности радиуса 2 с центром в точке
, включая саму прямую. Второе неравенство определяет внешность окружности радиуса 2 с центром в точке 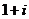 . Значит, решением системы будет внешность этой окружности, расположенная выше прямой
. Значит, решением системы будет внешность этой окружности, расположенная выше прямой 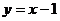 (рис.9).
(рис.9).
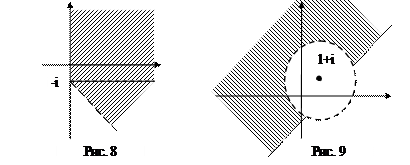
Задачи для самостоятельного решения
1. Найти 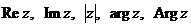 следующих комплексных чисел:
следующих комплексных чисел:
а)  ; ;
| б)  = =  ; ;
|
в)  = = 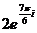 ; ;
| г)  = = 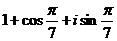 . .
|
2. Записать следующие комплексные числа в показательной и тригонометрической формах:
а) 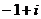 ; б)
; б) 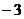 ; в)
; в) 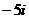 ; г)
; г) 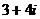 .
.
3. Вычислить:
а)  ; в)
; в) 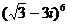 ;
;
б) 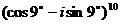 ; г)
; г) 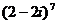 .
.
4. Найти все значения следующих корней:
а) 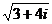 , б)
, б) 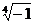 ; в)
; в) 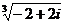 ; г)
; г) 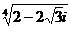 .
.
5. Решить уравнения:
а) 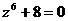 ; б)
; б) 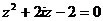 ; в)
; в) 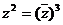 .
.
6. Изобразить на комплексной плоскости множество точек  , заданное условиями
, заданное условиями
а) 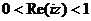 , б)
, б)  ,
,
в)  , г)
, г) 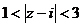 .
.
Ответы и указания
1. а) 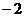 ,
, 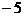 ,
, 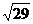 ,
,  ,
, 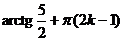 ,
, 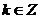 ;
;
б) 0, 1, 1,  ,
, 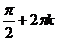 ,
, 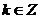 ;
;
в) 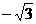 ,
, 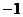 ,
, 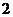 ,
, 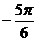 ,
, 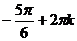 ,
, 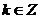 ;
;
г) 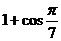 ,
, 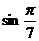 ,
, 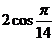 ,
, 
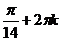 ,
, 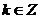 .
.
2. а) 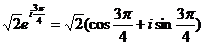 ;
;
б) 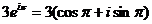 ;
;
в) 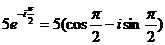 ;
;
г)  .
.
3. а) 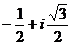 ; б)
; б) 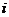 ; в) 1728; г)
; в) 1728; г)  .
.
4. а) 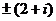 . Обозначить корень через
. Обозначить корень через 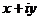 . Тогда
. Тогда 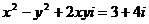 . Откуда найти
. Откуда найти  и
и 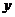 ;
;
б)  ;
; 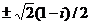 ;
;
в) 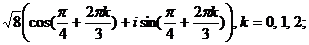
г) 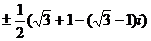 ;
;  .
.
5. а) Решениями уравнения будут все значения 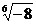 :
:  ;
; 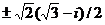 ;
; 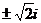 ;
;
б) 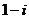 ;
; 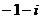 ;
;
в) 0; 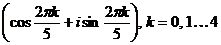 .
.
6. а) полоса 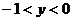 ;
;
б) парабола 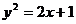 ;
;
в) угол с вершиной в точке 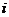 , стороны которого образуют с осью
, стороны которого образуют с осью  соответственно углы
соответственно углы 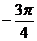 и
и  ;
;
г) кольцо, ограниченное окружностями с центрами в точке 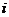 и радиусами 1 и 3 соответственно.
и радиусами 1 и 3 соответственно.