1. Представить в алгебраической форме:
а)  ; б)
; б) 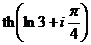 ; в)
; в) 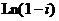 ; г)
; г)  .
.
2. Доказать:
а) 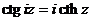 ; б)
; б) 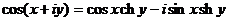 .
.
3. Установить, когда выполняется равенство
 .
.
4. Решить уравнения: а) 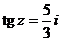 ; б)
; б) 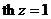 .
.
5. Изобразить кривые, заданные следующими уравнениями и указать их направления:
а)  ;
;
б)  ;
;
в) 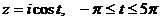 ;
;
г)  ;
;
д) 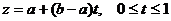 ;
;
е) 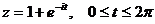 .
.
6. Доказать, что кривая, заданная уравнением
 ,
,
является гладкой.
7. Описать область 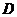 , если ее граница определена параметрически уравнением:
, если ее граница определена параметрически уравнением:
а)  ; б)
; б)  .
.
Ответы и указания
1. а) 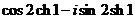 ; б)
; б)  ;
;
в) 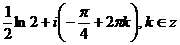 ; г)
; г) 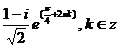 .
.
3. Равенство выполняется, если  , т.е. когда
, т.е. когда 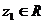 или
или 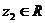 ;
;
4. а)  ; б) корней нет.
; б) корней нет.
5. а) Окружность радиуса  с центром в точке
с центром в точке  , ориентированная против часовой стрелки;
, ориентированная против часовой стрелки;
б) ветвь гиперболы 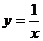 , расположенная в третьем квадранте и направленная слева направо;
, расположенная в третьем квадранте и направленная слева направо;
в) отрезок с концами в точках 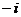 и
и 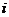 , проходящий четырежды;
, проходящий четырежды;
г) ветвь гиперболы 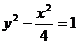 , расположенная в нижней полуплоскости и направленная слева направо. Записать параметрическое уравнение в действительной форме и воспользоваться тождеством
, расположенная в нижней полуплоскости и направленная слева направо. Записать параметрическое уравнение в действительной форме и воспользоваться тождеством  ;
;
д) прямолинейный отрезок, идущий из точки 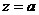 в точку
в точку  ;
;
е) окружность единичного радиуса с центром в точке 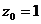 , обходимая один раз по часовой стрелке.
, обходимая один раз по часовой стрелке.
7. а) Внешность круга с центром в точке 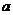 радиуса
радиуса 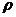 ;
;
б) верхняя полуплоскость.
Занятия 5, 6. Условия Коши – Римана. Геометрический смысл производной
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Если предел
. Если предел

существует и не зависит от способа стремления точки  к точке
к точке  , то функция
, то функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , а значение предела называется производной функции
, а значение предела называется производной функции  в точке
в точке  .
.
Функция, дифференцируемая в некоторой окрестности точки, называется аналитической в этой точке, а функция, аналитическая в каждой точке области, называется аналитической в этой области.
Функция
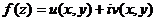
аналитична в области 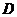 тогда и только тогда, когда функции
тогда и только тогда, когда функции  непрерывны в области
непрерывны в области 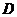 и удовлетворяют там условиям Коши – Римана
и удовлетворяют там условиям Коши – Римана
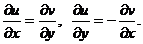
Известно, что аналитическая функция бесконечно дифференцируема.
Производную 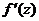 можно вычислить по любой из следующих формул:
можно вычислить по любой из следующих формул:
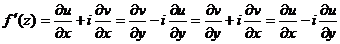 .
.
Формулы вычисления производных основных элементарных функций комплексной переменной аналогичны соответствующим формулам дифференцирования функций действительной переменной:
 ;
; 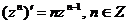 ;
; 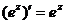 ;
;
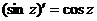 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
Действительная функция  называется гармонической в области, если она имеет в этой области непрерывные частные производные до второго порядка включительно и удовлетворяет уравнению Лапласа:
называется гармонической в области, если она имеет в этой области непрерывные частные производные до второго порядка включительно и удовлетворяет уравнению Лапласа:
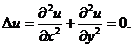
Две гармонические функции  и
и  , удовлетворяющие условиям Коши – Римана, называются сопряженными.
, удовлетворяющие условиям Коши – Римана, называются сопряженными.
Очевидно, если  – сопряженные гармонические функции в области
– сопряженные гармонические функции в области 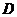 , то функция
, то функция 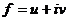 аналитична в области
аналитична в области 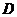 .
.
Действительная функция двух действительных переменных является действительной или мнимой частью аналитической функции тогда и только тогда, когда она является гармонической, для которой сопряженная с ней гармоническая функция находится из условий Коши – Римана.
Если функция  аналитична в точке
аналитична в точке  и
и  , то все гладкие кривые, проходящие через точку
, то все гладкие кривые, проходящие через точку  , поворачиваются при отображении
, поворачиваются при отображении  на один и тот же угол
на один и тот же угол  (угол поворота) и линейное растяжение по всем направлениям, выходящим из точки
(угол поворота) и линейное растяжение по всем направлениям, выходящим из точки  , одинаково и равно
, одинаково и равно  (коэффициент линейного растяжения).
(коэффициент линейного растяжения).