Чайковский филиал
Федерального государственного бюджетного
Образовательного учреждения высшего профессионального образования
"Пермский национальный исследовательский политехнический университет"
(ЧФ ПНИПУ)
Кафедра
Термодинамика
Компьютерная лабораторная работа № 6
“Изучение распределения Максвелла”
Теоретическая часть
1. Опытный факт. Изолированная термодинамическая система с течением времени приходит в равновесное состояние, в котором остается неограниченно долго. Равновесное состояние характеризуется температурой 
.
2. В равновесном состоянии скорости молекул газа распределены по закону, который называется распределением Максвелла. Имеется два варианта этого закона. Распределение Максвелла по абсолютным скоростям и распределение Максвелла по компоненте скорости.
3. Распределения Максвелла по абсолютным скоростям имеет вид
, (1)
где 
– постоянная Больцмана, 
– абсолютная температура газа, 
– масса молекулы.
Для практических вычислений удобно записать распределение (1) в виде
, (2)
где 
- молярная масса газа, а 
- газовая постоянная.
Sic! Значение молярной массы 
берется в килограммах! Поэтому, значение молярной массы, взятое из таблицы Менделеева, умножаем на множитель 
.
4. Распределение Максвелла показывает, какая доля молекул 
от общего числа молекул 
обладает скоростью лежащей в малом интервале скоростей от 
до 
.
5. Если вычислить интеграл от распределения Максвелла (2)
, (3)
то мы узнаем, какая доля молекул 
от их полного числа 
обладает скоростью, лежащей в интервале от 
до 
, т.е. уже не в малом, а в любом фиксированном интервале.
Смысл формулы (3) можно пояснить следующим образом. Если из газа находящегося при температуре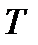 
взять наугад молекулу, то с вероятностью 
, она будет иметь абсолютную скорость, лежащую в интервале от до .
6. Очевидно, что все молекулы имеют абсолютную скорость от 
до 
, поэтому
. (4)
Множитель
называется нормировочным множителем. Он обеспечивает равенство интеграла (4) единице.
7. Функция
, (5)
входящая в выражения (1) – (4) называется плотностью распределения молекул по абсолютным скоростям. График функции (5) представлен на рис.1.
| Рис. 1. |
8. Функция плотности распределения (5) достигает максимума при значении скорости
, (6)которая называется наиболее вероятной скоростью.
Кроме наиболее вероятной скорости, выделяют:
- среднюю арифметическую скорость; (7)
- среднюю квадратичную скорость. (8)
Соотношение между скоростями
.
9. Пусть нас интересует не абсолютное значение скорости, а её составляющая вдоль какого-либо направления, например 
, иными словами мы будем учитывать не только величину, но направление скорости. Тогда, закон распределения молекул газа для компоненты скорости будет иметь вид
. (9)
или в форме, удобной для вычисления
9. Интеграл от закона распределения (9)
(10)
показывает какая доля молекул от их полного числа обладает скоростью, лежащей в интервале от до , с учетом направления движения. Например, какая часть молекул от их общего числа обладает скоростью от 
до 
.
10. Как и в случае абсолютной скорости, вероятность любой составляющей скорости для молекулы газа равна единице, поэтому
, (11)
- нормировочный множитель.
11. Функция плотности распределения молекул по z – компоненте скорости
. (12)
График функции (8) имеет вид Гауссова колокола (рис.2)
| Рис. 2. |
Практическая часть
На основе теоретическую часть, разработать компьютерную модель и проводя численный эксперимент изучить распределение Максвелла в следующей последовательности.
1. Составить программу для построения графиков функций распределения Максвелла. Предусмотреть вычисление машиной наиболее вероятной скорости, средней скорости и средней квадратичной скорости. Газ и его исходную температуру взять согласно варианту.
2. Построить графики функции распределения Максвелла для абсолютных скоростей молекул 
и для составляющей скорости 
. Сравнить оба графика, объяснить их различие и смысл.
3. Построить графики вероятностных функций 
и 
в интервалах скоростей 
и 
, соответственно. Убедится, что вероятность в обоих случаях равна единице.
4. Построить графики функции распределения Максвелла для абсолютных скоростей молекул и для составляющей скорости при различных температурах газа. Проанализировать характер изменения графиков и сделать вывод о характере изменения скоростей молекул газа.
Построить графики функции распределения Максвелла для абсолютных скоростей молекул и для составляющей скорости 
, для газов различной молярной массы 
, при одной и той же температуре. Сделать выводы о характере распределения молекул по скоростям для легких и тяжелых газов.
Сделать общее заключение.
Таблица вариантов
| № варианта | Газ | Исходная температура эксперимента | ||
| гелий | ||||
| неон | ||||
| аргон | ||||
| кислород | ||||
| азот | ||||
| углекислый газ | ||||
| аммиак | ||||
| ацетилен | ||||
| окись азота | ||||
| метан | ||||
| этан | ||||
| этилен | ||||
| криптон | -10 | |||
| хлор | ||||
| фтор | ||||
| ксенон | -20 | |||
| двуокись серы | ||||
| окись углерода | ||||
| воздух | ||||
| двуокись азота | ||||
| водяной пар |
Пояснения для выполнения работы.
Распределение Максвелла
Математическая модель
- плотность распределения Максвелла по абсолютной скорости
, - плотность распределения Максвелла по z-компоненте скорости
, - наиболее вероятная скорость; (3)
- средняя арифметическая скорость; (4)
- средняя квадратичная скорость. (5)
- вероятность попадания в интервал абсолютных
скоростей
- вероятность попадания в интервал z – составляющей скоростей
Пример блока построения графиков компьютерной модели для водорода при температуре 
. Молярная масса водорода 
.
// Распределение Максвелла
tt:=0.01; {шаг счета, равный шагу приращения скорости}
mm:= 2*0.001; {молярная масса в кг (водород)}
Tk:=273.15; {температура газа}
C:=Sqrt(2/Pi)*Power((mm/(R*Tk)),3/2); {нормировочная константа абсолютной
скорости}
Cz:=Sqrt(mm/(2*Pi*R*Tk)); {нормировочная константа z – составляющей
скорости}
VP:=Trunc(Sqrt(2*R*Tk/mm)); {наиболее вероятная скорость молекул}
V0:=Trunc(Sqrt(8*R*Tk/(Pi*mm))); {средняя скорость молекул}
VV:=Trunc(Sqrt(3*R*Tk/mm)); {средняя квадратичная скорость молекул}
WW:=0; {плотность распределения по абсолютной скорости}
W:=0; {плотность распределения по z – компоненте скорости}
v:=0; {скорость молекул}
P:=0; {вероятность попадания в интервал абсолютных скоростей}
PZ:=0; {вероятность попадания в z – интервал скоростей}
// Распределение по абсолютным скоростям
For i:=1 to 600000 do
begin
v:=v+tt;
ww:=C*Exp(-mm/(2*R*Tk)*Sqr(v))*Sqr(v);
P:=p+ww*tt;
SetPixel(X0+round(v*40*MasX),Y0-round(ww*40*MasY), clBlack);
SetPixel(X0+round(v*40*MasX),Y0-round(P*40*MasY1), clBlack);
end;
// Распределение по Z- компоненте
v:=-9000;
w:=0;
For i:=1 to 2000000 do
begin
v:=v+tt;
w:=Cz*Exp(-mm/(2*R*Tk)*Sqr(v));
PZ:=PZ+w*tt;
SetPixel(X0+round(v*40*MasX1),Y0-round(w*40*MasY), clBlack);
SetPixel(X0+round(v*40*MasX1),Y0-round(PZ*40*MasY1), clBlack);
end;
На рисунке 3 приведены графики распределений по скоростям и вероятности попадания в интервалы. На рисунке 4, 5 приведены графики зависимостей распределений от температуры газа (водорода), а на рисунках 6, 7, – зависимости распределений от молярной массы газа.
| Рис. 3. |
| Рис. 4. |
| Рис. 5. |
| Рис. 6. |
| Рис. 7. |