Вычислить
,
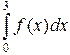где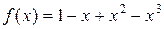 
.
Здесь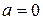 
и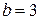 
.
Пусть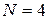 
, тогда 
.
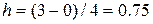Метод прямоугольников.
Имеем: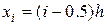 
, 
, 
.
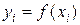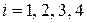Расчет сведен в табличную форму.
| 
| 
|
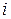
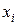
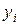
| 0.375 | 0.713 | |
| 1.125 | –0.283 | |
| 1.875 | –3.951 | |
| 2.625 | –12.822 |
На основании данных, приведенных в таблице, вычисляем приближенное значение интеграла по формуле средних прямоугольников (2.5.6):
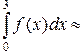0.75·[0.713+(–0.283)+(–3.951)+(–12.822)]=-12.258
Метод трапеций.
Имеем: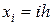 
, , 
.
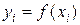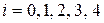Расчет сведен в табличную форму
|
|
|
|
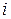
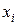
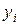
| 0.0 | 1.0 | |
| 0.75 | 0.391 | |
| 1.5 | –1.625 | |
| 2.25 | –7.578 | |
| 3.0 | –20.0 |
На основании данных, приведенных в таблице, вычисляем приближенное значение интеграла по формуле трапеций (2.5.12):
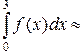0.75·{[1.0+(–20.0)]/2+0.391+(–1.625)+(–7.578)}=–13.734
Метод Симпсона.
Аналогично методу трапеций:
, , .
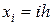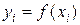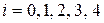Расчет сведен в табличную форму (таблицы метода трапеций и метода Симпсона совпадают).
|
|
|
|
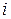
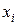
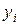
| 0.0 | 1.0 | |
| 0.75 | 0.391 | |
| 1.5 | –1.625 | |
| 2.25 | –7.578 | |
| 3.0 | –20.0 |
На основании данных, приведенных в таблице, вычисляем приближенное значение интеграла по формуле Симпсона (3.5.18):
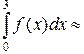0.75/3·[1.0+4·0.391+2 (–1.625)+4 (–7.578)+(–20.0)]=-12.749
Пример программы (лабораторная работа 5).
Вычисление интеграла методами прямоугольников (средних), трапеций и Симпсона с заданной точностью.
Варианты задания.
,
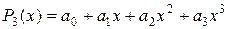где
, 
, 
, 
, 
,
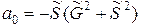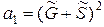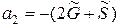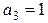
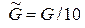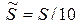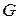– номер группы; 
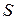– номер студента по журналу.
Текст программы на F90
| function f(x) common a0,a1,a2 f=((x+a2)*x+a1)*x+a0 end ! метод прямоугольников function pr(a,b,n) h=(b-a)/n; s=0; x=a+h/2 do i=1,n s=s+f(x); x=x+h enddo; pr=h*s end ! метод трапеций function tr(a,b,n) h=(b-a)/n; s=(f(a)+f(b))/2; x=a+h do i=1,n-1 s=s+f(x); x=x+h enddo; tr=h*s end ! метод Симпсона function simps(a,b,n) h=(b-a)/n; s=f(a)+f(b); x=a+h; z=1 do i=1,n-1 s=s+(3+z)*f(x); x=x+h; z=-z enddo; simps=h*s/3 end function aintegral(a,b,eps,kmax,n,sint) n=2; s=sint(a,b,n) do k=0,kmax n=n*2; s1=sint(a,b,n); if(abs(s1-s)<eps) goto 1; s=s1 enddo 1 aintegral=s1 end external f,pr,tr,simps parameter(s=17,g=3,eps=0.0001,kmax=20,a=0,b=3) common a0,a1,a2 real r(20) a0=-s*(g*g+s*s)/1000; a1=(s+g)**2/100; a2=-(2*g+s)/10; print '(4(2x,a,f10.4))','a0=',a0,'a1=',a1,'a2=',a2 print 100,'PR:',aintegral(a,b,eps,kmax,n,pr),'n=',n print 100,'TR:',aintegral(a,b,eps,kmax,n,tr),'n=',n print 100,'SIMPS:',aintegral(a,b,eps,kmax,n,simps),'n=',n call qatr(a,b,eps,20,f,sq,ier,r); print 100,'QATR:',sq 100 format(2x,a,f10.4,4x,a,i10) end |
Результаты счета
a0= -5.0660 a1= 4.0000 a2= -2.3000
PR: 2.3520 n= 512
TR: 2.3520 n= 1024
SIMPS: 2.3520 n= 4
QATR: 2.3520
Press any key to continue
Замечание.
1. В приведенной программе реализованы все три рассматриваемые в настоящем курсе формулы численного интегрирования:
- п/п PR – вычисление интеграла по формуле прямоугольников;
- п/п TR – вычисление интеграла по формуле трапеций;
- п/п SIMPS – вычисление интеграла по формуле Симпсона.
2. Переменная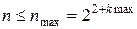 
(в программе – kmax) определяет количество отрезков, на которые делится интервал интегрирования для вычисления интеграла с заданной точностью. При этом значение n последовательно удваивается до тех пор, пока изменение приближенного значения интеграла не станет меньше заданного малого числа 
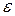(в программе – eps), значение которого вводится. При расчете было принято:
kmax =20, eps =0.0001.
3. К данной программе (проекту) необходимо подключить стандартную подпрограмму QATR.FOR.
4. Формальному параметру sint (имени подпрограммы) в подпрограмме-функции aintegral соответствуют фактические параметры pr,tr и simps (имена подпрограмм-функций). Эти параметры, а также фактический параметр f в обращении к стандартной подпрограмме qatr, должны быть перечислены в списке оператора external:
external f,pr,tr,simps.
5. Параметры a0,a1,a2 вычисляются в основной программе и передаются в подпрограмму-функцию f оператором общих областей common:
common a0,a1,a2.