Вопросы к зачёту (1 курс 1 семестр)
1. Предмет линейной алгебры. Определитель второго и третьего порядка. Способы вычисления.
2. Минор и алгебраическое дополнение элемента определителя. Свойства определителей.
3. Определитель n-го порядка. Вычисление определителя n-го порядка способом разложения по строке или столбцу
4. Матрицы: определение, виды матриц, элементарные преобразования матриц.
5. Действия над матрицами.
6. Ранг матрицы. Способы нахождения ранга.
7. Обратная матрица. Алгоритм нахождения обратной матрицы.
8. Системы линейных уравнений: определение, общий вид, решение. Совместная и несовместная, определённая и неопределённая системы линейных уравнений.
9. Элементарные преобразования систем линейных уравнений. Эквивалентные системы.
10. Матрица системы. Расширенная матрица системы. Теорема Кронекера-Капелли.
11. Матричный способ решения системы линейных уравнений.
12. Метод Крамера.
13. Метод Гаусса.
14. Системы однородных линейных уравнений.
15. Математическая модель межотраслевого баланса Леонтьева.
16. Основные понятия векторной алгебры: определение вектора (геометрическое и арифметическое), координаты вектора, модуль вектора, нуль-вектор, равенство векторов, орт вектора. Коллинеарные и компланарные вектора.
17. Линейные операции над векторами: сложение, умножение вектора на число, и их свойства.
18. Арифметическое n-мерное векторное пространство 
. Линейное пространство общего вида.
19. Скалярное произведение векторов и его свойства. Косинус угла между векторами. Экономическая и физическая интерпретация скалярного произведения векторов. Эвклидово пространство.
20. Векторное произведение векторов, его свойства и геометрический смысл. Выражение векторного произведения через координаты векторов.
|
|
21. Смешанное произведение векторов, его свойства и геометрический смысл. Выражение смешанного произведения через координаты.
22. Собственные векторы, собственные значения матриц. Линейная модель обмена.
23. Система координат на плоскости. Прямоугольная декартовая система координат. Полярная система координат.
24. Уравнения прямых на плоскости. Уравнение прямой с заданным угловым коэффициентом. Общее уравнение прямой. Каноническое уравнение прямой. Уравнение прямой, перпендикулярной данному вектору. Уравнение прямой, проходящей через две данные точки.
25. Расстояние и угол между двумя прямыми.
26. Общее уравнение кривых 2-го порядка. Уравнение окружности, эллипса, гиперболы и их свойства.
27. Уравнение параболы и её свойства. Общее уравнение плоскости в пространстве. Расстояние от точки до плоскости.
28. Функция: определение, область определения и область значения, график функции. Свойства функций. Виды элементарных функций. Преобразование графиков функций. Функции в экономике
29. Последовательность. Предел последовательности.
30. Определение предела функций в точке на языке 
(определение Коши)
31. Бесконечно малая функция (величина). Свойства бесконечно малых величин. Бесконечно большая функция.
32. Первый и второй замечательные пределы (доказательство 1го).
33. Основные теоремы о пределах функции в точке (доказательство одной из них).
34. Способы раскрытия неопределенности вида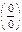 
при вычислении пределов функции в точке.
|
|
35. Определение предела функции в бесконечности. Раскрытие неопределенности вида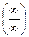 
36. Применение теории пределов в теории управления.
Вопросы к зачёту (1 курс 2 семестр)
1. Непрерывность функции в точке и на промежутке.
2. Теоремы о непрерывных функциях.
3. Односторонние пределы функции. Точки разрыва функции I и II рода.
4. Свойства функций непрерывных на отрезке (теоремы Вейерштрасса и Больцано-Коши).
5. Производная функции одной переменной, ее механический, геометрический и экономический смысл.
6. Производная суммы, частного, произведения (доказательств одной из формул).
7. Производная сложной функции. Дифференцирование неявно заданной функции.
8. Дифференциал функции одной переменной и его геометрический смысл.
9. Применение дифференциала для приближенных вычислений.
10. Применение первой и второй производной к исследованию функций.
11. Асимптоты графика функции.
12. Исследование функции по полному плану.
13. Применение дифференциального исчисления для решения экономических и управленческих задач.
14. Первообразная, неопределенный интеграл и его свойства.
15. Формулы интегрирования. Непосредственное интегрирование.
16. Интегрирование способом замены переменной.
17. Интегрирование по частям (вывод формулы).
18. Определение определенного интеграла и его геометрический смысл.
19. Основные свойства определенного интеграла. Формула Ньютона-Лейбница.
20. Применение определенного интеграла для вычисления площадей плоских фигур.
21. Вычисление объемов тел вращения с помощью определенного интеграла.
|
|
22. Экономические приложения определённого интеграла.
23. Определение интегралов с бесконечными пределами. Применение основной формулы интегрального исчисления к несобственным интегралам.
24. Определение функции двух переменных. Область определения. График. Линии уровня.
25. Предел функции двух переменных в точке.
26. Непрерывность функции двух переменных.
27. Свойства функций, непрерывных в ограниченной замкнутой области.
28. Частные производные первого порядка и их геометрическое истолкование.
29. Полный дифференциал функции двух переменных и его применение к приближённым вычислениям.
30. Частные производные высших порядков. Дифференциалы высших порядков.
31. Экстремум функции двух переменных. Необходимое и достаточные условия экстремума.
32. Применение полного дифференциала к приближенным вычислениям.
33. Наибольшее и наименьшее значения функции двух переменных в замкнутой области.
Вопросы к экзамену (2 курс 1 семестр)
1. Определитель n-го порядка. Вычисление определителя n-го порядка способом разложения по строке или столбцу. Минор и алгебраическое дополнение элемента определителя.
2. Матрицы, виды матриц, элементарные преобразования матриц. Действия над матрицами. Ранг матрицы.
3. Обратная матрица. Алгоритм нахождения обратной матрицы.
4. Системы линейных уравнений. Методы решения: матричный, Крамера, Гаусса.
5. Предел функции в точке. Способы вычисления предела функции в точке и на бесконечности. Замечательные пределы.
6. Непрерывность функции в точке и на промежутке. Точки разрыва функции.
7. Дифференцирование функции одной переменной. Правила и формулы вычисления производной. Вычисление производной неявно заданной функции. Дифференциал функции одной переменной.
8. Неопределенный интеграл. Формулы и методы интегрирования.
9. Определенный интеграл. Формула Ньютона-Лейбница. Применение определенного интеграла. Несобственные интегралы.
10. Дифференциальные уравнения: порядок, решение ДУ, общее и частное решение, задача Коши, интегральная кривая. ДУ первого порядка.
11. Дифференциальные уравнения второго порядка: допускающие понижение порядка и линейные однородные с постоянными коэффициентами.
12. Функция двух переменных. Область определения. График. Линии уровня. Частные производные первого и второго порядка. Полный дифференциал.
13. Экстремум функции двух переменных. Необходимое и достаточные условия экстремума.
14. Числовые ряды: общий член, частичная сумма, сходимость и расходимость рада. Примеры рядов. Необходимое и достаточные условия сходимости знакопостоянных числовых рядов.
15. Знакопеременные ряды. Условная и абсолютная сходимость знакопеременных рядов. Признак Лейбница.
16. Функциональные ряды. Степенной ряд. Радиус сходимости степенного ряда. Ряд Тейлора, ряд Маклорена. Разложение функций в ряд Маклорена..
17. Предмет теории вероятностей. Начальные понятия: испытание, событие, виды событий, несовместные и совместные, противоположные события, элементарные события, полная группа событий, равновозможные и благоприятные события.
18. Определение вероятности события (статическое, классическое, геометрическое).
19. Сумма событий. Теорема сложения вероятностей и следствия из неё.
20. Произведение событий. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей.
21. Формула полной вероятности. Формула Байеса.
22. Независимые испытания. Повторение испытаний. Формула Бернулли. Предельные теоремы в схеме Бернулли.
23. Случайная величина. Дискретная случайная величина и ее закон распределения. Многоугольник распределения DCB. Числовые характеристики DCB случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение.
24. Функция распределения случайной величины и её свойства.
25. Виды распределения дискретной случайной величины: биномиальное, распределение Пуассона.
26. Непрерывная случайная величина (НСВ). Функция плотности вероятности непрерывной случайной величины и её свойства. Числовые характеристики НCB случайной величины.
27. Виды распределения непрерывной случайной величины: равномерное, показательное, нормальное.
28. Вероятность попадания непрерывной случайной величины в заданный интервал. Вероятность попадания нормально распределенной НСВ в заданный интервал.
29. Предельные теоремы теории вероятностей. Закон больших чисел. Центральная предельная теорема.
30. Двумерная случайная величина. Закон распределения двумерной случайной величины.
31. Независимые случайные величины. Операции над независимыми случайными величинами.
32. Зависимые случайные величины Условные законы распределения двумерной случайной величины.
33. Числовые характеристики двумерной случайной величины: математическое ожидание М(X;Y), ковариация cov(X,Y).
34. Коэффициент корреляции двух случайных величин и его свойства.
35. Регрессия. Линия регрессии. Линейная регрессия.
36. Предмет математической статистики. Основные задачи математической статистики. Генеральная и выборочная совокупность. Виды выборок. Способы отбора. Репрезентативность выборки.
37. Вариационный ряд. Частота и относительная частота (частость) варианты выборки. Статистическое распределение выборки: статистический ряд частот и относительных частот. Полигон частот.
38. Интервальный статистический ряд. Гистограмма.
39. Эмпирическая функция распределения.
40. Числовые характеристики статистического распределения и вариационного ряда.
41. Оценка неизвестных параметров. Свойства статистических оценок. Точечные оценки параметров генеральной совокупности.
42. Интервальное оценивание параметров. Доверительные интервалы. Доверительные интервалы для параметров нормально распределённой случайной величины.
43. Статистическая гипотеза. Виды гипотез. Статистический критерий. Ошибки при проверке гипотез.
44. Методика проверки гипотез. Проверка гипотезы о нормальности распределения генеральной совокупности. Критерий Пирсона.
Пример практических заданий к экзамену:
| xi | ||||
| ni |
1.Статистическое распределение частот выборки задано таблицей.
Найдите объём выборки. Задайте таблицей статистическое
распределение относительных частот. Найдите среднее выборочное и выборочную дисперсию.
2.. Для данной реализации выборки 50122310045551442143 построить вариационный ряд. Найти размах вариаций, моду и медиану вариационного ряда.
3. Случайная величина X задана функцией распределения 
Вычислить: а) вероятность попадания случайной величины X в интервалы (1; 2,5) и (2,5; 3,5);
б) числовые характеристики данной случайной величины.
4.Случайная величина Х задана дифференциальной функцией распределения 
По какому закону распределена случайная величина? Найти М(х), D(х), (х), F(х), Р(0<Х<2).
5. Пусть средний рост человека равен 170 см, а среднее квадратическое отклонение равно 9 см.
а) Полагая, что рост человека имеет нормальное распределение, найти количество людей, имеющих рост от 150 до 195 см. б) найти количество человек с ростом меньшим 165см.
6. Найдите асимптоты графика функции 
7. Вычислите: 
8.Найдите полный дифференциал функции двух переменных Z= f(x;y), если Z= 
9. Решите дифференциальное уравнение с разделяющимися переменными 
, если 
.
10. Найдите произведение матриц А и В, если 