Контрольная работа №1.
Тема 1. Множества. Действительные числа.
1. Основные понятия. Литература: [3], §13, п. 13.1.
2. Числовые множества. Множество действительных чисел. Литература: [3], §13, п. 13.2.
3. Числовые промежутки. Окрестность точки. Литература: [3], §13, п. 13.3.
Тема 2. Функции
1. Понятие функции. Литература: [3], §14, п. 14.1.
2. Числовые функции. График функции. Способы задания функций. Литература: [3], §14, п. 14.2.
3. Основные характеристики функции. Литература: [3], §14, п. 14.3.
4. Обратная функция. Литература: [3], §14, п. 14.4.
5. Сложная функция. Литература: [3], §14, п. 14.5.
6. Основные элементарные функции и их графики. Литература: [3], §14, п. 14.6.
Тема 3. Последовательности
1. Числовая последовательность. Литература: [3], §15, п. 15.1.
2. Предел числовой последовательности. Литература: [3], §15, п. 15.2.
3. Предел монотонной ограниченной последовательности.
Число е. Натуральные логарифмы. Литература: [3], §15, п. 15.4.
Тема 4. Предел функции
1. Предел функции в точке. Литература: [3], §16, п. 16.1.
2. Односторонние пределы. Литература: [3], §16, п. 16.2.
3. Предел функции при  Литература: [3], §16, п. 16.3.
Литература: [3], §16, п. 16.3.
4. Основные теоремы о пределах. Литература: [3], §17, п. 17.3.
5. Замечательные пределы. Литература: [3], §17, п. 17.5, 17.6.
Тема 5. Непрерывность функций
1. Непрерывность функции в точке. Литература: [3], §19, п. 19.1.
2. Непрерывность функции в интервале и на отрезке. Литература: [3], §19, п. 19.2.
3. Точки разрыва функции и их классификация. Литература: [3], §19, п. 19.3.
4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций. Литература: [3], §19, п. 19.4.
Тема 6. Производная функции
1. Определение производной, ее механический и геометрический смысл. Уравнение касательной и нормали к кривой. Литература: [3], §20, п. 20.2.
2. Производная суммы, разности, произведения и частного функций. Литература: [3], §20, п. 20.4.
3. Производная сложной и обратной функций. Литература: [3], §20, п. 20.5
4. Таблица производных. Литература: [3], §20, п. 20.8.
5. Дифференцирование неявных и параметрически заданных функций. Литература: [3], §21.
6. Производные высших порядков явно заданной функции. Литература: [3], §23, п. 23.1.
Тема 7. Дифференциал функции
1. Понятие дифференциала функции. Литература: [3], §24, п. 24.1.
2. Геометрический смысл дифференциала функции. Литература: [3], §24, п. 24.2.
3. Основные теоремы о дифференциалах. Литература: [3], §24, п. 24.3.
Тема 8. Исследование функций
1. Основные теоремы дифференциального исчисления. Литература: [3], §25, п. 25.1.
2. Правило Лопиталя. Литература: [3], §25, п. 25.2.
3. Возрастание и убывание функций. Максимум и минимум функций. Литература: [3], §25, п. 25.3, 25.4.
4. Наибольшее и наименьшее значения функции на отрезке. Литература: [3], §25, п. 25.5.
5. Выпуклость графика функции. Точки перегиба. Литература: [3], §25, п. 25.6.
6. Общая схема исследования функции и построения графика. Литература: [3], §25, п. 25.7.
Тема 9. Формула Тейлора
Литература: [3], §26. При решении задач 91-100 полезно использовать формулу Лейбница, которая позволяет вычислить производную n-го порядка от произведения двух функций ([1], гл. III, §22). 
Контрольная работа №2.
Тема 1. Неопределенный интеграл
1. Понятие неопределенного интеграла. Свойства неопределенного интеграла. Таблица основных неопределенных интегралов. Литература: [3], §29, п. 29.1–29.3.
2. Основные методы интегрирования. Литература: [3], §30, п. 30.1–30.3.
3. Интегрирование рациональных функций. Литература: [3], §31, п. 31.1–31.3.
4. Интегрирование тригонометрических функций. Литература: [3], §32, п. 32.1–32.3. При решении задач 31-40 можно использовать подстановку 
Тема 2. Определенный интеграл
1. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. Свойства определенного интеграла. Литература: [3], §36-38.
2. Вычисление определенного интеграла. Литература: [3], §39, п. 39.1-39.3.
3. Геометрические и физические приложения определенного интеграла. Литература: [3], §41, п. 41.2-41.5.
Тема 3. Несобственные интегралы
Литература: [3], §40, п. 40.1, 40.2.
Ниже приведена таблица номеров заданий, входящих в каждую контрольную работу. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки.
| Вариант | Номера задач контрольных заданий | |||||||||
Задания контрольной работы №1
В задачах 1-10 найти предел последовательности.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
В задачах 11-20 вычислить предел.
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
В задачах 21-25 определить, при каких значениях а функция f(x) непрерывна на всей числовой оси.
21. 
22. 
23. 
24. 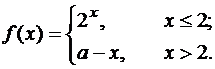
25. 
В задачах 26-30 определить точки и характер разрыва функции.
26.  ; 27.
; 27. 
28.  ; 29.
; 29. 
30.  .
.
В задачах 31-40 найти значение производной функции y=f(x) в точке х0.
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
37.  38.
38. 
39.  40.
40. 
41. Составить уравнения касательных к гиперболе  в точках, в которых эти касательные перпендикулярны прямой у=1-2х. Сделать чертеж.
в точках, в которых эти касательные перпендикулярны прямой у=1-2х. Сделать чертеж.
42. Написать уравнение прямой, проходящей через точку (1;2) параллельно касательной к графику функции  , проведенной в точке с абсциссой х=1. Сделать чертеж.
, проведенной в точке с абсциссой х=1. Сделать чертеж.
43. На кривой  найти точки, в которых касательные к кривой параллельны прямой у=6х-5. Составить уравнения этих касательных. Сделать чертеж.
найти точки, в которых касательные к кривой параллельны прямой у=6х-5. Составить уравнения этих касательных. Сделать чертеж.
44. Показать, что касательные, проведенные к гиперболе  в точках пересечения с осями координат, параллельны между собой. Найти уравнения касательных. Сделать чертеж.
в точках пересечения с осями координат, параллельны между собой. Найти уравнения касательных. Сделать чертеж.
45. Составить уравнение прямой, перпендикулярной касательной, проведенной к гиперболе  в точке с абсциссой х=-1, и проходящей через эту точку. Сделать чертеж.
в точке с абсциссой х=-1, и проходящей через эту точку. Сделать чертеж.
46. К гиперболе  проведены две параллельные касательные, одна из которых проходит через точку (6;-1), принадлежащую гиперболе. Составить уравнение второй касательной. Сделать чертеж.
проведены две параллельные касательные, одна из которых проходит через точку (6;-1), принадлежащую гиперболе. Составить уравнение второй касательной. Сделать чертеж.
47. Составить уравнение касательной к параболе у=х2-4х+5, если известно, что эта касательная проходит через точку (0;4) и абсцисса точки касания положительна. Сделать чертеж.
48. Написать уравнение прямой, проходящей через начало координат и точку пересечения касательных к параболе у=х2-х в точках с ординатой у=2. Сделать чертеж.
49. Составить уравнения касательных к гиперболе  , параллельных прямой 3х-у+2=0. Сделать чертеж.
, параллельных прямой 3х-у+2=0. Сделать чертеж.
50. Выяснить, в каких точках касательные к гиперболе  образуют с осью Ох угол 1350. Составить уравнения этих касательных. Сделать чертеж.
образуют с осью Ох угол 1350. Составить уравнения этих касательных. Сделать чертеж.
В задачах 51-60 найти производную функции, заданной параметрически.
51.  52.
52. 
53.  54.
54. 
55.  56.
56. 
57.  58.
58. 
59.  60.
60. 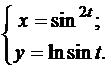
В задачах 61-65 определить интервал, в котором возрастает функция.
61.  62.
62.  63.
63.  64.
64.  65.
65. 
В задачах 66-70 определить интервал, в котором убывает функция.
66.  67.
67. 
68.  69.
69. 
70. 
В задачах 71-80 определить сумму наименьшего и наибольшего значений функции f(x) на отрезке [a;b].
71. 
72. 
73. 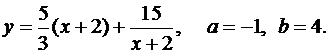
74. 
75. 
76. 
77. 
78. 
79. 
80. 
В задачах 81-90 исследовать функцию и построить схематично ее график.
81.  82.
82. 
83.  84.
84. 
85.  86.
86. 
87.  88.
88. 
89.  90.
90. 
В задачах 91-100 найти коэффициент при хn в разложении функции y=f(x) по формуле Маклорена.
91.  92.
92. 
93.  94.
94. 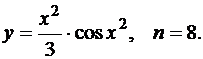
95.  96.
96. 
97. 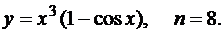 98.
98. 
99.  100.
100. 