Полученная система уравнений представляет собой систему обыкновенных дифференциальных уравнений, общий вид которой может быть представлен следующим образом:
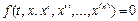, где x=x(t) – неизвестная функция.
Решением дифференциального уравнения является поиск такой функции x=x(t), при подстановке которой в это уравнение получается тождество.
При решении подобного рода уравнений в первую очередь необходимо уравнения высших порядков привести к системе уравнений первого порядка. Например, уравнение второго порядка
можно переписать в следующем виде
,
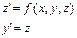где z – новая зависимая переменная, определяемая вторым уравнением. Теперь мы имеем систему уравнений относительно y и z. Решение этой системы дает функцию и ее производную.
В данном случае, переходя от системы уравнений (3) к системе уравнений (9) мы использовали зависимости (7) и (8), поэтому итоговая система уравнений (9) является системой уравнений первого порядка.
В качестве примера рассмотрим приближенное решение дифференциального уравнения первого порядка методом Эйлера:
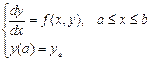. (10)
Заменяя производную в окрестности каждого i -го узла сетки разностным отношением, приходим к следующему виду уравнения:
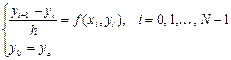. (11)
Последовательные значения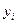 
определяются по формуле
.
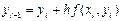Метод Эйлера имеет очень простую геометрическую интерпретацию. Искомая интегральная кривая у(х) на отрезке [а; b] приближается к ломаной (рисунок 2), наклон которой на каждом элементарном участке [хi, хi+1] определяется наклоном интегральной кривой уравнения в точке (хi, уi).
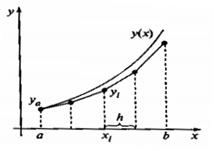
Рисунок 2 – Графическая интерпретация метода Эйлера
В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, т.е. построения таблицы приближенных значений функции у=у(х), удовлетворяющей заданным начальным условиям, где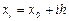 
, 
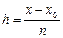- шаг таблицы.
|
|
| x | x1 | x2 | x3 | … | xn |
| y | y1 | y2 | y3 | … | yn |
Приближенно можно считать, что правая часть в 
остается постоянной на каждом из отрезков между точками деления. Метод Эйлера состоит в непосредственной замене производной разностными отношениями по приближенной формуле
;
.
Таким образом, если x=x1, то
;
если x=x2, то
;
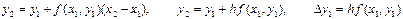если x=xi+1, то
;
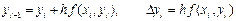Таким образом, получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом применении пары формул
, (12)
где i=0, 1, 2,…n.
Геометрически эти формулы означают, что на отрезке [хi; хi+1] интегральная кривая заменяется отрезком касательной к кривой (рисунок 3).
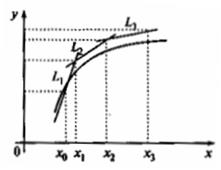
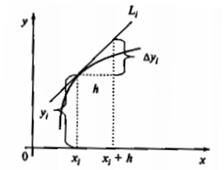
а – интегральная кривая б – касательная к кривой
Рисунок 3 – Графическая интерпретация метода Эйлера
Применяя метод Эйлера к системе уравнений (9), получим
.
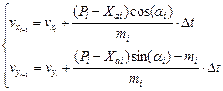Далее, используя зависимость (7) можем найти значения координат ЛА в каждый момент времени и построить график траектории движения ЛА при заданных начальных условиях
.
Метод Эйлера при достаточно малых величинах шага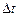 
дает решение с большой точностью, так как погрешность 
на каждом шаге расчета.
ОСНОВНЫЕ ТРЕБОВАНИЯ К КУРСОВОЙ РАБОТЕ