Оценки сложности алгоритма применительно к машинам Тьюринга
Теория сложности зависит от положенных в ее основу уточнений алгоритма и от выбранной меры сложности. Рассмотрим оценки сложности алгоритма применительно к машине Тьюринга.
С каждой конфигурацией k, к которой применима машина Тьюринга М, можно связать число М(k), характеризующее сложность процесса в том или ином смысле. Варьируя k, получим функцию от нее, определенную на множестве всех конфигураций, к которым данная машина применима. Функции такого рода назовем сигнализирующими функциями.
Работу машины Тьюринга М характеризуют следующие сигнализирующие функции:
1. Сигнализирующая времени tM(k) равна числу конфигураций М(k), если М применима к k (длительность процесса) и tM(k) неопределена, если М не применима к k.
2. Сигнализирующая емкости SM(k) равна длине активной зоны процесса М(k), если М применима к k инеопределена, если М не применима к k.
Активной зоной данной конфигурации называется минимальная связная часть ленты, содержащая обозреваемую ячейку и все ячейки, в которых записаны значащие буквы. Активной зоной процесса называется минимальная связная часть ленты, содержащая активные зоны всех его конфигураций.
3. Сигнализирующая колебаний wM(k) равна числу колебаний (изменения направлений) головки за время tM(k), если М применима к k инеопределена в противном случае.
4. Сигнализирующая режима rM(k) равна максимальному числу всех прохождений головки через край ячейки за время tM(k), если М применима к k инеопределена в противном случае.
В частности, если в качестве конфигурации k взяты начальные конфигурации для слова a, то процесс будет характеризоваться сигнализирующими функциями tM(a), SM(a), wM(a), rM(a).
Следующая теорема показывает, что при наличии верхней оценки для какой-нибудь из сигнализирующих и заданных параметрах m – число символов внешнего алфавита и n – число символов внутреннего алфавита, можно получить верхние оценки для остальных сигнализирующих функций.
Теорема. Для любой машины Тьюринга М и любого слова a, к которому она применима, справедливы следующие неравенства:

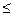
 ;
;

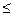
 +1;
+1;
S(a)£ |a| +2nr(a)+1, где |a| — длина слова a;
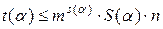 .
.
Нахождение нижних оценок сигнализирующих функций требует специальной теории.
Введенные функции сложности tM(a), SM(a) являются словарными. Удобно ввести для рассмотрения функции натурального аргумента, определив
tM(n)= 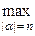 tM(a), SM(n)=
tM(a), SM(n)= 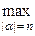 SM(a).
SM(a).
Эти функции также называются функциями временной и ёмкостной сложности (по худшему случаю). Поведение этих функций в пределе при увеличении размера задачи n называется асимптотической временной (соответственно емкостной) сложностью. Для конкретных задач находятся, как правило, асимптотические функции сложности.
Определение класса задач, разрешимых за полиномиальное время (класс сложности P) в терминологии машины Тьюринга. Класс задач NP.
Установление прямых нижних оценок сложности вычислений удаётся лишь в очень редких случаях. В связи с этим вычисления оценивают косвенным путём.
Косвенные нижние оценки – это такие утверждения, в которых существование эффективного разрешающего алгоритма для конкретной задачи влечёт за собой существование эффективного алгоритма для многих общепризнанно трудных задач. Формализуем данный подход.
Пусть П — некоторая массовая задача, I – индивидуальная задача из П (IÎП) и пусть задача I в алфавите А имеет код a(I)ÎА*.
При этом под размером задачи будем понимать длину слова a(I): ça(I)ç. Обозначим через Т машину Тьюринга, решающую задачу П. Тогда tT(n)= 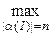 tT(I) — соответствующая функция временной сложности по худшему случаю.
tT(I) — соответствующая функция временной сложности по худшему случаю.
Напомним определение из курса математического анализа.
Определение 1. Говорят, что функция f(n) есть О(g(n)) (читается «О большое от g(n)»), если существует константа с>0 такая, что 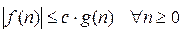 .
.
Определение 2. Говорят, что машина Т решает задачу П за полиномиальное время, если tT(n)=О(p(n)), где p(n) – некоторый полином от n. В противном случае говорят, что задача решается за экспоненциальное время.
Пусть для некоторого класса задач П относительно любой задачи I из П (I  П) ставится вопрос, ответ на который имеет вид “Да ” или “Нет”, т.е. П — класс задач распознавания.
П) ставится вопрос, ответ на который имеет вид “Да ” или “Нет”, т.е. П — класс задач распознавания.
Примеры задач распознавания: 1) Верно ли, что а>b?
2) Верно ли, что х=2∙k? (х – чётное число?)
Определение 3. Говорят, что массовая задача П принадлежит классу NP, если в случае ответа “Да ” для задачи I из П существует слово c(I), длины O(p(ça(I)ç) [|c(I)|=O(p(ça(I)ç))] такое, что задача (I, c(I)) принадлежит классу P. При этом с(I) называют удостоверением или догадкой задачи I.
Наличие догадки позволяет проверить принадлежность задачи I к классу NP.
Пример. Выполнимость формулы алгебры высказываний a(х1, х2, …, хn) проверяется, если кроме самой формулы дан конкретный набор значений переменных х10, х20,…, хn0 – догадка, способствующая установлению выполнимости формулы a.