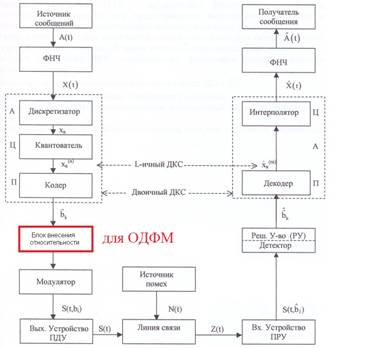
Источник сообщения – это некоторый объект или система, информацию о состояние которой необходимо передать
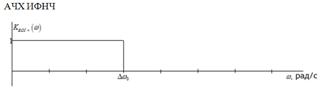
ФНЧ – ограничивает спектр сигнала на верхней частоте FB
Дискретизатор – представляет отклик ФНЧ в виде последовательности отсчетов хk
Квантователь – преобразует отсчеты в квантовые уровни xk(n); k = 0, 1, 2…;
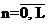 , где L- число уровней квантования.
, где L- число уровней квантования.
Кодер – кодирует квантованные уровни двоичным безызбыточным кодом, т.е. формирует последовательность комбинаций ИКМ bk(n).
Модулятор – формирует сигнал, амплитуда, частота или фаза которого изменяются в соответствии с сигналом bk(n).
Выходное устройство ПДУ – осуществляет фильтрацию и усиление модулированного сигнала для предотвращения внеполосных излучений и обеспечения требуемого соотношения сигнал/шум на входе приемника. Линия связи – среда или технические сооружения по которым сигнал поступает от передатчика к приемнику. В линии связи на сигнал накладывается помеха.
Входное устройство ПРУ – осуществляет фильтрацию принятой смеси – сигнала и помехи.
Детектор – преобразует принятый сигнал в сигнал ИКМ 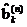 .
.
Декодер – преобразует кодовые комбинации в импульсы
Интерполятор и ФНЧ восстанавливают непрерывный сигнал из импульсов – отсчетов.
Получатель – некоторый объект или система, которому передается информация.
5. АЦП(вариант \4\):
Аналого-цифровое преобразование(АЦП) осуществляется в три этапа. Вначале сообщение дискретизируется по времени, далее квантуется по уровню и затем квантованные уровни кодируются. В результате чего формируется сигнал импульсно-кодовой модуляции(ИКМ).
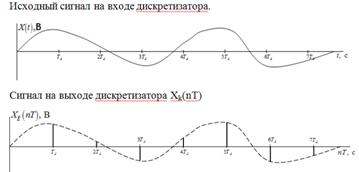
Теоретической основой дискретизации служит теорема Котельникова. Суть её в следующем: любая непрерывная функция x(t), ограниченная по спектру верхней частотой Fв, может быть точно представлена последовательностью своих отсчётов 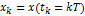 , взятых в моменты времени
, взятых в моменты времени 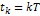 , кратные интервалу дискретизации
, кратные интервалу дискретизации 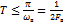 . Отклик x(t) идеального ФНЧ удовлетворяет этой теореме. Поэтому его можно продискретизировать, т.е. преобразовать из аналоговой формы x(t) в дискретно-аналоговую {
. Отклик x(t) идеального ФНЧ удовлетворяет этой теореме. Поэтому его можно продискретизировать, т.е. преобразовать из аналоговой формы x(t) в дискретно-аналоговую { 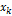 }, с частотой дискретизации
}, с частотой дискретизации 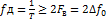 .
.
Дискретизатор можно реализовать в виде перемножителя двух функций: непрерывного сообщения x(t) и периодической последовательности дискретизирующих импульсов 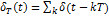 .
.
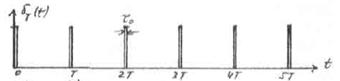 Рис 2а
Рис 2а
Отклик дискретизатора 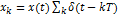 (заштрихованная последовательность импульсов)
(заштрихованная последовательность импульсов)
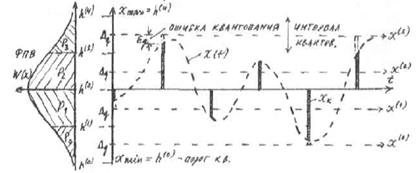
Рис 2б
В момент 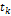 импульсы на выходе дискретизатора могут принимать бесчисленное множество значений из ограниченного или неограниченного диапазона
импульсы на выходе дискретизатора могут принимать бесчисленное множество значений из ограниченного или неограниченного диапазона 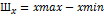 , называемого шкалой сообщения. В результате равномерного квантования с шагом
, называемого шкалой сообщения. В результате равномерного квантования с шагом 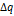 этот диапазон разбивается на конечное число уровней квантования
этот диапазон разбивается на конечное число уровней квантования 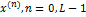 . На рисунке 2б и 2в показана процедура квантования для L=4. На экзамене нужно нарисовать для L=8!
. На рисунке 2б и 2в показана процедура квантования для L=4. На экзамене нужно нарисовать для L=8!
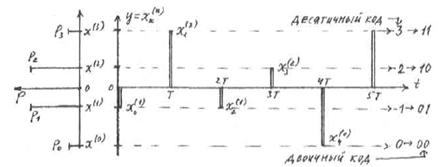
Рис2в.
Шаг квантования можно рассчитать следующим образом:
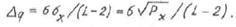
Пороги квантования:
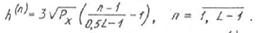
Уровни квантования:
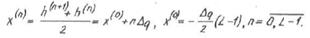
Характеристика квантователя для L=8:
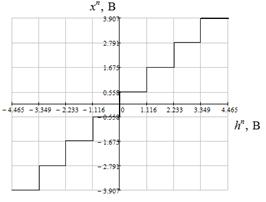
6. ЦАП(вариант \4\):
Цифро-аналоговое преобразование(ЦАП) позволяет на приёмном конце системы связи восстановить непрерывное сообщение 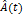 по принятым двоичным комбинациям
по принятым двоичным комбинациям 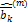 сигнала ИКМ. Это осуществляется с помощью следующих процедур:
сигнала ИКМ. Это осуществляется с помощью следующих процедур:
а) детектирование – восстановления дискретных L-ичных уровней 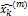 по
по 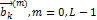
б) интерполяции
в) низкочастотной фильтрации

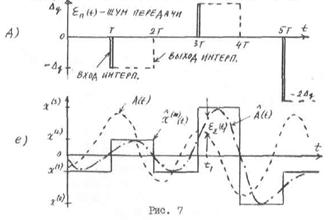
7. Сигналы, спектры на входе и выходе дискретизатора:
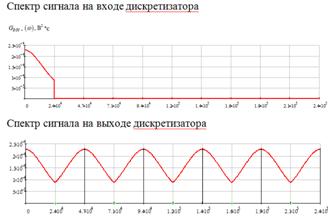
8. Сигналы на входе и выходе квантователя:
Сигнал на входе квантователя:
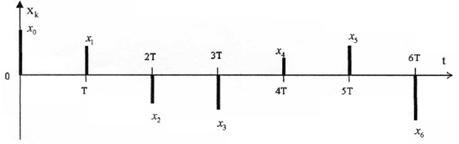
Сигнал на выходе квантователя:

9. Сигналы на входе и выходе восстанавливающего устройства:
10. Модель аналогового АМ сигнала:
Амплиту́дная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда
При АМ амплитуда несущего ВЧ колебания изменяется в соответствии с модулирующим НЧ сигналом.
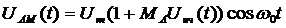 (7.1)
(7.1)
Um - средняя амплитуда АМ сигнала.
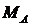 - глубина (коэффициент) АМ.
- глубина (коэффициент) АМ.
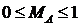
Если модулирующий сигнал гармонический:
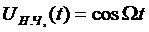
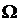 - модулирующая, низкая частота,
- модулирующая, низкая частота,
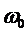 - несущая, высокая частота, то АМ сигнал принимает вид:
- несущая, высокая частота, то АМ сигнал принимает вид:
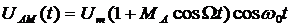 (7.2)
(7.2)
Временная диаграмма НЧ сигнала:
 Uнч(t)
Uнч(t)


 Рис.7.1
Рис.7.1
 |
t
 Временная диаграмма модулированного сигнала АМ:
Временная диаграмма модулированного сигнала АМ:




 uАМ (t)
uАМ (t)
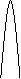 DU
DU
 |
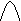 Um t
Um t
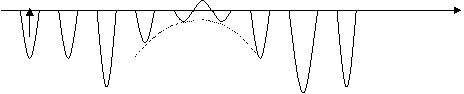



 Рис.7.2
Рис.7.2
В соответствии с временной диаграммой глубина амплитудной модуляции равна:
МA=DU/Um. (7.3).
Определим спектр АМ сигнала, для чего раскроем скобки в выражении для АМ и представим произведение косинусов в виде косинуса суммы и разности углов:
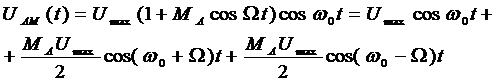 (7.4)
(7.4)
Спектр модулирующего сигнала  .
.
 U
U

Рис.7.3
 W w
W w
Спектр АМ сигнала.
 u Um несущая
u Um несущая
 |
нижняя MAUm MAU m верхняя


 боковая 2 2 боковая
боковая 2 2 боковая
 w0-W w0 w0+W w
w0-W w0 w0+W w
Рис.7.4
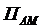 - ширина спектра сигнала АМ – полоса частот, в пределах которой заключена основная доля энергии сигнала.
- ширина спектра сигнала АМ – полоса частот, в пределах которой заключена основная доля энергии сигнала.
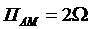 (7.5)
(7.5)
Боковые имеют высоту (амплитуду) не более половины несущей.
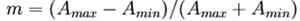 |
11. Модель аналогового ЧМ сигнала:
Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
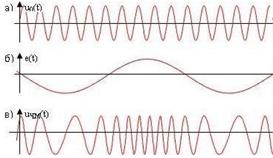
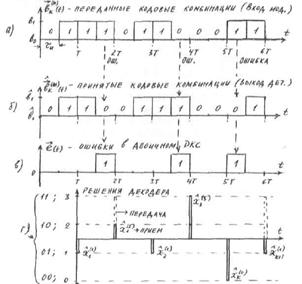
а) — несущая частота, б) модулирующий сигнал, в) результат модуляции
При ЧМ частота ВЧ колебания (несущей) изменяется в соответствии с НЧ модулирующим сигналом.
wчм (t) = w0 + DwUнч(t), где (9.1)
wчм (t)- частота ЧМ сигнала;
w0- среднее значение несущей частоты;
Uнч(t)-модулирующий сигнал;
Dw-девиация частоты, т.е. максимальное отклонение частоты от среднего значения.
Если модулирующий сигнал гармонический, т.е.
Uнч = cosWt,
то wчм(t) = w0 + DwсоsWt
а выражение для ЧМ сигнала имеет вид:
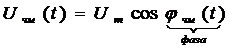
jчм(t) = 
Uчм(t) = Umcos(w0t+ 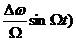
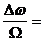 Mч - индекс ЧМ. (9.2)
Mч - индекс ЧМ. (9.2)
Uчм(t) = Umcos(w0t+ 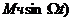
Временная диаграмма модулирующего сигнала имеет вид:
 Uнч(t)
Uнч(t)


 Рис.9.1.
Рис.9.1.
 |
t
Временная диаграмма соответствующего ЧМ сигнала принимает вид:
Uчм(t) 





Рис.9. 
t 
Как видно из рис.9.2, там, где модулирующий сигнал больше, там и частота ЧМ сигнала больше, а период колебаний меньше.
wчм(t) = w0 + DwcosWt
wmax = w0 + Dw
wmin = w0 - Dw
Амплитуда при ЧМ постоянна, меняется только частота.
Для получения спектра ЧМ сигнала разложим Uчм(t) в ряд Фурье.
Uчм(t) = Umcos(w0t+ 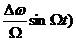 = UmÁ0(Mч)cosw0t+ UmÁ1(Mч)cos(w0+W)t- UmÁ1(Mч)cos(w0W)t+UmÁ2(Mч)cos(w0+2W)t+UmÁ2(Mч)cos(w02W)t+UmÁ3(Mч)*cos(w0+3W)t- UmÁ3(Mч)cos(w0-3W)t+¼
= UmÁ0(Mч)cosw0t+ UmÁ1(Mч)cos(w0+W)t- UmÁ1(Mч)cos(w0W)t+UmÁ2(Mч)cos(w0+2W)t+UmÁ2(Mч)cos(w02W)t+UmÁ3(Mч)*cos(w0+3W)t- UmÁ3(Mч)cos(w0-3W)t+¼
Ák(Mч) - функция Бесселя к-ого порядка.
Вид спектра зависит от Мч.
Спектр ЧМ сигнала при Мч<<1 (т.е. порядка 0,1; 0,05;¼)
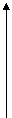
 u Um несущая
u Um несущая
 |
нижняя MчUm MчU m верхняя

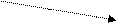 боковая 2 2 боковая
боковая 2 2 боковая
 |  | ||||
 |
 w0-W w0 w0+W w
w0-W w0 w0+W w
Рис.9.3.
При Мч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых), но для ЧМ этот спектр приближенный. Все остальные боковые тоже есть, но они очень малы.
Спектр ЧМ сигнала при Мч>1 выглядит так (Мч=5):
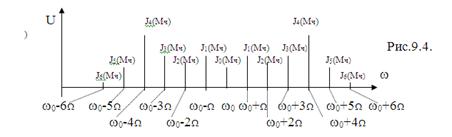
Полоса частот сигнала ЧМ.
Пчм @ 2W(Мч+1)
Мч<<1 Пчм @ 2W, (как при АМ)
Мч>>1 Пчм @ 2WМч = 2W 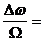 2Dw
2Dw
Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это широкополосный сигнал.
Основные преимущества ЧМ, перед АМ — энергоэффективность и помехоустойчивость.
12. Модель аналогового ФМ сигнала:
Фа́зовая модуля́ция — один из видов модуляции колебаний, при которой фаза несущего колебания управляется информационным сигналом. Фазомодулированный сигнал 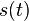 имеет следующий вид:
имеет следующий вид:
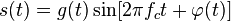 ,
,
где 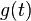 — огибающая сигнала;
— огибающая сигнала; 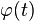 является модулирующим сигналом;
является модулирующим сигналом; 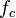 -частота несущего сигнала; t — время.
-частота несущего сигнала; t — время.
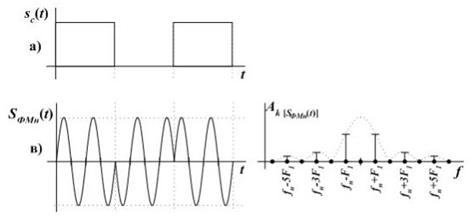
Из спектра можно видеть, почти полное отсутствие несущей, что указывают на высокую энергоэффективность.
Недостаток данной модуляции в том, что ошибка в одном символе, может привести к некорректному приему всех последующих.
13. Параметры задания вашего варианта курсовой работы:
Исходные данные для расчетов приведены в таблице, где 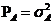 - мощность (дисперсия) сообщения, β – показатель затухания функции корреляции, L – число уровней квантования, G0 – постоянная энергетического спектра шума НКС, h02 – отношение сигнал – шум по мощности на входе детектора, ЧМ – частотная модуляция, НП – некогерентный прием.
- мощность (дисперсия) сообщения, β – показатель затухания функции корреляции, L – число уровней квантования, G0 – постоянная энергетического спектра шума НКС, h02 – отношение сигнал – шум по мощности на входе детектора, ЧМ – частотная модуляция, НП – некогерентный прием.
| ИС; АЦП; L=8 | ПДУ | НКС | ПРУ | Функция корреляции сообщения BA(τ) | |||
| PA, B2 | α, c-1 | Способ передачи | Частота, МГц | G0, Вт.с | h02 | Способ приёма | PAe- β│τ│, β=α.103 |
| f0 | f1 | ||||||
| 1.5 | ЧМ | 1.1 | 1.25 | 0.0010 | 8.5 | НП |
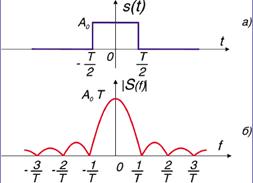
14. Спектр прямоугольного видеоимпульса:
Представление о спектре одиночного импульса можно получить на основе следующих рассуждений. Чем больше период импульсов, тем ближе друг к другу находятся гармонические компоненты в спектре сигнала. Если период стремится к бесконечности, то интервал между частотами составляющих стремится к нулю и спектр превращается в сплошной.
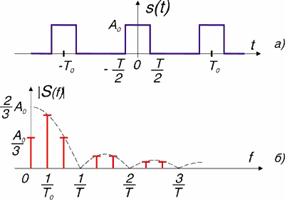
15. Спектр периодической последовательности прямоугольных видеоимпульсов:
Спектр периодической последовательности прямоугольных импульсов имеет сложную структуру. Спектр является дискретным, его компоненты имеют частоты, кратные основной частоте повторения импульсов. В начале координат находится постоянная составляющая последовательности импульсов. Огибающая амплитуд имеет вид функции типа Sinc, точка первого нуля которой располагается на частоте, обратной длительности импульса.
16. Преимущества и недостатки ИКМ:


17. Приём ИКМ методом однократного отсчёта:
Cухоруков 1 часть стр.24-25
18. Регенерация сигнала ИКМ, вероятности P(1/0) и P(0/1):
Под действием помех в канале связи решающее устройство(РУ) может ошибаться. Ошибочные решения бывают двух типов: переход 0 в 1(передавался 0, но РУ выдал 1), характеризующийся условной вероятностью ошибки P(1/0); Переход 1 в 0, характеризующийся условной вероятностью ошибки P(0/1);
Сухоруков 1 часть стр.24-26
19. Вероятность ошибки при регенерации сигнала ИКМ:
20. Оптимальные параметры регенерации ИКМ:
21. Основные характеристики работы ТКС:
22-24. Характеристики ЦФ:
К основным характеристикам ЦФ относятся: импульсная реакция, переходная функция, передаточная функция и связанная с ней амплитудно-частотная и фазочастотная характеристики.
Импульсной реакцией ЦФ 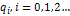 называется отклик
называется отклик 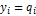 фильтра на входное воздействие в виде единичного импульса:
фильтра на входное воздействие в виде единичного импульса: 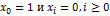 .
.
Переходной функцией ЦФ 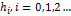 называется отклик
называется отклик 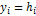 фильтра на входное воздействие в виде дискретной функции единичного скачка:
фильтра на входное воздействие в виде дискретной функции единичного скачка: 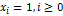 .
.
Переходная функция и импульсная реакция ЦФ связаны соотношением: 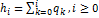 .
.
Передаточная функция ЦФ определяется отношением Z-преобразований отклика и входного воздействия K(Z)=Y(Z)/H(Z), где K(Z), Y(Z), H(Z) – функции комплексной переменной.
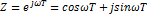 .
.
Связь с временными последовательностями 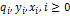 прямым Z-преобразованием
прямым Z-преобразованием 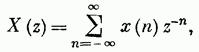
где X(Z) –либо K(Z), Y(Z), X(Z), а x(n) - 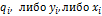 .
.
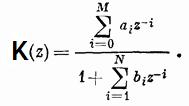 Окончательное ур-е передаточной фун-ии ЦФ.
Окончательное ур-е передаточной фун-ии ЦФ.
Корни числителя – нули передаточной функции. Корни знаменателя – полюса передаточной функции.
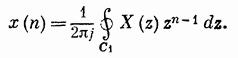 Обратное Z-преобразование.
Обратное Z-преобразование.
Для определения АЧХ и ФЧХ нужно сделать замену: 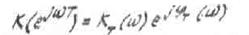
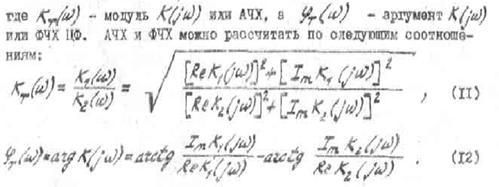
25. Устойчивость ЦФ:

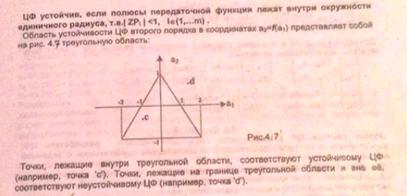
26. Оптимальный приёмник двоичных сигналов:


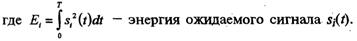

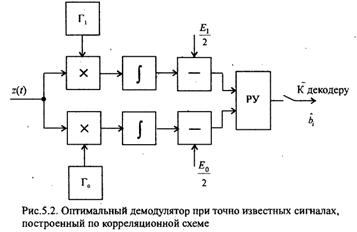
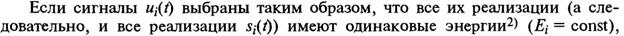
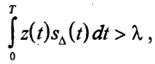

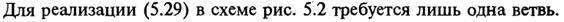

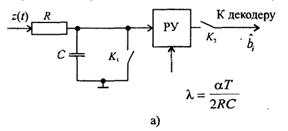

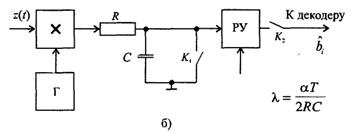
АЛГОРИТМЕ ОПТИМАЛЬНОГО ПРИЁМА(для ознакомления):

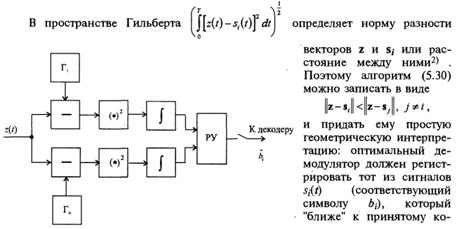

27. Оптимальный корреляционный приёмник:


