Мостиковые схемы
Распространенным частным случаем смешанных соединений (не обязательно резисторов), не сводящихся к набору последовательных и параллельных, являются мостиковые схемы. Принципиально они выглядят так:
Подобные схемы широко используются в различных электроизмерительных устройствах. Например, мостик Уитсона, применяемый для измерения сопротивлений резисторов.
Кусок однородной проволоки (1-2) с достаточно высоким удельным сопротивлением натянут на измерительную линейку, параллельно ей подключают два резистора, сопротивление одного из них Ro известно, сопротивление второго Rx измеряется. К образованной таким образом мостовой схеме подключается источник тока. К точке соединения резисторов А, подключен чувствительный гальванометр, второй вывод которого с помощью скользящего контакта В подключается к проволоке. Передвигая контакт по проволоке, добиваются того, чтобы ток через гальванометр прекратился. В этом случае мост оказывается уравновешенным. Так как сопротивление проволоки пропорционально ее длине, то условие уравновешенности в данном случае имеет вид 
из которого легко определить неизвестное сопротивление, по измерению длин частей проволоки.
В данной схеме электрическое сопротивление измеряется, фактически, с помощью линейки. Помимо простоты данной схемы, ее достоинством является отсутствие необходимости измерять значение силы тока, достаточно убедится в его отсутствии, что может быть сделано с высокой точностью даже не прибором, а индикатором тока. Подобный метод измерения называется «нулевым».
В общем случае, расчет мостиковых схем может оказаться не очень простым из-за большого количества ветвей с разными токами. Если мостиковая схема сбалансирована, то расчет существенно упрощается и проводится с использованием принципа симметрии или приема соединения эквипотенциальных узлов. Для несбалансированных схем всегда остается рутинный и громоздкий метод Кирхгоффа или преобразование звезда-треугольник.
Преобразование звезда-треугольник.
Что такое «преобразованием цепи»? Предположим, у нас есть сложная схема из резисторов, имеющая множество выводов и подключенная к источникам. Заменим эту схему другой, но с тем же числом выводов, причем так, чтобы сопротивления между двумя любыми выводами у новой схемы были такими же, как у старой. Ясно, что источники «ничего не узнают» об этой замене и токи, потребляемые схемой, останутся прежними. Но найти эти токи, возможно, окажется проще.
Итак, если мы хотим подсчитать токи в сложной схеме, ее можно заменить более простой эквивалентной схемой. При этом токи внутри заменяемой части меняются. Поэтому так поступать можно только с той частью схемы, которая нас непосредственно не интересует.
Подобные замены довольно распространены. Пусть, например, в схеме два сопротивлении r 1 и r 2 включены последовательно. Их мы можем заменить одним, равным по величине сумме r 1 + r 2. Если же два сопротивления включены параллельно, то их также можно заменить одним, величина которого равна r 1 r 2/(r 1+ r 2). Это — простейшие примеры преобразования цепей. Остановимся на более сложных схемах.
Посмотрим, как преобразуются друг в друга схемы, имеющие по три вывода, - «звезда» и «треугольник».
Немного непривычные обозначения на рисунке б) очень удобны — индексы показывают, между какими точками включено сопротивление. Например, сопротивление R 13 включено между точками 1 и 3 и т.д.
Если мы хотим заменить одну из этих схем другой, нужно получить такие соотношения между r и R, чтобы сопротивления между любыми точками были для обеих схем одинаковы.
В схеме «звезда» сопротивление между точками 1 и 2 равно r 1 + r 2, а в схеме «треугольник» оно равно R 12(R 13+ R 23)/(R 12+ R 13+ R 23). Следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы
r 1+ r 2= R 12(R 13+ R 23)/(R 12+ R 13+ R 23).
Аналогично, для точек 2 и 3 r 2+ r 3= R 23(R 13+ R 12)/(R 12+ R 13+ R 23), и для точек 1 и 3:
r 1+ r 3= R 13(R 12+ R 23)/(R 12+ R 13+ R 23).
Полученная система легко решается. Сложим все уравнения и поделим обе части на 2: r 1+ r 2+ r 3=(R 12 R 13+ R 12 R 23+ R 13 R 23)/(R 12+ R 13+ R 23).
Вычтя теперь из этого уравнения второе уравнение, получим r 1= R 12 R 13/(R 12+ R 13+ R 23). Аналогично, r 2= R 12 R 23/(R 12+ R 13+ R 23), и r 3= R 13 R 23/(R 12+ R 13+ R 23).
Эти результаты легко запомнить - знаменатель всюду один и тот же, а в числителе справа дважды встречается тот же индекс, что и слева.
Немного сложнее получить формулы для обратного преобразования:
R 12=(r 1 r 2+ r 1 r 3+ r 2 r 3)/ r 3,
R 13=(r 1 r 2+ r 1 r 3+ r 2 r 3)/ r 2,
R 23=(r 1 r 2+ r 1 r 3+ r 2 r 3)/ r 1,
но их также легко запомнить - числитель всюду один и тот же, а в знаменателе стоит как раз тот индекс, которого недостает слева.
Пользуясь данными формулами, можно производить замену одной схемы другой. Например, «звезду» с сопротивлениями 1 Ом можно заменить «треугольником» с сопротивлениями 3 Ом.
Пример:
Найдите сопротивление между точками A и B в схеме на рисунке.
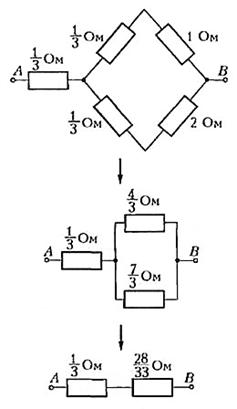Это обычная схема «мостика», но в нашей задаче «мостик» неуравновешен. Заменим «треугольник» ACD «звездой». Теперь ясно, что сопротивление между точками A и B будет равно RAB =1/3+28/33=13/11 Ом.
Мы заменяли «треугольник» ACD «звездой», но можно было решать задачу иначе - заменяя «звезду» ADB «треугольником».
Данный метод очень удобен для последовательного преобразования сложной схемы к простому виду. Он позволяет рассчитать практически любую сложную цепь, состоящую из сопротивлений. Однако его можно применять и к цепям, содержащим не только сопротивления. Обратим внимание на то, что мы вообще не говорили нигде о физических процессах в цепи, а пользовались только формальным выражением для закона Ома: U = rI. Из него следует, что при последовательном соединении сопротивлений их величины складываются, а при параллельном - складываются величины, обратные сопротивлениям. Понятно, что если какие-нибудь другие физические величины связаны законом, аналогичным закону Ома, то все наши выводы справедливы и для них.