| Элемент | λэ∙10-6 ч-1 | Элемент | λэ∙10-6 ч-1 |
| Транзистор V3 (КТ817Б) | 0,035448 | Транзистор V4 (КТ626А) | 0,0616 |
| Резистор R1 (С2-33-0,125) | 0,001344 | Транзистор V6 (КТ315Б) | 0,0287 |
| Резистор R2 (С2-33-0,125) | 0,001276 | Диод V2 (КД509А) | 0,01019 |
| Резистор R3 (С2-33-0,125) | 0,00128 | Конденсатор C1 (К50-35) | 0,00084 |
| Резистор R4 (С2-33-0,125) | 0,001276 | Конденсатор C2 (К50-35) | 0,00084 |
| Резистор R5 (С2-33-0,125) | 0,001276 | Стабилитрон V1 (КС156А) | 0,0049 |
| Резистор R6 (С2-33-0,125) | 0,001285 | Стабилитрон V5 (КС168А) | 0,0049 |
| Резистор R7 (С2-33-0,125) | 0,00093 | Предохранитель плавкий | 0,005 |
| Резистор R8 (С2-33-0,125) | 0,001276 | ||
| Резистор R9 (С2-33-0,125) | 0,001276 |
Составим структурную схему надёжности нашей системы. Поскольку выход из строя 1 элемента влечет за собой выход из строя всей системы, то она состоит из 18 последовательно включенных элементов
Далее рассчитаем надежность стабилизатора напряжения на наработке в 8760 часов (1год). Из теории вероятностей известно, что если определены вероятности появления нескольких независимых случайных событий, то совпадение этих событий определяется как произведение вероятностей их появлений. В нашем случае работоспособное состояние любого из n элементов системы оценивается как вероятность безотказной работы элемента. Система будет находиться в работоспособном состоянии только при условии совпадения работоспособных состояний всех элементов. Таким образом, работоспособность системы оценивается как произведение вероятностей безотказной работы элементов:
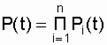
Где Pi(t) - вероятность безотказной работы i-го элемента.
При произвольном законе распределения времени наработки до отказа для каждого из элементов:
|
|
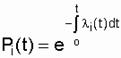
Где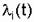 
- интенсивность отказов i-го элемента.
Вероятность безотказной работы системы соответственно запишется:
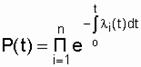
В итоге получаем P(t)=0,99861.
Систему из n последовательно включенных элементов легко заменить эквивалентным элементом, который имеет экспоненциальный закон распределения вероятности безотказной работы. Средняя наработка до отказа системы
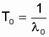, где λ0- интенсивность отказов эквивалента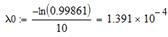 
Таким образом для нашего стабилизатора T0=7189ч.
Резервирование.
1. Общее резервирование с постоянно включенным резервом и с целой кратностью.
Вероятность безотказной работы системы с количеством цепей m + 1 равна
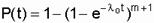
Найдем m при котором вероятность безотказной работы всей системы равно P(t)=0,999.
Для этого необходимо решить уравнение: 1-(1-Pосн)m+1≥0,999
Получаем: m≥0,058 следовательно подходит m=1.
Таким образом средняя наработка до отказа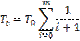 
; Tc=10783ч.
2. Общее резервирование с ненагруженным резервом (замещением) и с целой кратностью.
Вероятность безотказной работы резервированной системы равна
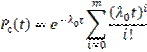
Найдем m при котором вероятность безотказной работы всей системы равно P(t)=0,999.
Для этого необходимо решить уравнение:
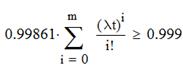
Получаем: m≥1 следовательно подходит m=1.
Таким образом средняя наработка до отказа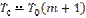 
; Tc=14378ч.
3. Раздельное резервирование с постоянно включенным резервом и с целой кратностью.
Предположим для того чтобы получить вероятность безотказной работы резервированной системы P(t)=0,999 достаточно зарезервировать 1 элемент с максимальной интенсивностью отказа (транзистор V4), проверим это утверждение и найдем степень кратности m.
|
|
Составим структурную схему надёжности резервированной системы и преобразуем ее в удобном виде:
Найдем сначала вероятность безотказной работы P1(t)=0,999149.
Найдем вероятность безотказной работы P2(t) – 1 транзистор основной цепи и m резервных, включенных постоянно. Далее найдем m при котором вероятность безотказной работы зарезервированной системы равно P(t)=P1(t)* P2(t)=0,999.
P1(t)=0.999149; P2(t)=1-(1-e-λt)m+1, где λ- интенсивность отказов транзистора V4.
P1(t)* (1-(1-e-λt)m+1)≥0.999
Получаем: m≥0 следовательно подходит m=1.
Тогда P(t)=P1(t)* P2(t)=0.999149*0.999999971=0.999149=0.999
4.Раздельное резервирование с ненагруженным резервом и с целой кратностью.
Аналогично пункту 3 составим структурную схему надёжности резервированной системы и преобразуем ее в удобном виде:
Найдем вероятность безотказной работы P2(t) - 1транзистор основной цепи и m резервных, включенных постоянно. Далее найдем m при котором вероятность безотказной работы зарезервированной системы равно P(t)=P1(t)* P2(t)=0,999.
P1(t)=0.999149; Pc(t)= P2(t);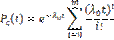 
, где λ0- интенсивность отказов транзистора V4.
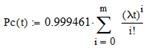
Получаем: m≥1 следовательно подходит m=1.
Тогда P(t)=P1(t)* P2(t)=0.999149*0.99999999=0.999149=0.999